Plant Physiology (Biology 327)  - Dr. Stephen G. Saupe;  College of St. Benedict/ St. John's University;  Biology Department; Collegeville, MN  56321; (320) 363 - 2782; (320) 363 - 3202, fax;    ssaupe@csbsju.edu

Background Information:
   Osmotic potential (Ψ_s) represents the effect of solutes on the energy state of water. Osmotic potential is related to other properties of the solution such as vapor pressure, boiling point, and freezing point. These properties, which are interrelated, are termed colligative properties, and are dependent on the mole fraction of solute. Since these properties are inter-related, one can be measured and used to calculate the others.

    The freezing point of pure water is 0 C but the freezing point of aqueous solutions containing non-volatile dissolved solutes is less than zero. Thus, the addition of solutes depresses the freezing point of water. The extent to which the freezing point is depressed below O C is proportional to the concentration of dissolved solute particles; a 1 molal solution of an ideal non-ionized solute has an osmotic potential of -2.27 MPa and freezes at -1.86 C. Based on this relationship the osmotic potential of any unknown solution can be calculated:  

-2.27 MPa / -1.86 C  =  Ψ_s / Δ_f      rearranging:     Ψ_s = (1.22 MPa deg^-1 ) Δ_f

where Δ_f is the freezing point of the solution in ^oC.

    Since this equation is for solutions at zero ^oC (273 K) we must correct the equation to yield our answer at room temperature by multiplying the equation by the ratio of the absolute temperatures (room temperature in K/273 K). Thus:      

eqn. 1:  Ψ_s = (1.22 MPa deg^-1 ) Δ_f x (room temp in K/273 K)

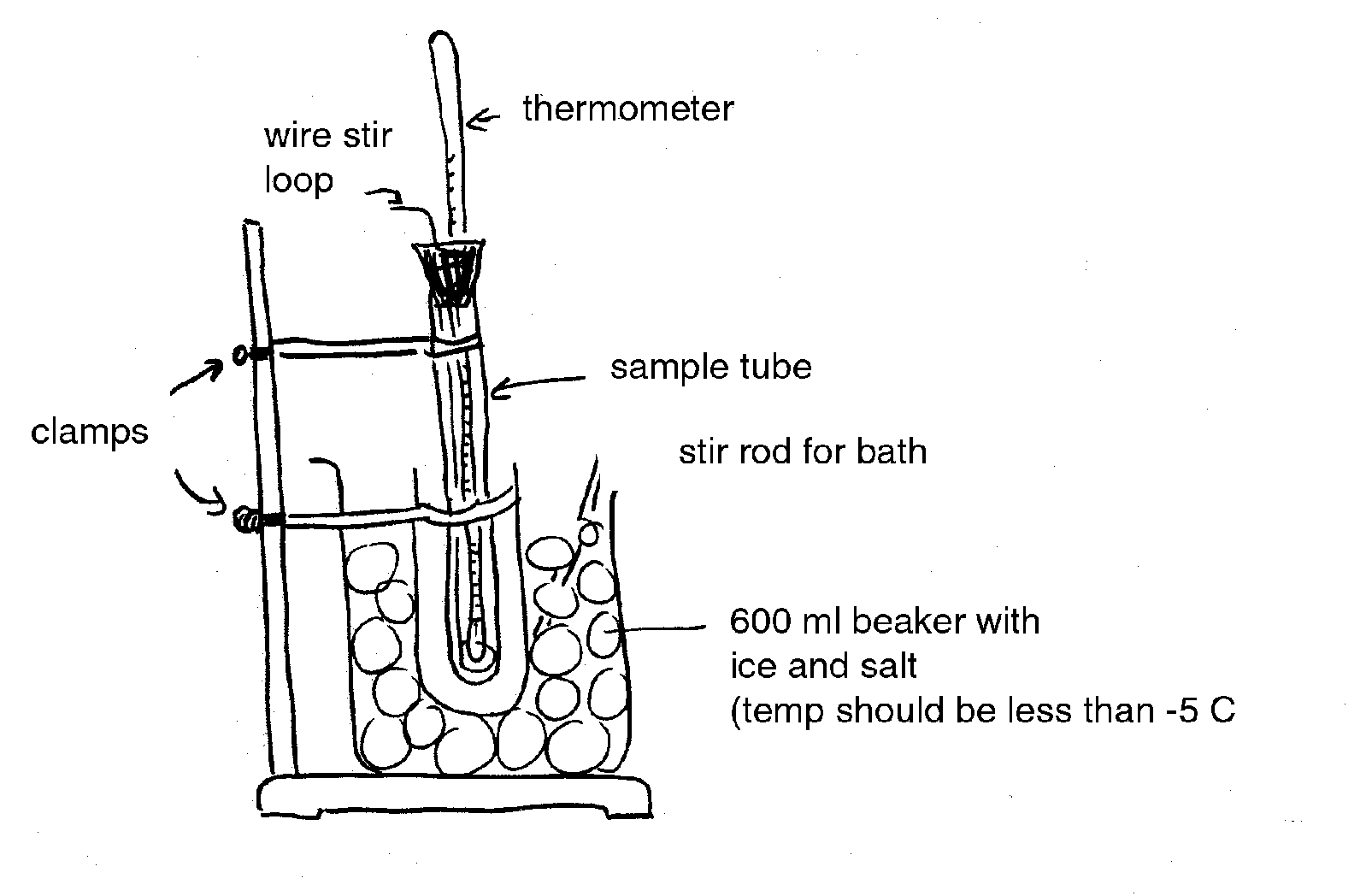
    Freezing point depression is generally determined on tissue sap. Sap samples are prepared by freezing the tissue to rupture cells and then squeezing the frozen material by hand through cheesecloth or with a hydraulic press. Alternately, the tissue can be homogenized (without water) in a blender or with a mortar and pestle.

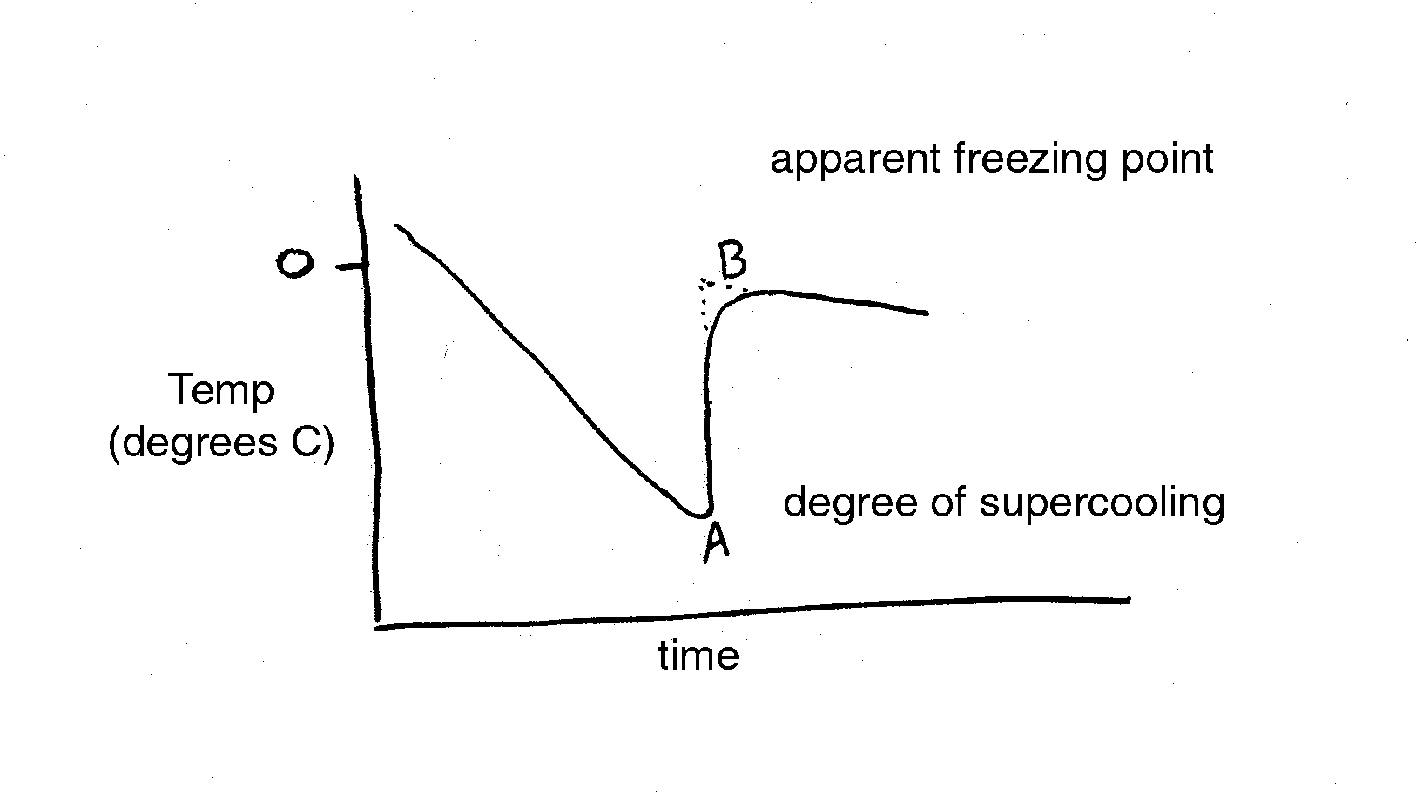
    In practice, the temperature of a sap sample is monitored with a thermocouple or sensitive thermometer as it is cooled. Data from a typical freezing point depression experiment is given below (Figure 1). Point A represents the extent of super-cooling of the solution. The line from A to B represents a very rapid freezing of the water in the solution after super-cooling. The increase is due to the release of the heat of fusion. Therefore, Point B is an estimate of the freezing point depression and is called the apparent freezing point (Δ_f^'). The true freezing point (Δ_f) is obtained after correcting for super-cooling according to the following equation (Reiss, 1996):

eqn. 2: Δ_f = Δ_f^' - 0.0125 � where

Δ_f = true freezing point
Δ_f^' = apparent freezing point
� = degrees of supercooling (negative in sign)
0.0125 = amount of water (1/80) that solidifies per degree of supercooling

    One disadvantage of this method is that the solute composition of the sap influences the accuracy of the measurement. The equation above is given for ideal solutions of glucose or mannitol. Sucrose, on the other hand has a freezing point depression of 2.06^oC, not 1.86^oC. Nevertheless, the method still provides an estimate in reasonable agreement with those obtained by other methods.

Fig. 1.  Typical freezing point curve	Fig 2.  Freezing point apparatus
click here for larger image (tif file format)	click here for larger image (tif file format)

Question: What is the osmotic potential of potato tissue?

Hypothesis: Bland and Tanner (1985) report that the osmotic potential for a potato tube is in the range of -0.58 to -1.53 MPa.  Our tubers should fall within that range.

1. Set up the freezing point apparatus (Figure 2).
   
2. First, we will calibrate the thermometer by placing 3 mL of water in the sample test tube.
   
3. Immerse this unit in a beaker (600 mL) containing salt and ice. The ice bath should be between -5 and -10 ^oC.
   
4. Suspend a thermometer in the sample making sure that it doesn't touch the bottom or sides of the tube.
   
5. Stir the sample continuously and watch the decrease in temperature. When the temperature reaches 0^oC, record the temperature every 10 seconds (Table 1).
   
6. Continue readings as the sap cools. Note the temperature closely. Periodically tap the thermometer gently to induce freezing. When freezing occurs there will be a rapid increase in temperature. Note this temperature which is the apparent freezing point (Δ_f^') and continue to record temperatures until they become fairly constant. [In some cases, the sample may freeze without releasing a detectable heat of fusion. If this occurs, discard the sample and begin again.  You can often determine that this has occurred if there is a plateau in the cooling rate of the sap.] The freezing point of the water should be zero. If the Δ_f^' of the water is not 0^oC, then correct the Δ_f^' of the sap sample accordingly.
   
7. Repeat the experiment with a potato sap sample. To prepare the potato sap, obtain frozen potato sections and carefully remove the peel .  Homogenize the thawed potato in a blender.  Transfer the homogenate to a centrifuge tube and spin at the highest setting for five minutes to recover the supernatant.

1. Complete Tables 1 & 2.
2. Plot temperature vs. time for both sap and water.
3. Calculate the true freezing point (Δ_f) of the sap (Table 2).
4. Calculate the Ψ_s of the sap sample.

Last updated:  01/07/2009     � Copyright  by SG Saupe