
AT5. The Aufbau Process
The quantum mechanical model lets us take an atom and make predictions about its properties. All we need to know is how many protons it has (and how many electrons, which is the same as the number of protons for a neutral atom). We can predict the properties of the atom based on our vague idea of where its electrons are and, more importantly, the energy of those electrons.
How electrons fill in their positions around an atom is called the Aufbau Process (German: "building-up" process). The Aufbau Process is all about keeping electrons at their lowest possible energy.
A corollary of Coulomb's law is that the energy of an electron is affected by attractive and repulsive forces. The closer an electron to the nucleus, the lower its energy. The closer an electron is to another electron, the higher its energy.
Of course, a basic principle of thermodynamics is that a system will proceed to the lowest energy possible. That means, if an atom has only one electron, the electron will have quantum numbers that place it at the lowest possible energy. It will be as close as possible to the positive nucleus.
If an atom has a second electron, it will also be as close as possible to the nucleus. It could have the same quantum numbers as the first electron, except for spin. There is a trade-off, of course, because those two electrons will be close enough to repel each other. However, if it is a choice between that and taking a position much farther from the nucleus, the second electron will go ahead and pair up. These two electrons are sometimes described as being "in the same orbital"; their first three quantum numbers are the same, so that are probably found somewhere in the same region of space. This first orbital, which has no directional restrictions, is called the 1s orbital.

Figure AT5.1. A 1s electron can be found in any direction from the nucleus.
There is only room for one orbital at this distance from the nucleus. A third electron has to occupy another orbital farther away, the 2s orbital. Again, this is a spherical orbital: the electron can be found in any direction. The 2 in 2s means the principle quantum number is two (corresponding to the second general energy level). We sometimes describe this level as being in the second shell, harking back to the Bohr model of the atom. The s in the label "2s" is a code for another quantum number denoting spatial distribution; it means the electron can be found in any direction around the nucleus, just like the 1s electrons.
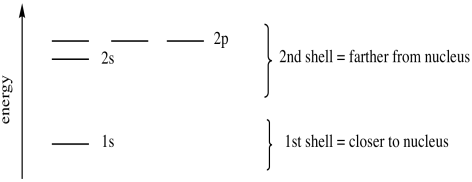
Figure AT5.2. The energy levels of the first and second shell.
The second energy level is large enough to accommodate additional orbitals, but they are a little farther from the nucleus. These are called the 2p orbitals. They are regions of space along the x, y and z axes. There are three orbitals of this type, and they are just called px, py and pz to remind us that they are orthogonal to each other. We sometimes refer to the 2s and 2p energy levels as two different sub-shells within the 2nd shell. Sub-shells are found at slightly different energies from each other, but the energy difference is smaller than the difference from one shell to the next.

Figure AT5.3. A 2px electron is found only in a region of space along the x axis.
The exact direction of the x axis is somewhat arbitrary in chemistry. Mostly it is used in a relative sense: the x axis is perpendicular to the y axis and the z axis. In mathematics, if we are looking at a blackboard or a piece of paper, we often assume the x axis is left-to-right, the y axis is up and down, and the z axis is in and out of the paper or the blackboard. That works if we are thinking about an atom; there is no obvious way to decide which axis points where, so we default to that standard view. Once we start looking at molecules, it is much more convenient to redefine axes in terms of the molecule. For instance, we may designate a particular bond as lying along the z axis. Then the x and the y axes would lie perpendicular to that bond.

Figure AT5.4. A 2pz electron is found only in a region of space along the z axis.
Expressed in a different way, an electron with principle quantum number 2 can have four different combinations of its other quantum numbers. These combinations are denoted 2s, 2px, 2py and 2pz. The three 2p combinations are a little higher in energy than the 2s orbital.

Figure AT5.5. The relative energies of electrons in the first two shells.
Why is the 2p level higher than the 2s level? That's related to the wave behaviour we saw before. With a node in the middle, the 2p orbital behaves as a higher-frequency wave than the 2s orbital. A higher-frequency wave has higher energy. So, a p orbital, with one node, is always higher in energy than an s orbital, with no node.
Once again, we have several energy levels available for an electron, but they will surround the atom in a way that lowers energy. A second electron remains in the lower-energy 1s orbital. It does cost some energy to put two electrons together in the same orbital. This cost is called the pairing energy. You can think of that as an electron-electron repulsion problem, because like charges repel. However, the pairing energy is lowered a little bit if the electrons are spin-paired. In this case, the energy cost to raise an electron to the 2s level is greater than the energy cost to place both electrons together in the 1s level, so the second electron remains in the 1s level.
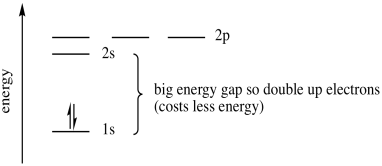
Figure AT5.6. The energetic trade-off between pairing electrons and moving up to the next shell.
A third electron will go into the 2s orbital. It's the lowest in energy. What about a fourth? Does it go into the 2s or a 2p level? Once again the pairing energy is not quite as big as the energy jump up to the 2p orbital. The fourth electron pairs up in the 2s orbital.
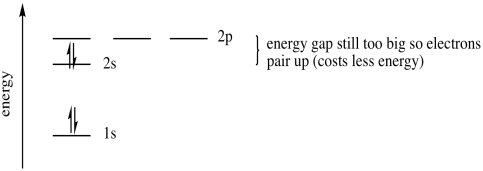
Figure AT5.7. The energetic trade-off between pairing electrons and moving up to the next sub-shell.
A fifth electron goes into one of the 2p orbitals. It doesn't matter which one. We will say it is the px, arbitrarily. A sixth electron again could either pair up in the px, or it could go into the py. But the py energy level is really the same as the px, the electron is just found in a different direction. The energy is the same. That means a sixth electron will go into the py rather than pair up in the px, where it would experience extra repulsion.
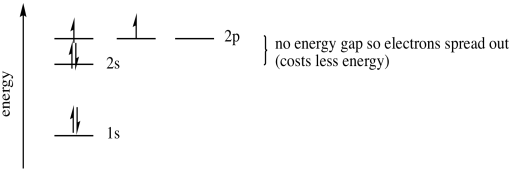
Figure AT5.8. The energetic trade-off between pairing electrons or going into an orbital in the same sub-shell.
This pattern of "filling" electrons is generally followed for all of the elements. The tally of how many electrons are found in each orbital is called the electron configuration. For example, hydrogen has only one electron. Its ground state configuration (that means, assuming the electron hasn't been excited to another orbital via addition of energy) is 1s1.
On the other hand, an atom with six electrons, such as the element carbon, has the configuration 1s22s22px12py1. There is one electron in each of two p orbitals in order to avoid repulsion, which would happen if they were in the same one.
Problem AT5.1.
Write electron configurations for the following elements.
a) oxygen, O
b) sulfur, S
c) silicon, Si
d) nitrogen, N
e) argon, Ar
f) neon, Ne
This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with contributions from other authors as noted. It is freely available for educational use.
 Structure & Reactivity in Organic, Biological and Inorganic Chemistry
by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Structure & Reactivity in Organic, Biological and Inorganic Chemistry
by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
Navigation: