
AT4. Quantum Numbers
On the very, very small scale of the universe, things don't behave exactly as we are used to. Electrons are one example. They are not solid objects. They are waves. Or are they? On the nanoscale, things can be both particles and waves. An individual particle like an electron has mass, but it is spread out, not located in one position, and it has a wavelength.
The recognition of the wave properties of the electron provided a breakthrough in understanding its properties. Schrodinger's wave equation allowed scientists to make predictions about the electronic structure of atoms. Where are the electrons found? What is their energy?
The wavefunction is a mathematical expression that describes the electron. It can be plotted, like a graph, although it is a graph in three dimensions instead of two. The three-dimensional plot of the wavefunction is sometimes called an orbital. Often, chemists find it useful to look at pictures of orbitals in order to gain some sense of where electrons may be and how they may behave. Orbitals are something like the wave form of the electron.
In another sense, orbitals are related to probability maps -- the wavefunction squared reveals the probability of an electron being located at a particular position in space. It might be helpful to picture them that way. Suppose you could take a series of pictures of an electron and superimpose all of those pictures, like time-lapse photography. The result might look something like the drawing below, in which every dot represents where the electron showed up in one of our pictures. It's impossible to predict exactly where the electron would show up in the next picture, but it would be a pretty good guess that it would show up somewhere in the same rough circle as it did all of the other times.

Figure AT4.1. A 1s electron "orbital".
Of course, in three-dimensional space, we would be looking at a sphere instead of a circle. Maybe our picture is just a thin slice through the middle of that sphere. In the very center of the sphere, we would find the nucleus of the atom. So this electron is found within a certain distance of the nucleus, but it can be found in any direction. We call an electron that behaves this way an s electron. This spherical region of space in which the electron is likely to be found is called an s orbital.
The drawing above is labelled 1s, specifically. An atom can have many s electrons, but this is the one that is closest to the nucleus. It is the first s electron we would encounter if we started at the nucleus and moved outward through the atom.
Other electrons have different distributions about the atom. They are more likely to be located in different places. In solving the Schrodinger wave equation, it turns out that there are four variables that must be restricted to certain values if the equation is to have a sensible solution. The values of these variables determine where the electron is likely to be found around the atom, and roughly how much energy it will have.
The four quantum numbers are given the symbols n, m, l, and s. If you need to, you might remember that via the word aNiMaLS. Each quantum number tells you something different about the electron that it describes. The first one, n, tells you about distance. This number has to be an integer, so it could be 1, 2, 3, 4,... How far is the electron from the nucleus? If n = 1, the electron is as close to the nucleus as it could be; if n = 4, it is further away.
We sometimes think of n as describing the "shell" of the atom. Think of the old Bohr model of the atom, with electrons being found at different distances from the nucleus. It's like the atom is a set of Russian nested dolls, with one shell outside another. The first shell (n = 1) is close to the nucleus, the second (n = 2) is farther out, and so on.
The second number, m, tells you about spatial distribution, or shape. Maybe we know how close the electron is to the nucleus, but can it be found anywhere within a certain distance, or only in certain directions? This number has to be an integer, and it has to be less than n. If n = 1, m = 0. If m = 0, there is no "shape" preference, and the orbital is spherical. These numbers describe our 1s orbital, above.
The third number, l, can be a positive or a negative integer. It can be anywhere from +m to -m. If n = 1, and m = 0, then l = 0, too. The number l roughly correlates to orientation: in what direction is the orbital oriented? If there is only one possible value of l, then there must be only one possible orientation. That's true for something spherical; it doesn't matter which direction you look at it, because it will always look the same.
The final number is s. That's the spin quantum number and it can have only two values, regardless of the values of the other quantum numbers. It is either +1/2 or -1/2. Spin doesn't have a very tangible explanation in the macroscopic world, but if electrons have opposite spin values then they can occupy the same orbital. Thus, one pair of electrons can be described by each orbital.
Every electron in an atom must have a unique set of quantum number. If n, m, and l are the same for two electrons, then s must be different.
What happens when n = 2? In that case, the electron could be farther from the nucleus. The orbital will be bigger. In this case, m could either equal 0 again, or it could equal 1. If m = 0, like in the case of the 1s orbital, the orbital will be spherical. It will be a 2s orbital. Of course, l = 0, too, because l can only range from +m to -m. This orbital will be spherical, too, because m = 0. It will look just like a 1s orbital, only bigger.
However, if we could look at a thin slice through the orbital, we would see a difference between a 1s and a 2s orbital. The 1s orbital is uniform throughout, but the 2s orbital has a phase change. Remember, it is a wave, and it has peaks and troughs. This is a three-dimensional, spherical wave, but it has a trough nested inside and the peak is on the outside (or vice versa).

Figure AT4.2. A slice through spherical 1s orbital and 2s orbitals.
If we go further from the nucleus, we may encounter a 3s orbital and a 4s orbital. These, too, would look like bigger 1s orbitals from the outside. However, a thin slice through the middle would reveal the phase behaviour of the orbital, with peaks and troughs alternating from the centre to the edge.

Figure AT4.3. Slices through a series of spherical s orbitals.
But let's step back for a moment. If n = 2, then m = 0 or 1, because m can be any integer less than n. We looked at the case in which m = 0; that's an s orbital. What if m = 1? The quantum number m describes the number of nodal planes that slice through the centre of an orbital. If m = 1, we would take the regular s orbital and chop it through the middle (or loop a rope around the middle and tie it tight) to get two different halves. These halves would be out of phase with each other. This type of orbital is called a p orbital. It has two lobes. On lobe is on one side of the nucleus and the other lobe is on the other side of the nucleus.

Figure AT4.4. A p orbital.
If m = 1, then l = 1, 0, or -1. That means this p orbital could be oriented in any of three directions. Since we are really talking about three different electrons, and they would repel each other, then they will get as far as possible from each other. The easiest way to do that, if you can imagine x, y, and z axes meeting at the nucleus, is to have one p orbital pointing along the x axis, one along the y axis, and one along the z axis. These three p orbitals are called 2px, 2py, and 2pz.
Just like with the s orbital, we could also have p orbitals farther from the nucleus. We can't have one closer to the nucleus; there isn't enough room closer in to the nucleus, and the quantum rules prevent a p orbital at energy level n = 1. A 3p orbital would look just like a 2p orbital, and could lie in three different directions. However, if we could take a thin slice through its middle and pull it out, we could see the same internal phase changes that we saw in the 2s, 3s, and 4s orbitals.

Figure AT4.5. A slice through a 3p orbital.
So we can have one spherical s orbital at energy level 1, another spherical s orbital at energy level two, and three propellor-shaped or dumbell-shaped p orbitals at energy level 2. What about energy level 3? If n = 3, then m = 0, 1, or 2. That means there is a third shape possible at this level. To see the shape, we would take a p orbital and pinch it in half again, but in a direction perpendicular to the one we chose the first time. This would result in a cloverleaf shape. This is called a d orbital. There would be five different orientations of a d orbital, because l = 2, 1, 0, -1, or -2.

Figure AT4.6. A slice through a 3d orbital.
The d orbitals can point their lobes between the axes: the dxy has lobes in the xy plane but between the x and y axes; the dyz is in the yz plane with lobes between the y and z axes; the dxz is in the xz plane and its lobes point between the x and z axes. The two remaining d orbitals point along the axees. The dx2-y2 orbital points the lobes of its cloverleaf along the x and y axes. The dz2 orbital is not a clover shape like the others; it looks like a p orbital emerging from a donut. The two lobes extend along the z axis, and the donut (usually called the toroid) sits in the xy plane.
We could go one step further, although you are not likely to encounter the next level (many students only need to work with s and p orbitals). If n = 4, we could have s, p, or d orbitals for the values of m that we have seen before, but if m = 3, then we will have to chop the d orbital shape into additional lobes again, producing a funky f orbital. There are actually several ways this happens, producing several different shapes; only one is illustrated below. An f orbital can have seven possible orientations.

Figure AT4.7. An f orbital.
More commonly, the overall shapes of these orbitals are depicted in "cartoon" form. For example, an s orbital is usually just shown as a ball or sphere. Drawing things this way can be a little misleading, because the orbital looks like a solid object, rather than a general area of space where an electron might be found. These cartoons offer the advantage that they are a simple way of indicating where various electrons may be found in an atom.

Figure AT4.8. The common depiction of an s orbital.
The three p orbitals are shown here. Each one is a dumbell shape pointing in a different direction along Cartesian coordinates (x, y, z).

Figure AT4.9. The common depiction of the p orbitals.
There are five d orbitals. Four of them are cloverleaf shapes, but the fifth contains a toroid (or donut shape).
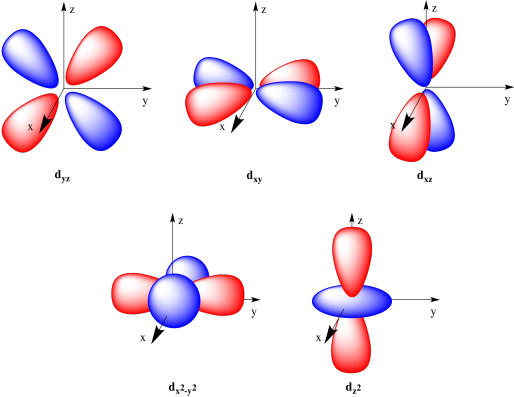
Figure AT4.10. The common depiction of the d orbitals.
The seven f orbitals are shown below. Four of them look like orange segments, lying on one plane. Two of them look like the cloverleaf d orbitals that have split into two layers. The last one is like the dz2 orbital, only it has two toroids instead of one. Don't freak out; most chemistry classes don't work much with lanthanides and actinides so you might never see these orbitals again.

Figure AT4.11. The common depiction of the f orbitals.
Note that these orbitals can be drawn in different ways. For example, p orbitals are usually drawn in a way that shows that they have phase. Either the two lobes are coloured differently to show that they are out of phase with each other, or they are shown with one lobe shaded and the other left blank.
![]()
Figure AT5.4. The 2px orbital shown with phase information.
We can summarize quantum numbers in a couple of ways. Remember, quantum numbers are just variables in the Schrodinger wave equation that have to take certain values in order for the equation to have a sensible solution. These values are usually integers, and they depend on each other. There is something different about the quantum numbers that describe each electron in an atom; in part, that helps to keep the electrons away from each other.
Table AT5.1. Possible ranges of the four quantum numbers.
| number | n | m | l | s |
| rules | integer | less than n | -m to +m | 1/2 or -1/2 |
For example, the 1s electrons on a helium atom have to be different from each other somehow. They have the same values of n, m, and l, so s is different.
Table AT5.2. Possible values of the four quantum numbers if n = 1.
| number | n | m | l | s |
| rules | integer | less than n | -m to +m | 1/2 or -1/2 |
| 1st set (1s) | 1 | 0 | 0 | 1/2 |
| 1 | 0 | 0 | -1/2 |
As we proceed to the second "shell" of electrons around the atom, m can vary, and so can l. That means we get different shapes and orientations of the allowed waves for the electron. We'll ignore s in the following table; in each case, there are two possibilities, s = 1/2 and s = -1/2; two electrons can be described by each orbital.
Table AT5.3. Possible values of the four quantum numbers if n = 1 or 2, along with spatial descriptions of the orbitals.
| number | n | m | l | orbital description |
| rules | integer | less than n | -m to +m | |
| 1st set (1s) | 1 | 0 | 0 | spherical |
| 2nd set (2s) | 2 | 0 | 0 | spherical |
| 3rd set (2p) | 2 | 1 | -1 | dumbbell (orthogonal directions) |
| 2 | 1 | 0 | ||
| 2 | 1 | -1 |
When we get to the 3rd shell, there are even more variations.
Table AT5.4. Possible values of the four quantum numbers if n = 1 to 3, along with spatial descriptions of the orbitals.
| number | n | m | l | orbital description |
| rules | integer | less than n | -m to +m | |
| 4th set (3s) | 3 | 0 | 0 | spherical |
| 5th set (3p) | 3 | 1 | -1 | dumbbell |
| 3 | 1 | 0 | ||
| 3 | 1 | 1 | ||
| 6th set (3d) | 3 | 2 | -2 | cloverleaf |
| 3 | 2 | -1 | ||
| 3 | 2 | 0 | ||
| 3 | 2 | 1 | ||
| 3 | 2 | 2 |
Overall, the quantum number n indicates the shell in which an electron is found. That is, it indicates distance from the nucleus.
In addition, n can also indicate the number of spherical nodes in an orbital. As we saw in the progression of s orbitals, each type of orbital (s, p, d, f) becomes "nested" when we move to higher levels; a 2s orbital is like a 1s orbital nested inside a bigger, spherical shell, with a spherical node in between the two parts. A 3s orbital contains one more spherical node (two total), and so on.
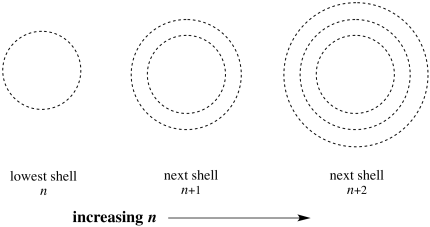
Figure AT4.12. The number of spherical nodes increases with each shell.
Quantum number m indicates the shape of the orbital. Is the orbital divided into different lobes? Described in a different way, it indicates how many nodes or nodal planes there are between these lobes. An s orbital is completley shpherical, with no lobes. A p orbital has a nodal plane cutting it in half, forming two lobes. A d orbital has two nodal planes, usually resulting in four lobes, and so on.
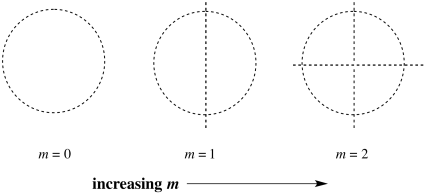
Figure AT4.13. The number of planar nodes increases with quantum number m.
If the orbital does have a non-spherical shape, l corresponds to different directions in which it can be oriented. Of course, s is the spin, and two electrons in the same orbital have to have opposite spins.
Problem AT4.1.
Provide labels (e.g. 1s, 3p, etc) for the following orbital descriptions.
a) a spherical orbital in the second shell of the atom.
b) a dumbbell-shaped orbital in the third shell of the atom.
c) a cloverleaf-shaped orbital in the third shell of the atom.
d) an orange-slice shaped orbital in the fifth shell of the atom.
e) an orbital that looks like one ball nested inside a second ball netsed inside a third ball
Problem AT4.2.
Draw cartoons of the following orbitals.
a) a 4p orbital.
b) a 4d orbital
c) a 5d orbital
d) a 6f orbital
Problem AT4.3.
As we go to higher shells in the atom, we start to see additional spherical nodes in the orbitals. Make a sketch of each orbital below, and superimpose a repeating sine wave over the drawing such that the nodes in the sine wave correspond to the nodes in the orbital.
a) a 2p orbital
b) a 3p orbital
c) a 4p orbital
What happens to the number of sine wavelengths as we go from one shell to the next?
This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with contributions from other authors as noted. It is freely available for educational use.
 Structure & Reactivity in Organic, Biological and Inorganic Chemistry
by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Structure & Reactivity in Organic, Biological and Inorganic Chemistry
by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
Navigation: