There are a many ways we can use NMR spectroscopy to analyse compounds. One common application is in determination of an unknown structure. Given the MS, IR, ¹³C and ¹H NMR spectra, what might be the structure of an unknown sample?

It is often easiest to start with the IR spectrum.

• identify at least three peaks in the IR spectrum. Which peaks seem to tell you the most information about this compound?
• don't think with your head; think with your hands. Write down ideas on the spectrum.
• if you are working on a formal proof of structure, on a class test or a lab report, you may be required to enter your data in a table correlating wavenumber with peak assignment:

Table NMR13.1. An IR data table waiting to be filled in.

For example, a student might obtain the following IR spectrum.

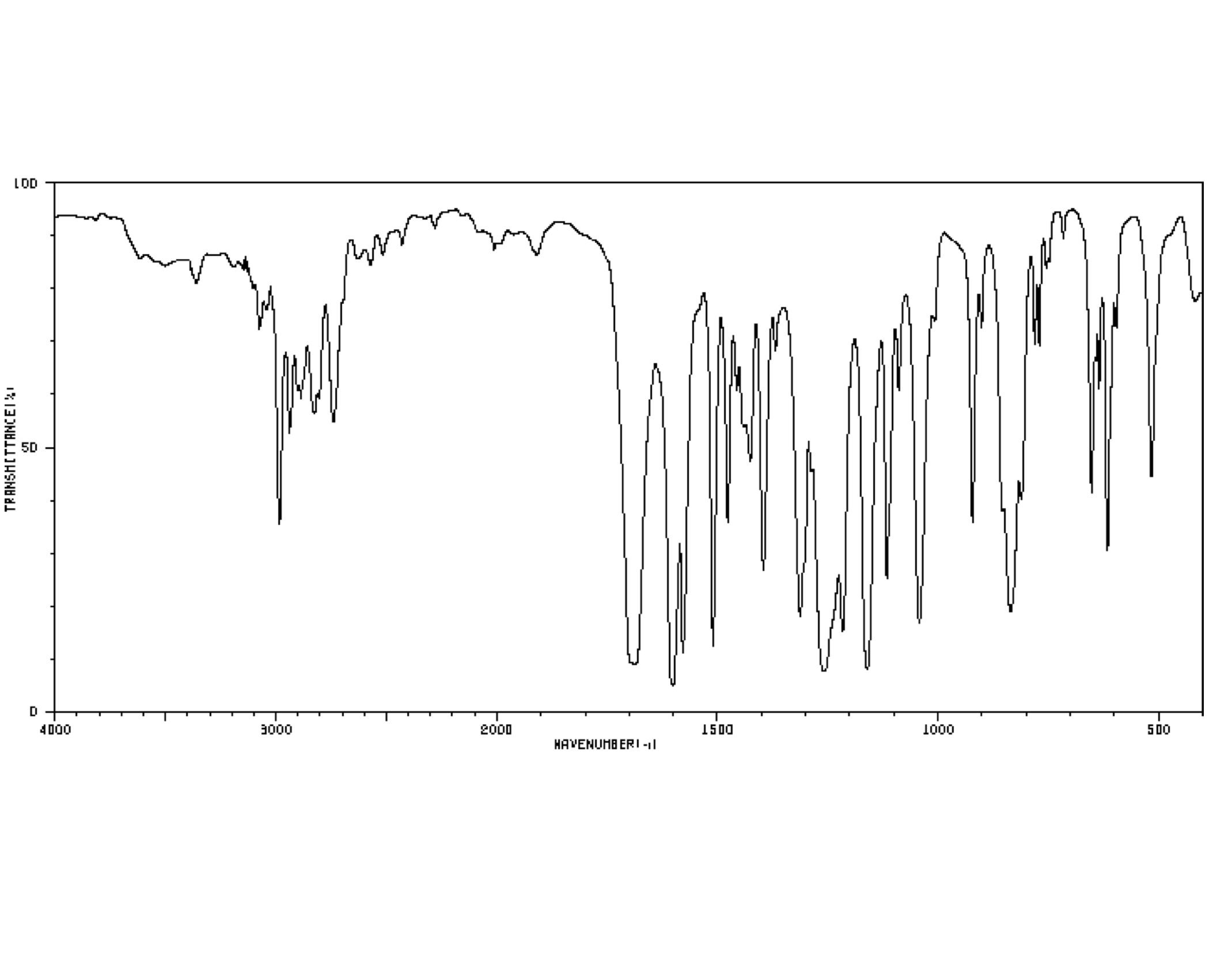
Figure NMR13.1. An infrared spectrum of an unknown sample.¹

From that information, she constructs the following table.  She might even write this table, by hand, directly on her spectrum.  She makes useful notes on the edges, and might even include some guesses, which she later crosses out, but does not erase.  She is assisted in this task by consulting an IR table, that suggests what some of these peaks might mean.

Table NMR13.2. An IR data table for an unknown sample.

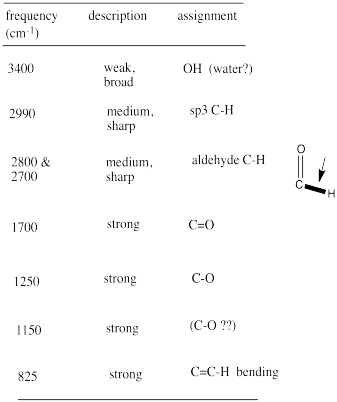
Remember:

• make special note of what atoms are present in the compound: C, H, N, O...
• also note your initial ideas about specific functional groups that may be present.
• if you are unsure of an assignment, put a question mark beside it to signal this uncertainty.
• some data may need to be discarded later if it is not consistent with other data.

Look at the ¹³C spectrum.

• How many different carbons are there, based on the number of peaks in the spectrum? This is the first step in estimating the molecular formula.
• Do you have reason to believe there is symmetry in the structure? In the entire compound or just part of it? Adjust the number of carbons you think you are dealing with.
• As in IR spectroscopy, begin assigning peaks, either on the spectrum or, if required, in a table:

Table NMR13.3. A ¹³C NMR data table waiting to be filled in.

For example, a student might obtain the following ¹³C NMR spectrum:

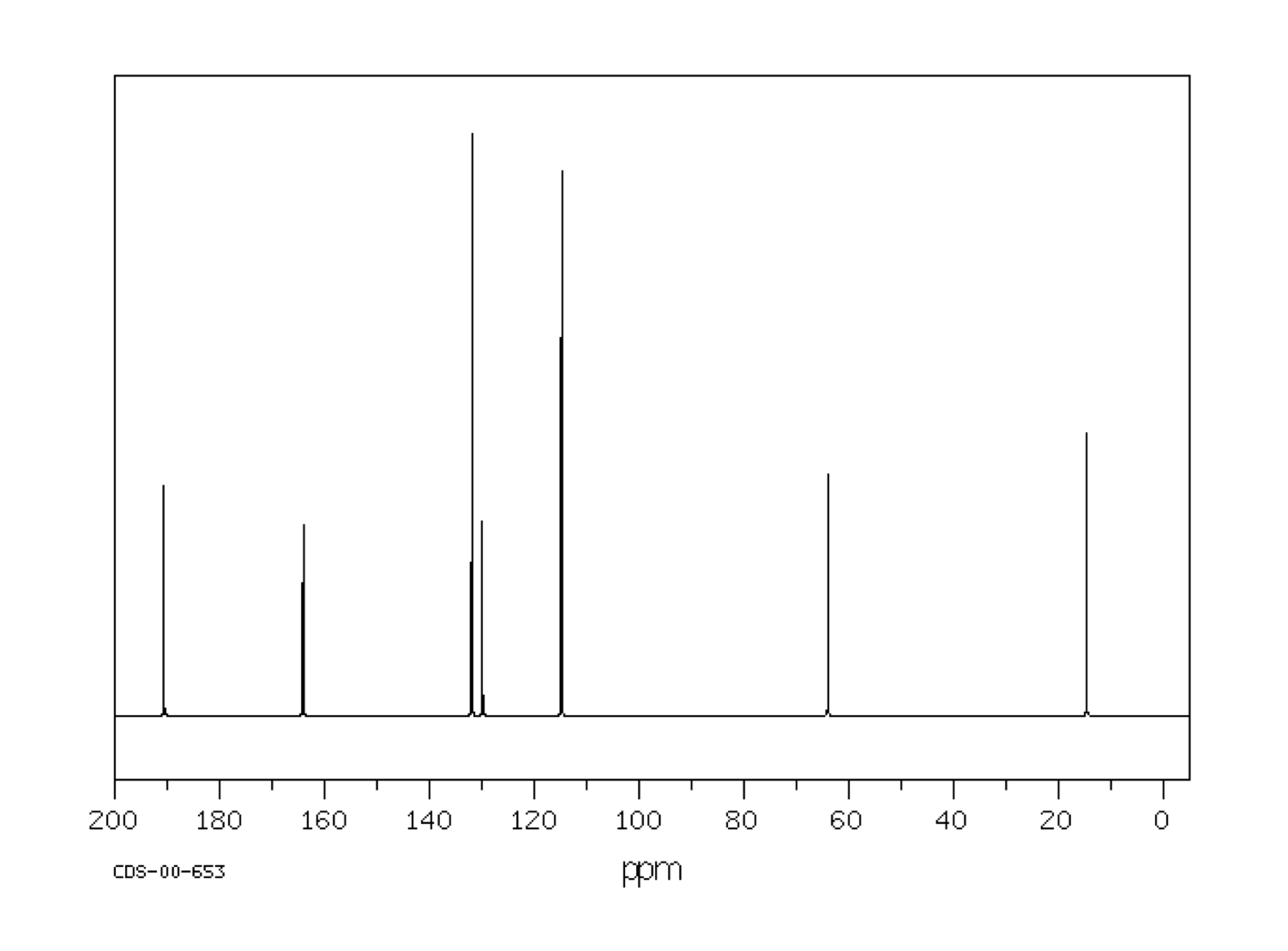
Figure NMR13.2. A ¹³C NMR spectrum of an unknown sample.¹

From that information, she puts together the following table: 

Table NMR13.4. A ¹³C NMR data table for an unknown sample.

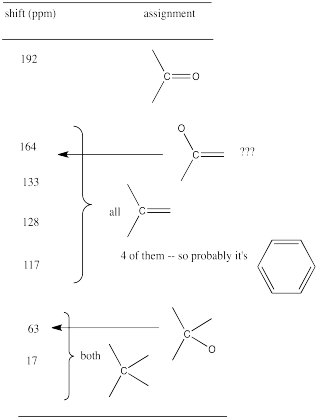
Remember:

• you will be able to assign all peaks in the NMR spectrum, not just a few like in IR.

As in ¹³C NMR, you should be able to assign all peaks in the ¹H NMR spectrum. You may be able to do so by making notes on the spectrum. If you think you know the structure, you may be able to draw it and note which peak belongs with which proton.

A formal proof of structure might require a table of assignments.

Table NMR13.5. A ¹H NMR data table waiting to be filled in.

• This table demonstrates your ability to read the spectrum. Can you decide what ratio of protons is suggested by the integral line? Can you decide whether a peak is a quartet?
• The partial structure column should explain the shift, integration and multiplicity for the peak in that row. It should not show any other information from elsewhere in the structure. This restriction forces you to demonstrate a thorough understanding of the data in a way that "getting the right answer" does not.
• The partial structure column is best filled in with drawings, not words. The drawing is a partial structure.
• Because the partial structure will show the protons absorbing at the shift in that row as well the neighbouring protons, you need to distinguish between them in your picture. Most people circle or underline or make bold the protons that show up at the shift given in that row.
• When finished with the partial structure column, you should be able to link the partial structures together to make an entire structure in the assignment column.

An example of a spectrum and its accompanying data table is given below.  Here is the spectrum:

Figure NMR13.3. A ¹H NMR spectrum of an unknown sample.¹

Here is a data table:

Table NMR13.6. A ¹H NMR idata tablee for an unknown sample.

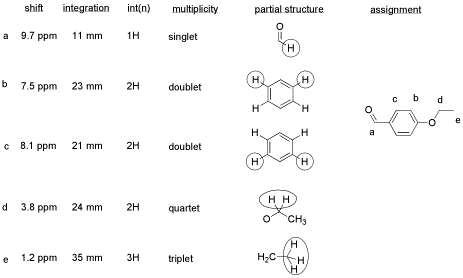
Things to note:

• This student has used two integration columns instead of just one. 
• The first column shows the integral measured from the spectrum.  She probably used a ruler.
• The second column, which she called int(n), contains a convenient ratio taken from the raw data.  The (n) stands for normalized.  This ratio is easier to use in her assignments.
• Also note that the peak at 9.7 ppm does not have a very good integral.  There is either a "phasing" or a "level & tilt" problem here that can be corrected using the NMR software, but this is sometimes difficult to do.  If she had taken an automatic printout of this integral measurement, she would have gotten a strange number; in this case, it would be about -5, because the end of the integral line is lower than the start.  It clearly isn't a negative number of hydrogens, though.  She has instead measured the vertical rise in the integral and recorded that; it isn't perfect, but is a fair estimate in this case.

There are a couple of additional tools that can help to confirm the structure at this point.  Alternatively, if the structure is still elusive, these tools might help to produce some ideas.

The first tool is the formula.  Once we have NMR tables, we can begin guessing at the numbers of carbons and hydrogens in the structure.  With the addition of an IR table, we can begin guessing at the presence of other atoms, such as oxygen or maybe nitrogen.

For example, in the ¹³C NMR table above, there were seven peaks.  That means there are probably at least seven carbons.  We can start off the molecular formula as C₇.  However, there may be additional carbons if there is some symmetry.  There may also be a few carbons that do not show up very well in the spectrum.  If you have ever obtained a real ¹³C NMR spectrum, you will know that carbonyl peaks can be hard to find, especially if there are no hydrogens attached to the carbonyl.  In the table above, it looked like there was a benzene, so maybe there werereally six carbons in the aromatic region, and not just four carbons.  That would mean the formula, so far, is C₉.

In the ¹H NMR table, the integrals added up to a total of 10H.  So, maybe the formula is C₉H₁₀.

Furthermore, the IR table suggested the possible presence of two different oxygen atoms.  The formula may actually be C₉H₁₀O₂.

Once we have a formula, we actually get a great deal of information automatically.  One of the most important pieces is "units of unsaturation" or "degrees of unsaturation" (DU).  The DU is the result of a formal comparison of the C/H ratio in the compound to that in a normal alkane.  In a normal alkane, the formula is always C_nH_2n+2.  If you picture a long hydrocarbon chain, there will be two hydrogens on each carbon along the chain, plus one more hydrogen at either end of the chain.  However, an alkene contains one pi bond, and at the site of that pi bond there are two hydrogen atoms missing from that alkane formula.  A simple alkene always has the formula C_nH_2n.  That missing pair of hydrogens in the formula is called a degree of unsturation.

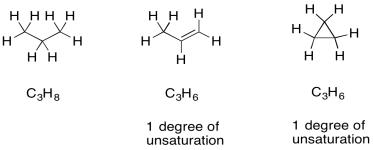
Figure NMR13.4. Examples of degrees of unsaturation in hydrocarbons.

The same thing also happens to the formula if there is a ring present.  One DU can correspond to the presence of a double bond or a ring.  If DU=2, there may be two double bonds, two rings, or one of each.

If there are oxygen atoms present in the formula, we can just ignore them and pay attention to the hydrocarbon part.  Conceptually, because oxygen forms two bonds, we can think of it as squeezing in between any two atoms in a hydrocarbon structure to form a new compound.  The ratio of carbon to hydrogen is unchanged.  If there is a degree of unsturation in a formula containing oxygen, it simply suggests the presence of a ring or a double bond, just like in a hydrocarbon.

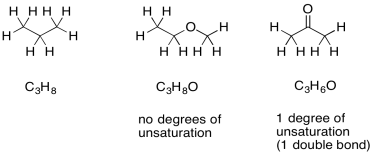
Figure NMR13.5. Examples of degrees of unsaturation in oxygen-containing compounds.

Sometimes, if there are other atoms present, we need to adjust the formula to take them into account.  For example, any time a halogen is found in the structure, it conceptually replaces a hydrogen atom.  In order for a halogen to be found in the structure, there would have to be one fewer hydrogen atoms in order to open up a spot for the halogen.  To adjust for the presence of a halogen, we need to add one hydrogen into the formula, then compare it to the standard alkane formula.

Figure NMR13.6. Examples of degrees of unsaturation in amines and haloalkanes.

Nitrogen, on the other hand, has three bonds.  Unlike oxygen, if we squeeze it in between two other atoms, it still needs one extra bond.  It always brings an extra hydrogen into the formula.  To adjust for the presence of nitrogen, we need to subtract one H from the formula, then compare it to the standard alkane formula.

In the formula we just calculated, we have C₉H₁₀O₂.  We can ignore the oxygens and look at the C9H10.  If this were a saturated hydrocarbon with nine carbons, its formula would be C₉H₂₀ (since 2 x 9 + 2 = 20).  We are missing five pairs of hydrogens, so DU = 5.  That is a lot.  However, if we have one benzene in the structure, that would account for three double bonds and one ring all at once.  That four degrees of unsaturation.  An additional carbonyl would bring the number up to the required five.  If we had not yet arrived at the idea of a benzene ring, this comparison might make us think of it.  Alternatively, if we knew about the benzene but hadn't yet spotted the carbonyl, we might be on the lookout for it now.

Once we have a possible formula, another useful tool is mass spectrometry (MS).  Even if you don't know much about mass spectrometry, the basic idea is simple.  A mass spectrometer takes a molecules and bashes it into little pieces, then measures the molecular weights of each of those fragments.  If you are lucky when you run the experiment, some of the molecules are left intact, and you get the molecular weight of the entire molecule, too.

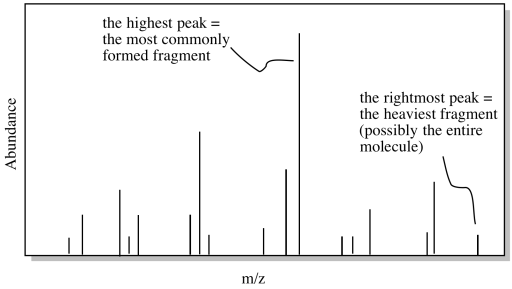
Figure NMR13.7. A cartoon of a mass spectrum.

If we calculate the molecular weight based on the formula and compare it to the possible molecular weight from the mass spectrum, we might get confirmation that we are on the right track.  Alternatively, maybe our calculated molecular weight will come up short.  If we are off by 16, maybe we have missed an oxygen atom somewhere.  If we are off by 14, maybe we have missed a carbon and a pair of hydrogens.  This information might help us to correct some mistakes.

In the above example, the formula leads to a molecular weight of 150 g/mol.  If the mass spectrum did not match, we would want to check our work to see if we overlooked something.

Problem NMR13.1. 

Using the approach outlined above, build a case for the structure of the compound represented by the data below.

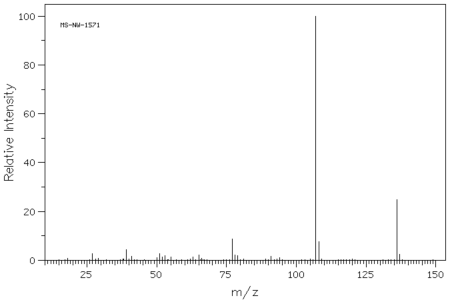
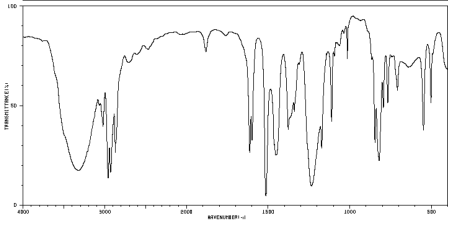
Problem NMR13.2.

Using the approach outlined above, build a case for the structure of the compound represented by the simulated data below.