Reactivity in Chemistry
Photochemical Reactions
PC8. Solutions to Selected Problems
Problem PC1.1
a) A = ε c l = 60 L mol-1 cm-1 x 0.01 mol L-1 x 1 cm = 0.60 = 60 %
b) A = ε c l = 3,000 L mol-1 cm-1 x 3.5 x 10-5 mol L-1 x 1 cm = 0.105 = 10.5 %
c) A = ε c l = 1.4 L mol-1 cm-1 x 0.25 mol L-1 x 0.5 cm = 0.175 = 17.5 %
d) A = ε c l = 23,000 L mol-1 cm-1 x 2.5 x 10-6 mol L-1 x 1 cm = 0.0575 = 5.75 %
e) A = ε c l = 14,000 L mol-1 cm-1 x 0.015 mmol L-1 x 1 cm = 14,000 L mol-1 cm-1 x 0.015 x 10-3 mol L-1 x 1 cm = 0.21 = 21 %
Problem PC1.2.
a) ε = A /c l = 0.30 / (0.01 mol L-1 x 1 cm) = 30 L mol-1 cm-1
b) ε = A /c l = 0.25 / (0.025 mol L-1 x 1 cm) = 10 L mol-1 cm-1
c) ε = A /c l = 0.30 / (0.01 mol L-1 x 1 cm) = 543 L mol-1 cm-1
d) ε = A /c l = 0.66 / (0.025 m mol L-1 x 1 cm) = 0.66 / (0.025 x 10-3 mol L-1 x 1 cm) = 26,400 L mol-1 cm-1
Problem PC1.3.
a) blue
b) red
c) orange
d) violet
e) green
Problem PC1.4.
a) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/1 x 10-5 m = 1.98 x 10-20 J
b) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/125 x 10-9 m = 1.59 x 10-18 J
c) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/1025 x 10-9 m = 1.94 x 10-19 J
d) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/450 x 10-6 m = 4.42 x 10-22 J
e) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/850 x 10--10 m = 2.3 x 10-18 J
Problem PC1.5.
a) λ = hc/E = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/1.46 x 10--17 J = 1.36 x 10-8 m
b) λ = hc/E = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/4.72 x 10--24 J = 4.21 x 10-2 m
c) λ = hc/E = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/9.26 x 10--17 J = 2.15 x 10-19 m
Problem PC1.6.
a) E = hν = hc/λ ; so ν = c/λ; or λ = c/ν = 3.0 x 108 m s-1/6.7 x 1010 s-1 = 4.48 x 10-3 m
b) λ = c/ν = 3.0 x 108 m s-1/1500 x 106 s-1 = 0.2 m
c) ν = c/λ = 3.0 x 108 m s-1/9.8 x 10-10 m = 3.06 x 1015 s-1
d) ν = c/λ = 3.0 x 108 m s-1/4.3 x 10-12 m = 7.0 x 1019 s-1
Problem PC1.7.
a) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (1 mm x 10-3 m mm-1) = 1.99 x 10-22 J
That's for one molecule. On a per mole basis, E = 1.99 x 10-22 J x 6.02 x 1023 mol-1 = 120 J mol-1 = 0.12 kJ mol-1.
b) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (1000 nm x 10-9 m nm-1) = 1.99 x 10-19 J
That's for one molecule. On a per mole basis, E = 1.99 x 10-19 J x 6.02 x 1023 mol-1 = 120,000 J mol-1 = 120 kJ mol-1.
c) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (1 m) = 1.99 x 10-25 J
That's for one molecule. On a per mole basis, E = 1.99 x 10-25 J x 6.02 x 1023 mol-1 = 0.120 J mol-1 = 1.2 x 10-4 kJ mol-1.
d) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (500 nm x 10-9 m nm-1) = 3.98 x 10-19 J
That's for one molecule. On a per mole basis, E = 3.98 x 10-19 J x 6.02 x 1023 mol-1 = 239,000 J mol-1 = 239 kJ mol-1.
Problem PC1.8.
Blue.
Problem PC1.9.
Ultraviolet light, with a shorter wavelength than visible light, is much higher in energy and potentially more damaging.
Problem PC2.3.
a) d → d
b) π → π*
c) MLCT
Problem PC2.4.
a)
b) The one on the left can relax by channelling some energy into molecular vibration, especially its cis-trans isomerisation. The one on the right can't do that because its rotation is restricted by the presence of the ring.
c) Of course! It's crawling with pi bonds. A strong pi-pi* transition in the visible region seems likely.
d) Probably not. It does not have restricted rotation, so the cis-trans isomerisation route is available for relaxation.
e) A = ε b c, so ε = A / b c = 0.77 / (1 cm x 10-6 M) = 7.7 x 105 M-1 cm-1
f) That's a large molar absorptivity constant. It's allowed.
g) Undoubtedly this is that pi-pi* transition we were thinking about earlier.
h) If the compound binds to zinc, it probably does so via bidentate coordination. The resulting ring restricts the degrees of freedom in the compound so it can't undergo cis-trans isomerisation, closing off a route to rapid relaxation.
i) A compound like this could be used to detect metal ions such as Zn2+. Because the amount of fluorescence depends strongly on the Zn2+ concentration, it could be used to measure the amount of the ion present.
Problem PC2.5.
a)
b) An orange complex would absorb blue light, its complementary colour.
c) A blue laser would work. Maybe somewhere around 476 nm.
d) Notice a Re(II) site results, because it has transferred an electron to the ligand.
e)
f) The reduction potentials (1.4 V > 0.3 V) suggest transfer from copper (I) to rhenium (II).
g) i) The carbonyl stretches would be observed somewhere around 2000 cm-1.
iii) The electron transfer from the Cu(I) to the Re(II) site would result in a Re(I) site. The carbonyl stretch would shift to a lower wavenumber. That is because the lower oxidation state on the metal results in increased backbonding to the π-accepting carbonyls.
iii) At that distance, an outer sphere mechanism seems likely; it isn't clear how something could bridge that distance, other than the peptide chain itself, which probably lacks sufficient conjugation to conduct electrons.
h) Tryptophan acts as a stepping stone between copper and rhenium. Phenylalanine, with a higher reduction potential than rhenium, does not.
i)
Problem PC3.1.
a) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (180 nm x 10-9 m nm-1) = 1.10 x 10-18 J
That's for one molecule. On a per mole basis, E = 1.10 x 10-18 J x 6.02 x 1023 mol-1 = 665,000 J mol-1 = 665 kJ mol-1.
For comparison, the relatively strong and unreactive C-H bond in methane has a bond dissociation energy of only 440 kJ mol-1. (That's a thermodynamic value; to actually break the bond would cost more input of energy, to get over the kinetic energy barrier for bond cleavage.)
b) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (476 nm x 10-9 m nm-1) = 4.17 x 10-19 J
That's for one molecule. On a per mole basis, E = 4.42 x 10-19 J x 6.02 x 1023 mol-1 = 251,000 J mol-1 = 251 kJ mol-1.
c) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (645 nm x 10-9 m nm-1) = 3.08 x 10-19 J
That's for one molecule. On a per mole basis, E = 3.08 x 10-19 J x 6.02 x 1023 mol-1 = 138,000 J mol-1 = 138 kJ mol-1.
Problem PC3.2.
a) λ = 1 / wavenumber = 1 / 3105 cm-1 = 3.22 x 10-4 cm x 0.01 m cm-1 = 3.22 x 10-6 m
E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (3.22 x 10-6 m) = 6.17 x 10-20 J
That's for one molecule. On a per mole basis, E = 6.17 x 10-20 J x 6.02 x 1023 mol-1 = 37,000 J mol-1 = 37 kJ mol-1.
b) λ = 1 / wavenumber = 1 / 1695 cm-1 = 5.90 x 10-4 cm x 0.01 m cm-1 = 5.90 x 10-6 m
E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (3.22 x 10-6 m) = 3.37 x 10-20 J
That's for one molecule. On a per mole basis, E = 3.37 x 10-20 J x 6.02 x 1023 mol-1 = 20,000 J mol-1 = 20 kJ mol-1.
c) λ = 1 / wavenumber = 1 / 963 cm-1 = 1.04 x 10-3 cm x 0.01 m cm-1 = 1.04 x 10-5 m
E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (1.04 x 10-5 m) = 1.91 x 10-20 J
That's for one molecule. On a per mole basis, E = 1.91 x 10-20 J x 6.02 x 1023 mol-1 = 11,500 J mol-1 = 11.5 kJ mol-1.
Problem PC3.3.
a)
b) Ru(bpy)32+ would be a terrible reducing agent. The reduction potential of Ru(bpy)33+ is very high. That means Ru(bpy)32+ would not give up an electron very easily.
c) ΔG = - n F E0
ΔG = - 1 x 97,485 J V-1 mol-1 x 1.26 V = -123, 000 J mol-1 = -123 kJ mol-1
d) It absorbs in the blue part of the spectrum and appears orange.
e) It absorbs very strongly, so probably not d-d. It is probably MLCT, from the ruthenium to the π* in the bpy ligand.
f) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (450 nm x 10-9 m nm-1) = 4.42 x 10-19 J
That's for one molecule. On a per mole basis, E = 4.42 x 10-19 J x 6.02 x 1023 mol-1 = 266,000 J mol-1 = 266 kJ mol-1.
g) Ru2+ would be low spin d6, a singlet ground state. The excited state will also be a singlet state.
h) 615 nm is in the orange region of the spectrum. This is light given off by the complex as it relaxes, so it is the colour we see.
i) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (615 nm x 10-9 m nm-1) = 3.23 x 10-19 J
That's for one molecule. On a per mole basis, E = 3.23 x 10-19 J x 6.02 x 1023 mol-1 = 195,000 J mol-1 = 195 kJ mol-1.
j) Stokes shift = 615 nm - 450 nm = 165 nm
k) ΔE = E1 - E2 = 266 - 195 kJ mol-1 = 71 kJ mol-1
However, it would not be lost all at once, but in small increments equivalent to the differences between vibrational states.
l) If we were to reduce Ru(bpy)33+ directly into an excited state, we would arrive at a state much higher in energy than the ground state. That reduction would be harder to accomplish. In this case, the ending state would be 195 kJ mol-1 higher than Ru(bpy)32+.
ΔG = 195 - 123 kJ mol-1 = 72 kJ mol-1
E0 = - ΔG / n F = - (72 kJ mol-1 x 1000 kJ J-1) / (1 x 96,485 J V-1 mol-1) = -0.75 V
m) The oxidation of Ru(bpy)32+* would be very favourable compared to the oxidation of Ru(bpy)32+. The former is a much better reducing agent.
Problem PC5.1.
The longer the wavelength, the lower the energy. Photons of wavelength longer than 240 nm would not have enough energy to overcome the barrier for the dioxygen-cleaving reaction.
Problem PC5.2.
According to the Planck-Einstein relation:
E = hν
or, since ν = c / λ
E = hc / λ
in which h = Planck's constant = 6.625 x 10-34 Js,
c = speed of light = 3.0 x 108 m/s,
ν = frequency,
λ = wavelength.
a) E = hc / λ
E = (6.525 x 10-34 Js)(3.0 x 108 m/s) / (220 nm)(10-9 m/nm)
E = 9.03 x 10-19 J
b) E = hc / λ
E = (6.525 x 10-34 Js)(3.0 x 108 m/s) / (325 nm)(10-9 m/nm)
E = 6.12 x 10-19 J
Problem PC5.3.
Remember, the mole is the conversion unit from the molecular scale to the macroscopic scale.
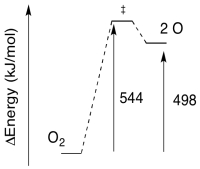
a) E = (8.28 x 10-19 J / photon)(6.02 x 1023 photons/mol)
E = 543,770 J/mol
E = 544 kJ/mol
b)

Problem PC5.4.
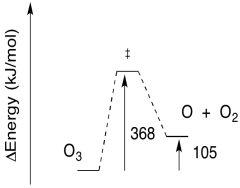
a) E = (6.12 x 10-19 J / photon)(6.02 x 1023 photons/mol)
E = 368,146 J/mol
E = 368 kJ/mol
b)
Problem PC5.5.
The reactions must take the same pathway, and go over the same barrier, forward and back.
a) The reverse barrier: E = 544 - 498 kJ/mol
E = 46 kJ/mol
b) The reverse barrier: E = 368 - 105 kJ/mol
E = 263 kJ/mol
Problem PC6.1.
a) The original PDI has an absorption maximum at just under 500 nm. It absorbs blue-green, so it would be expected to appear red-orange.
b) The longest wavelength absorbed is approximately 625 nm.
c) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/625 x 10-9 m = 3.18 x 10-19 J
That's the energy of a photon. A mole of photons would have energy multiplied by Avogadro's number, NA.
E = 3.18 x 10-19 J x NA = 3.18 x 10-19 x 6.02 x 1023 mol-1 = 1.91 x 105 J mol-1 = 191 kJ mol-1
d) If we approximate E = ΔG, and given that ΔG = - nFE0
Then for this single-electron excitation, E0 = - ΔG / n F = - 1.91 x 105 J mol-1 / (1 x 96,485 J V-1 mol-1) = -1.97 V
e)
f) Given the structure of PDI, the transition is probably π --> π*.
g) The longest wavelength absorbed shifts toward the red, to about 700 nm, after dipping in acid. The energy of the transition is lowered to
E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/700 x 10-9 m = 2.84 x 10-19 J
E = 2.84 x 10-19 J x NA = 3.18 x 10-19 x 6.02 x 1023 mol-1 = 1.71 x 105 J mol-1 = 171 kJ mol-1
h) These very flat molecules can probably stack very tightly together. The distance between the π electrons on one molecule and the π* orbital on a neighbouring molecule is very small. An intermolecular transition is possible.
i) What happens when the film is dipped in acid? It gets protonated. The anionic phosphate groups would become neutralized. The molecules would be able to stack even more closely together, lowering the energy required to excite an electron from one molecule to the other.
j) The onset of the reduction wave appears to be about -0.40 V, as shown by the peak in the cyclic voltamogram.
k)
l)
m) E0(vs Ag+/AgCl) = E0(vs NHE) + 0.20 V (i.e. the positive reduction potential of Ag+ vs. NHE indicates an electron is
i) E0(vs Ag+/AgCl) = - 0.10 V + 0.20 V = + 0.10 V
ii) E0(vs Ag+/AgCl) = + 1.23 V + 0.20 V = + 1.43 V
iii) E0(vs Ag+/AgCl) = + 0.83 V + 0.20 V = + 1.03 V
n) The excited state can be reduced by placing an electron in the hole vacated by the excited electron. This level is 1.97 V below the conductance band in energy, which has a reduction potential of -0.40 V (its potential is 1.97 V more positive than the conductance band).
Thus, -0.40 V + 1.97 V = + 1.57 V.
o)
p)
q) The phosphates probably coordinate to the cobalt oxide, forming a bridge for electron transfer.
Problem PC6.2.
a) Ag+(aq) + NO3-(aq) + Bu4N+(aq) + Br -(aq) → AgBr(s) + Bu4N+ (aq) + NO3- (aq)
b) They absorb in the violet-blue range and would appear yellow-orange.
c)
d) A nanometer is 10-9 m, whereas a picometer is 10-12 m. A picoparticle is 1,000 times smaller than a nanoparticle.
e)
f) They absorb across the visible spectrum and appear black.
g)
Problem PC7.1.
One simple reason may be the presence of additional nitrogen atoms in the ligand. These additional electronegative atoms may make the complex more electrophilic, or more able to accept additional electron density.
Problem PC7.2.
Problem PC7.3.
a)
b)
This site is written and maintained by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (with contributions from other authors as noted). It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry/span> by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
This material is based upon work supported by the National Science Foundation under Grant No. 1043566.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Navigation: