
04/02/2008
Moles, Molar Mass, and Avogadro's Number
To understand how substances react chemically, we need to be able to determine how many molecules of one substance reacts with another substance. In the lab we do not measure molecules directly but rather the mass of the reacting chemicals and products. Therefore we have to be able to convert between mass in grams and molecules.
Consider 4 different boxes, each containing different fruits (a raisin, grape, apple, and grapefruit). Let's assume all the boxes without fruit in them have the same mass. Now put fruit in them.

If each box contained the same number of pieces of fruit, then the box with the fruit with the heaviest piece of fruit would obviously weigh more. Conversely, if the mass of the boxes were the same, then the box with the lightest piece of fruit would have the most pieces of fruit. If you knew the weight of each piece of fruit, you could determine the number of pieces of fruit in the box.
Now consider atoms like He, C, or Ti, and a molecule like sulfuric acid, H2SO4. They are arranged in term of increasing atomic weight, or molecular weight - the sums of the atomic weight, for the molecule sulfuric acid. Hence if different boxes contained equal number of these different atoms or molecules, then the box with sulfuric acid would weight most, and the box with He would weigh least. Conversely, if the boxes weighed the same amount, the box containing the lightest atom, He, would contain more particles than the others.
Lets go back to the periodic table
|
Group |
||||||||||||||||||
| Period | 1A | 2A | 3B | 4B | 5B | 6B | 7B | 8B | 9B | 10B | 11B | 12B | 3A | 4A | 5A | 6A | 7A | 8A |
| 1 |
1 H 1.01 |
|
2 4.00 |
|||||||||||||||
| 2 |
3
Li |
4 Be 9.01 |
|
5 B 10.81 |
6 12.01 |
7 14.01 |
8 16.00 |
9 19.00 |
10 20.18 |
|||||||||
| 3 |
11 22.99 |
12 24.31 |
13 Al 26.98 |
14 Si 28.09 |
15 30.97 |
16 32.07 |
17 35.45 |
18 39.95 |
||||||||||
| 4 |
19 39.10 |
20 40.08 |
Sc |
Ti |
V |
Cr |
Mn |
Fe |
Co |
Ni |
Cu |
Zn |
Ga |
Ge |
As |
Se |
Br |
Kr |
| 5 | Rb | Sr | Y | Zr | Nb | Mo | Tc | Ru | Rh | Pd | Ag | Cd | In | Sn | Sb | Te | I | Xe |
| 6 | Cs | Ba | La | Hf | Ta | W | Re | Os | Ir | Pt | Au | Hg | Ti | Pb | Bi | Po | At | Rn |
| 7 | F | Ra | Ac | Rf | Db | Sg | Bh | Hs | Mt | Uun | Uuu | Uub | ||||||
|
Atomic # Symbol Avg. Atomic Mass |
Lets look at carbon. Its atomic number is 6 (meaning it has 6 protons and 6 electrons in the neutral atom). It has an average atomic mass of 12.01. What are the units? Grams? Pounds? Tons? Obviously not. Notice that H has an atomic mass of 1.01. Whatever the units are, that means that an atom of C has a 12 times the mass of an atom of H. The mass derives mostly from neutrons and protons, and we neglect the contribution from electrons. H has 1 proton and 0 neutrons, while C has 6 protons and 6 neutrons (in its most common form, although there are some rarer "isotopes" that have more neutrons ). The mass unit we use is the atomic mass unit (AMU). The H atom (with one proton) has a mass of 1 AMU. Carbon with 6 protons and 6 neutrons has mass of 12 AMU.
Now if we had two boxes with identical masses, one containing H atoms and one C atoms, we could say that there are more atoms in the H box than in the C box. Likewise if the box containing C atoms had 12 times the mass of the box containing the H atoms, we could say that they had an equal number of atoms in each box.
In our lab, we can't determine that mass of a few atoms of a substance. However, we can easily measure 1 g of H atoms and 12 g of C atoms (assuming that the atoms didn't chemically react with each other and were stable, which we know they aren't). In these two boxes, we would have the same number of atoms. How many? A very large number called Avogadro's Number which is 6.022 x 1023 atoms. We also define another term since that number is much to big to use routinely. We define an amount of an element which contains 6.022 x 1023 atoms of that element, or in the case of C and H, 12 and 1g, respectively, as one mole of that element.
The atomic weight of an atom of a pure element like Cu, Ti, etc, or the molecular weight of a molecule (calculated by adding up the atomic weights of all of its atoms), both expressed in grams, contains 6.022 x 1023 atoms or molecules of that substance. or one mole. The molar mass is the atomic (for atoms) or molecular weight (for molecules) expressed in grams. The "amount" of a substance that contains 6.022 x 1023 particles of that substance is 1 mole of that substance. You must be able to convert, using the factor-label method to convert between moles, molar mass, and number of molecules.
ANIMATION: Triangular Relationship of mass, molecules, and moles
It just so happens that 12.0 g of 12C (the form of C with 6 protons and 6 neutrons) has 6.022 X 1023 atoms. Too bad it is such a bizarre number. It would have been better if it were 1 billion, but there is nothing any of us can do about it. We define 1 mole of 12C as the mass of 12C that contains 6.022 X 1023 atoms., which , as described above, has a mass of 12.0 g. An atom of H has a mass 1/12 of carbon. (Look at the atomic weights) Therefore 6.022 X 1023 atoms of H would weight 1/12 of 12.0 g, or 1.0 g, which again happens to be the atomic weight of H expressed in grams. Likewise, H2O (molecular weight of 18.0) has a molar mass of 18.0 g. 18.0 g of water is 1 mole of water and contains 6.022 X 1023 molecules of water. Hemoglobin (MW = 64,000) has a molar mass of 64,000 g. 64,000 g of hemoglobin contains 6.022 X 1023 molecules of hemoglobin. By the way 1 mole of elephants would be 6.022 X 1023 elephants.
3/08: Easiest:
Na + Cl to NaCl
atoms, molecules, dozen, gross, mol, molar mass
amu 23, 35.5, 58.5
to
g: 23 g, 35.5 g to 58.5 g
1 mol + 1 mol to 1 mol
thenj
Na(s) + Cl2 give 2NaCl
Interpreting Chemical Equations
In class we wrote and balanced a chemical equation for the reaction of gold sulfide (Au with a 3+ charge) with hydrogen gas (H2). The balanced equation below illustrates the important features of the equations
Au2S3 + 3 H2 ------> 2 Au + 3 H2S
This chemical equation can be translated into English as follows:
1 molecule of gold sulfide reacts with 3 molecules of hydrogen to produce 2 atoms of gold plus 3 molecules of hydrogen sulfide.
Both sides of a chemical equation, like a mathematical equation, can be multiplied by the same number. The table below shows various amounts of reactants and products that are obtained by multiplying the chemical equation by some number.
multiply by |
Au2S3
|
3 H2
|
2 Au
|
3 H2S
|
- |
1 molecule | 3 molecules | 2 atoms | 3 molecules |
2 |
2 molecules | 6 molecules | 4 atoms | 6 molecules |
12 |
12 molecules | 36 molecules | 24 atoms | 36 molecules |
OR |
1 DOZEN | 3 DOZEN | 2 DOZEN | 3 DOZEN |
6.02 X 1023 |
1(6.02 X 1023) molecules |
3 (6.02 x 1023) molecules |
2(6.02 x 1023) atoms |
3(6.02 x 1023) molecules |
OR |
1 mole molecules. | 3 moles molecule | 2 moles atoms | 3 moles molecule |
| which equals | 490 g | 6.0 g | 394 g | 102 g |
Please note the following:
Stoichiometry
The coefficients in front of balanced chemical equations tell us the number of moles of reactants that react to form a specific number of moles of products. The reaction stoichiometry is the quantitative relations between the amount of reactants consumed and products formed in chemical reactions as depicted in the balanced chemical equations. Stoichimetric relationship can be used to determine that in the chemical reaction below :
Au2S3 + 3 H2 --> 2 Au + 3 H2S
490 g of Au2S3 reacts with 6 g H2 to give 394 g of Au and 192 g of H2S. (See table above). Simple proportions could be used to determine amounts of gold and hydrogen sulfide produced if the reactants were present at half the amounts listed above.
What would happen, however, if we had 490 g of gold sulfide and 100 g of hydrogen? Or a million g of hydrogen? Clearly not all the hydrogen could react. Hydrogen is in excess and some would be left after the reaction. Gold sulfide is the limiting reagent and the amount of products produced would be determined only by the amount of the gold sulfide, and not the hydrogen.
A simple example of the concept of excess/limiting reagents is illustrated in the model below. You have two different 2D structures, a triangle and a square with a triangular indentation the same size of the triangle. You have 1 square and 4 triangles.
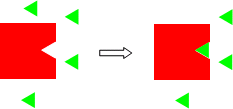
The triangular indentation is lined with Velcro, and the triangle with the opposite type of Velcro. Now mix them together. Since only one triangle can fit into the indentation in the square, after mixing one square-triangle "complex" results and 3 triangles are left over. For an obvious chemical example, burn a 10 g piece of coal that is pure carbon in the air. Obviously oxygen in the air is in huge excess and the coal is limiting.
Animation: combustion of a hydrocarbon (excess oxygen)
Animation: combustion of a hydrocarbon (limiting reagent)
Animation: stoichiometry
Quiz: Stoichiometry
Concentration
The concentration of a solution is the mass (in
grams) of a substance that is dissolved in a given volume (in cubic
centimeters or cm3) of solution. The substance that is
dissolved can be a solid (like salt), a liquid (like vinegar), or a
gas (like oxygen or carbon dioxide). Concentration can be found by
dividing the mass of the substance dissolved by the total volume of
solution. This can written in a formula:
concentration = mass of a dissolved substance/volume of
solution.
Expressing Solution Concentrations:
There are different ways to express concentration of a solute dissolved in a solvent. In each way, concentration is expressed as the amount of solute (g, ml,) dissolved in a given amount (g, ml) of SOLUTION. We will consider two different ways to determine concentration - % concentration and Molarity
% concentration ( v/v, or m/v): which can be any of the following
Molarity (M)
The later statement can be seen from the following conversion:
1 M = 1 mol/L = 1 mol/L X 1000 mmol/mol X 1L/1000 mL = 1 mmol/mL
Hence a 0.1 M NaCl solution has 0.1 mole NaCl/L solution or 0.1 mmol NaCl/ml solution. In an analogous fashion 10 g/L = 10 mg/ml
% concentration is used if your main interest is knowing how much solute is in a given amount solution. Molarity units are most often used when you wish to determine changes in the the amounts and concentrations of reactants and products in a chemical reaction that occurs in solution.