In lab 2 you will determine the mass of dissolved solids and all solids in a sample of water. It sounds simple, but there are some important features of measurements that you need to understand. Chapter 1 presents some information, and Appendix 2 has a review of significant figures. In this handout, we will explore important features of measurement. In this document, we will use a simple question, "What is the weight of a 1997 penny?" to to illustrate several points:. Lab workers must make measurement everyday. They might have an unknown chemical substance and would like to know what it is, so they devise tests to measure fundamental properties of the substance. They then can compare these measured properties to the properties of known substances to determine the nature of their unknown. Lessons learned from measuring the weight of water apply to many circumstances.
PROBLEM: MEASURE THE AVERAGE WEIGHT OF PENNY
Ways to determine the weight (mass) of an object.
There are many ways to measure the weight of a penny. There are many questions that are raised by the simple question. Did I mean what is the most accurate weight of a single penny, or did I mean what is the average weight of 1997 pennies in general? Each penny must have a slightly different weight. The simpler problem is to determine the weight of a single penny. You could simply weigh it one time and take that as the weight. A better way might be measure the weight of the same penny 5 times, and average them, since you would probably get a different weight each time, depending on you measuring device and how you read it. A more complicated problem is to determine the average weight of 1997 pennies. The complexity increases since you would get slightly different weights for the same penny each time you weighed it, and each different penny would also have a slightly different weight to start with. If I am asking about the average weight of a 1997 penny, you could take 5-1997 pennies and measure the weight of each one, add the weights, and then divide by 5. Alternatively, you could determine the weight of all 5 together, and divide by 5. Which method is better? We will investigate this problem later. It probably is intuitive that the more pennies you measure and/or the more times you weigh a given penny, the more accurate your average weight would be.
Imagine that you measure the weight of a single penny a thousand times on each of two different analytical balances. You will get a distribution of measured values for the penny for each of the balances used. Balance 1 reads to 0.005 grams but balance 2 reads to 0.05 grams. You have been told that the mass of the penny, determined on an ultra sensitive balance, is 5.015000005 g. What is the best value for the weight of the penny? What kind of error might be associated with your best value? The kind of distribution of values you would get for a typical measurement is shown in the graph below. The middle value in the distribution, the one most likely recorded most often, represents the best value for the measurement. The measured values farthest away on the x axis are those least likely to be recorded.
DISTRIBUTION OF MEASUREMENTS
Accuracy and Precision
Before we can discuss how good your measured values are, we need to discuss two common terms - accuracy and precision. The following example will help you explore the different between these two concepts. You are throwing darts at a dart board. You can throw them with great precision, but little accuracy. In this case all the darts would be clustered together on the board, but unfortunately not at the bullseye. In contrast, you can throw with great accuracy and precision if the darts are all clustered at the bullseye.
How accurate is your measurement? How should you report it?
In they penny example above, you used two balances which differ in their sensitivity. Let us assume that your measuring devise is accurate (properly calibrated so the average weight of the pennies is centered on the "actual average".) It is important to know the limits on the measuring ability of the instrument. A simple example illustrates these points. A friend of yours, who dropped chemistry after the first lab, thought he could accurately determine the mass of objects just by holding them in his hand. To test his abilities, you blindfolded him, gave him a 5.00 g mass (to calibrate his arm), and then had him hold a new mass of 10.0 g. In his blunt and arrogant fashion, he calmly announced that the mass was 7.2345430783 g.
What was wrong with his determined mass? First, his number was not accurate. He was low at least 2.7 g from the actual mass of the object in his determination. Second, he reported the result to such a degree of sensitivity, that one would have thought he was a bionic man with a built in modern electronic microbalance, not just a simple lever and pulley system of bones, muscles, tendons, and ligaments. He reported his mass to 10 decimal places. We can assume from his measurement that he could measure mass to an accuracy of + 0.0000000001 g. What he really implied by his measurement was that the actual mass was between 7.2345430782 and 7.2345430784 g. He measured (in his mind) with absolute certainty the numbers 7.234543078 (10 figures) and the last one (the 10th decimal place) he estimated with some uncertainty. He actually then measured 11 figures, and each figure contains significant information concerning the mass of the object. Each of these figures in significant. He has reported his answer to 11 significant figures. A bit too many sig. fig.'s don't you think?
There is a place and time for such profound accuracy, sensitivity, and such a large number of significant figures. For example, consider Dirac's number, which describes the magnetic properties of a spinning electron. Recent experimental measurements put this number at 1.00115965221 + 0.00000000004. Not bad, given that the theoretical value for this number, derived from the modern theory of quantum electrodynamics, is 1.00115965246 + 0.00000000020! The measured value is probably incredibly accurate, as reflected by the large number of significant figures, the small associated certainty, and the closeness to the theoretical value. Richard Feyman suggests that is equivalent to measuring the distance between New York and Los Angeles to within the distance of a human hair. Some rules for determining the number of significant figures are:
What use are significant figures. It became clear when you realized that some properties can not be measured directly on a fancy instrument, but rather must be calculated from a series of other measurements (for example the average of many measurement, the density of water, calculated from mass and volume. It is here where significant figures come in handy in allowing us to determine the uncertainty of a calculated result. Another example pops to mind to clarify this use of significant figures. In the lab you had to make a solution of sodium chloride (NaCl) containing 30.80 g NaCl in water so that the final volume of the solution was 5.27 X 102 ml. You needed to measure mass of NaCl, the volume of the solution, and from that to calculate the concentration of the solution in g/ml.
So what is the concentration in g/ml of the NaCl solution? Is it 0.058, 0.0584, 0.05844, or 0.058444 g/ml? This is not a trivial question. For calculated results use the following rules:
![]()
WebCT Quiz: Select Measurement as the Quiz
You now have an idea of what will be required of your measurements. You must measure some property of the pennies with an instrument of sufficient sensitivity to measure small differences in the property of interest. In addition, you must know the limits of accuracy of your instruments, so that you can report your measured property to the right number of decimal places and significant figures. For those properties which are calculated from a series of measurements, the final result must have the correct number of significant figures. You should try to achieve the most accurate measurements and results possible, with the maximum number of significant figures allowable, based on the measuring instruments available to you.
Reading the best value for a measurement.
It is important to know how to read an instrument. Some instruments such as electronic balances show the measure value digitally. Just read the value from the digital readout but remember that the last digit is uncertain with a tolerance of x + some number. If the values has to be read between lines, such on an analog scale, you can usually divide the distance between the two lines into tenths and estimate the best value to that level of certainty. The last estimated number has some significance so it is still a significant digit. The example below shows a special case that will help you determine if 0's in a number are significant.
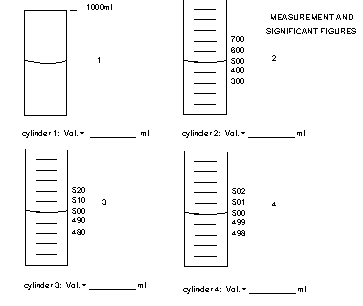
All the flasks read 500 mL, but how many sig. fig's should you use? Scientific notation works best. The best values are
| Cylinder 1 | 5 x 102 | 1 Sig Fig |
| Cylinder 2 | 5.0 x 102 | 2 Sig Fig |
| Cylinder 3 | 5.00 x 102 | 3 Sig Fig |
| Cylinder 4 | 5.000 x 102 | 4 Sig Fig |
Errors in your measurements/calculation: absolute, relative error, and standard deviation.
All measurements have errors associated with them. Hence all calculated results must have an error associated with it, which can be determined by taking into account the errors associated with the individual measurement. There are many ways to estimate the error associated with a calculated , as in the examples below.
Relative error and range of possible values: : (Example: measuring the average weight of 5 pennies, either by measuring them individually and calculating the mean, or weigh them all together, and calculate the mean.) How much error is associated with this calculated result? The easiest way to quantitate it is to use the relative error. Assume that the absolute error in each measurement is + 0.001 g. Imagine in a worst case scenario that each of the five measurements was 0.001 g to high. The other worse case scenario would be that each of the measurements was 0.001 g to low. (In reality, some of the measurement would be 0.001 too high, and some too low.) That implies that if each pennies were measured individually, the sum of the measured masses for 5 pennies would be x + 0.005 g. The average mass per penny would be 1/5 of that result, or x/5 + 0.001 g. If the five penny were weighed together, the weight would be y + 0.001 g, so the average mass per penny would be 1/5 of that result, or y/5 + 0.0002 g.
Standard Deviation as a measure of error: (Ex: Measuring the weight of a single penny) In this example, we obtained a distribution of measured values. We can obtain the best value for the weight by determining the mean of the measurement. One way to calculate the error is to determine the standard deviation (S.D) of the measurements, using statistics. Clearly the S.D. obtained using the more sensitive balance is less than the with the less sensitive balance. To calculate the S.D., first calculate the mean, X. Then take each X value you measured and subtract from it the mean, X. This gives the deviation from the mean of each measurement: Xi-X. If your measured value is greater (>) than X, then Xi-X > 0. If the measured value is less than (<) the mean, Xi-X < 0 or negative. You expect some deviations to be positive and some to be negative. Next square all the deviations for each measurement., (Xi-X)2. All these numbers are now positive. Next add all the squared deviations for all the measurements and divide by n-1 where n is the number of measurements.
Σ(Xi - X)2/n-1 which gives the approximate average of the deviations squared. (If you divided by n instead of n-1 it would be the average of the deviations squared). Now take the square root of this number and you get the standard deviation for the measurement. Remember our normal distribution curve in the beginning. It should follow that if we measured one penny 1000 times on balance that reads to 0.005 grams, the S.D. for those measurements will be less than one the reads to a value of 0.05 g.