Almost all the chemistry that we will study this year deals with reactions of molecules in aqueous solution. This also applies to reactions in the body, which consists of greater than 60% by weight of water. Before we study solutions, we need to review our definition of a solution. In our first unit on matter, we defined solutions as homogeneous mixtures - In homogenous mixtures, the particles are so small that they never separate on standing or in simple centrifugation, and do not interfer with light passing through the mixture. Hence the mixture appears clear. The solution can not be separated into its component parts by filtration. It can be separated by other physical techniques like chromatography (as in lab 1), distillation, etc. If we sample a given solution at different locations, it will have the same composition at every location.
The material that dissolves in a liquid is called the solute. The liquid that dissolves the solute is called the solvent. Of course we can have solution of solids (like salt), liquids (like ethanol) and gases (like carbon dioxide) - all solutes - dissolved in the liquid solvent. Likewise the air is a soluton of gas solutes in a gas solvent. Some substance can dissolve in water, others can't. Substances that can't dissolve in water often dissolve in other solvents. Some solid substances dissolve in a solvent like water to different extents. When no more solute can be added to a solvent, we say the solution is saturated with the solute. Any additional solid added will remain as a solid in the solution.
ANIMATION: Saturation of water with NaCl
![]() SICD 14-2 Saturated,
Unsaturated Solutions
SICD 14-2 Saturated,
Unsaturated Solutions
A liquid solute may not dissolve in water. In this case, it will form a discrete layer either above or below the water layer (depending on its density). Such a liquid is immiscible in the solvent. Some liquid solvents dissolve in any proportion in water. Such a liquid solute is completely miscible.
ANIMATION: Saturation of water (blue) with a liquid (yellow)
Solubilty of molecules in water and hexane
A knowledge of IMF's can help us understand the solubility of different substances (solutes) in different liquids (solvents). In class I did a series of demostrations which showed if different solutes were soluble in two different solvents, water and hexane, whose structures are shown below.
A quick inspection of these solvents show them to be quite different. hexane, a clear, colorless liquid at room temperature, is completely nonpolar and interacts with other hexane molecules through London forces. In contrast, water, a clear, colorless liquid at room temperature, is polar and interacts with other water molecules through H-bonds. You might expect they might dissolve different types of solutes. Explore the solubility differences of the different solutes below in hexane and water. Develop a law that will allow you to predict the solubility of a substance in water or hexane, and then develop an hypothesis that helps explain the law.
1. NaCl - sodium chloride:

NaCl is a salt held together by ionic bonds. In a sense it is as polar a substance as you can get. It dissolves in water (as you know from experience) but not in hexane.
2. I2 - Iodine:
![]()
Iodine, a covalent solid, in contrast to water, is completely nonpolar. It dissolves in hexane to produce a purple-colored solution. It didn't dissolve in water.
TENTATIVE LAW: From the above two examples, we can surmise that polar molecules dissolve in polar liquids, and non-polar molecules in nonpolar liquids.

Acetic acid was soluble in water and insoluble in hexane. An inspection of the molecule shows that is is predominately polar with a small nonpolar CH3 group. Our tentative law seems to work so far!

Oleic acid, found in olive oil, is soluble in hexane but not soluble in water. It formed a separate layers in water. In this example, most of the molecule is nonpolar (the long C-H tail) with just a small part at the right end being polar. The nonpolar sections wins out and determines its solubility in water.
MODIFIED TENTATIVE LAW: From the above examples, we can surmise that molecules dissolve in polar liquids if the solute is predominately polar, or in nonpolar solvents if the solute is predominately nonpolar.
![]()
Methanol, a clear, coloress liquid, dissolved in water but only slightly dissolved in hexane. Again this molecule is predominately polar so our modified law is supported. Please note that methanol dissolves but does not form ions in solution.
![]()
![]()
Octanol, a mostly nonpolar molecule, dissolves in hexane but formed a separate layer in water. Again our modified law is upheld.
We can use our tentative law to predict whether the following substances are soluble in water or hexane.
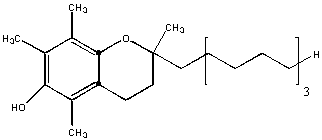
This molecule is almost entirely nonpolar. Hence it will be insoluble in water and soluble in hexane. The is an example of a fat-soluble vitamin. One early definition of fat is biological molecules that are soluble in organic solvents like hexane.
![]()

In vitamin C, every C is attached to an oxygen atoms. This molecule is polar and will dissolve in water, but not hexane.
![]()
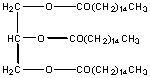
This molecule is also a fat and is the predominant type of fat stored in fat tissue in your body. There are 9 polar carbons, but 42 non polar C's. It is insoluble in water and soluble in hexane. Triglycerides are the major type of substance in vegetable oils.
![]()
We arrive at the following conclusions:
REMEMBER, JUST BECAUSE A SOLUTE DISSOLVES IN WATER DOESN'T IMPLY THAT IT DISSOCIATES INTO IONS LIKE SOLUBLE SALTS AND STRONG ACIDS!
Image: How methanol, CH3OH dissolves in water.
You should now be able to predict the solubity of different substances in water and other solvents. Take for instance O2. Would you expect this to be very soluble in water? It's not since it is nonpolar and can't form ion-ion, H-bonds, or dipole-dipole interactions with water. We can't get by by "breathing water" since not enough O2 can be dissolved in water. That's why we have a protein in our blood called hemoglobin which specifically binds and carries O2, effectively increasing the "dissolved" concentration of oxygen by 100 fold. Given this info, how can you explain the photo below:
Micelles and Bilayers
We have seen that the solubility properties of molecules strongly depend on how much of the molecule is polar and how much is nonpolar. Consider stearic acid, shown below, which has 18 carbons. The end containing the two oxygens (shown in red) is polar, but the rest of the molecule is completely nonpolar (shown in blue). We can draw a "cartoon" model of this model as a circle - representing the polar end or "head group" with a single connecting line - representing the long.nonpolar "tail".
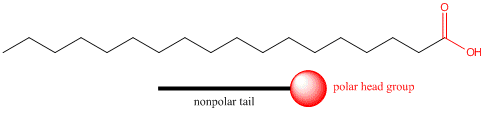
Pretend you are that molecule with your head representing the polar head group and the rest of your body the nonpolar tail. Now dive into water. How would you orient yourself in water? There are several possible ways. A small number of these molecules might be soluble in water (remember even insoluble salts dissociate to a small degree to form a few ions). Mostly the nonpolar tail wants to get out of the water, while the polar head like to stay in the water. There are two ways this can be done. Some of the molecules migrate to the surface of the water, with the nonpolar tails sticking out into air, away from water, to form a monolayer on the top of the water. Others will self-aggregate, through IMF's to form a spherical structure in which the nonpolar tails are sequested from water and the polar head are facing the water. This structure is called a micelle. Detergents consist of molecules with very similar structure to stearic acid pictured above. They form micelles in water. Grease from clothes or foods, normally not soluble in water, can "dive" into the middle of the micelle and be carried off by this structure. Notice that there is not water inside the micelle as you can see by selecting Micelles below.
![]() SICD 14-11 Surfactants
(Micelles)
SICD 14-11 Surfactants
(Micelles)
Now consider another molecule somewhat similar to stearic acid, called a phoshpolipid. A typical phospholipid structure is shown below. Notice it has a polar end (shown in red), but in contrast to stearic acid above, it has two long nonpolar tails shown in blue. We can draw a "cartoon" model of this as a circle - representing the polar end or "head group" with two connecting lines - representing the two long nonpolar "tails".
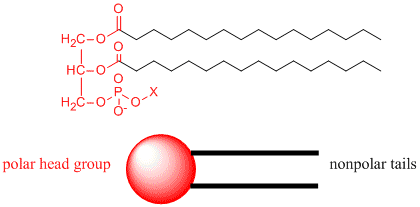
How would you orient this molecule in water? There are several possible ways. A small number of these molecules might be soluble in water as above. Mostly, however, the nonpolar tails wants to get out of the water, while the polar head like to stay in the water. Again, some of the molecules migrate to the surface of the water, with the nonpolar tails sticking out into air, away from water, to form a monolayer on the top of the water. Others will self- aggregate, through IMF's to form a bilayer or membrane. Because there are two tails per head group, the tails can't pack together as tightly. Imagine the bilayer or membrane curving around and eventually meeting. A structure like this would look like a small biological cell. In contrast in a micelle, the interior of this little cell, or liposome, is filled with water which can interact through IMF's to the head groups of the inner leaflet of this membrane. The head groups of the outer leaflet of the membrane interact through IMF's with the bulk water.
Phospholipids are the basic component of actually biological membranes. Liposomes are useful since they are simple models of actual biological membranes. In addition, they are starting to be used therapeutically. Toxic drugs, like those used in chemotherapy, can be incorporated into the aqueous volume inside a liposome where they can be targeted to specific tumor cells.
Liposomes and micelles seem to be complicated structures. However their formation and existence can be predicted from the simple solubility properties of these molecules and the concepts of IMF's.
Colloids: Add
![]() SICD 14-10
Colloids
SICD 14-10
Colloids
CONCENTRATION
The concentration of a solution is the mass (in
grams) of a substance that is dissolved in a given volume (in cubic
centimeters or cm3) of solution. The substance that is
dissolved can be a solid (like salt), a liquid (like vingegar), or a
gas (like oxygen or carbon dioxide). Concentration can be found by
dividing the mass of the subtance dissolved by the total volume of
solution. This can written in a formula:
concentration = mass of a dissolved substance/volume of
solution.
The units of concentration are then grams/cubic centimeter or grams/cm3. People use concentration when they are talking about solutions. In a way it is analogous to another concept with which students have trouble - density.
DENSITY: What is density. It has to do with both the mass of an object and the volume of an object, just like concentration has to do with the mass of a dissolved sustance and the volume of the solution.
DENSITY IS LIKE CONCENTRATION:
Peole use density when they want to determine the total mass of an object in a certain volume of that object. The object can be anything: a solid, a liquid, a gas, a mixture, a solution. The density of an object equals its mass divided by its volume. It has units of grams/cm3 .
density = mass of an object /volume of the object. Consider for a moment a cube with each side being 1 cm.
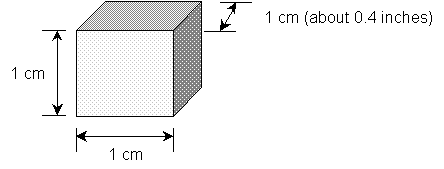
Now it's easy to measure the mass of this
object. Place the object on a scale or balance. The volume of the
cube can be calculated by the simple formula.
Volume = V = length X width X height = 1 cm X 1 cm X 1 cm
1 cubic centimer = 1 cm3.
It's also easy to calculate the volume of an object if it is a simplegeometric shape. If it has a more complicated shape, you can measure its volume indirectly by putting it into a container with water. Look at the picture below.
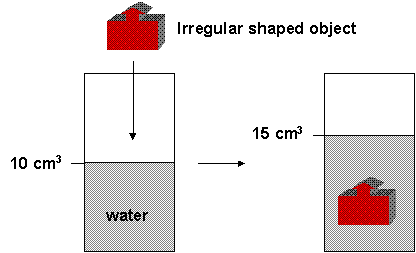
What is the volume of the object? The total volume in the container with the object is equal to the volume of the water plus the volume of the solid. Hopefully you can tell that the volume of the object is 5 cm3. For this to work, the object can not dissolve. You can calculate the volume by putting an insoluble solid into water and determining the volume change of the water.
Now you have the mass of the object and its volume so you can calculate the density. Again, the units of density is grams/cubic centimeter.
EXAMPLE OF DENSITIES: What is the density of a cubic centimeter of a substance? Check out the chart below which shows the density of various subtances.
|
SUBSTANCE |
PHYSICAL STATE |
DENSITY (g/cm3) |
|
hydrogen |
gas |
0.000090 |
|
oxygen |
gas |
0.00143 |
|
stryfoam |
solid |
about 0.08 |
|
alcohol |
liquid |
0.785 |
|
water |
liquid |
0.998 |
|
salt |
solid |
2.16 |
|
aluminum |
solid |
2.70 |
|
copper |
solid |
8.96 |
|
lead |
solid |
11.34 |
|
gold |
solid |
19.32. |
Now for some really strange numbers. People
have estimated the density of outer space, with its stars, planet,
comets, and mostly "empty" space. The average density of space is
about 3 x 10-24 or
0.000000000000000000000003 g/cm3 which should tell you
that it really is mostly empty. Now at the opposite end, there are
some incredibly dense stars called neutron stars. The stars have an
unbelievably high density of about 1 x 1015 or
1,000,000,000,000,000 g/cm3.. To get the same density you
would have to compress a cube of water with sides of 0.6 miles into a
cube 1 cm on each side!
You can increase the volume of a substance by compressing it into a smaller volume. If you had a room full of feathers that might have a mass of 1000 grams, and you squash them into a smaller shape, what changes? The total mass doesn't but the volume get smaller. Since density is equal to mass divided by the volume, the density gets bigger. The picture below shows how decreasing the volume of an object increases its density.

The same diagram could represent a solution. You can increase the concentration of a solution by evaporating the water (but not the dissolved substance). The mass of the dissolved substances remains the same, but the volume it dissolves in decreases. Therefore, its concentration goes up. Hopefully you can see the similarities and differences between concentration of a solution and the density of a substance!
ANIMATION: Solution of Increasing Concentration
Expressing Solution Concentrations:
There are different ways to express concentration of a solute dissolved in a solvent. In each way, concentration is expressed as the amount of solute (g, ml,)dissolved in a given amount (g, ml) of SOLUTION. We will consider two different ways to determine concentration - % concentration and molarity
% concentration (w/w, v/v, or w/v): which can be any of the following
Molarity (M)
The later statement can be seen from the following conversion:
1 M = 1 mol/L = 1 mol/L X 1000 mmol/mol X 1L/1000 mL = 1 mmol/mL
Hence a 0.1 M NaCl solution has 0.1 mole NaCl/L solution or 0.1 mmol NaCl/ml solution. In an analogous fashion 10 g/L = 10 mg/ml
% concentration is used if your main interest is knowing how much solute is in a given amount solution. Molarity units are most often used when you wish to determine changes in the the amounts and concentrations of reactants and products in a chemical reaction that occurs in solution.
To make a solution of a given % concentration or molarity, a given amount of solute is added quantitatively (using a balance to measure mass or a volumetric pipet to measure volume) to a solvent, the solute dissolved, and then transfered quantitatively to a volumetric flask. Solvent is added to a given final volume of total solution. Solutions can then be diluted to make less concentrated solutions. Dilutions of 1 --> 10 (10 fold dilution), 1 --> 100 (one hundred fold dilution) or 1 --> 1000 (thousand fold dilution) are often conveniently made. To make a 1000 fold dilution, you can take 1 mL of the stock solution, add it quantitativley to a 1 L volulmetric and add solvent to a volume of 1 L.
Since most reactions that we will deal with in this class occur in solution, we need a easy way to determine the amount or reactants used and products consumed. Consider the following two reactions:
In both of these reactions 1 mole of each reactant reacts to form 1 mole of each product. When dealing with aqueuous solutions, we usually know the molarity of the solution and the volume of each reactant solution. The above equations dont say the 1 ml of each reactant or 1 g of each reactant forms 1 ml or 1 g of each product. Rather it states that number of moles of reactants and products. Unit analysis shows that for any given reactant or product:
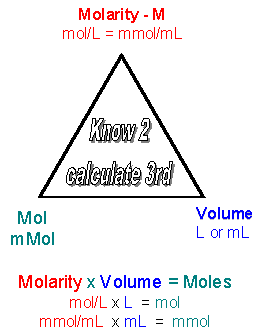
Molarity x Volume = M x Vol = Mol/L x L = moles. Or using easier units:
Molarity x Volume = M x Vol = mMol/mL x mL = mmoles
Given two of the following qualities (M, V, moles) you should be able to detemine the other quantitiy, since M = mol/V. Likewise you should be able to convert from M = mol/L = mmol/ml to g/L = mg/ml.
In equation 2 above, 1 mole of HCl reacts with 1 mole of NaOH to form 1 mole of NaCl and 1 mole of H2O. If you are given a volume and molarity of a given solutions, you must convert these units to moles, since the chemical equations describes the number of moles. Then you can determine the number of moles of product, which can be converted to a volume or molarity. Given 2 of the following quantities, you can get the other: Molarity, moles, volume.
Practice solution concentrations, dilution, and stoichiometry calculations in the quiz below.