| Table 1: Wave functions and their components | ||||
| n |
|
m |
|
orbital shapes |
| 1 | 0 | 0 |
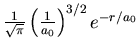 |
 1s 1s |
| 2 | 0 | 0 |
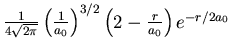 |
 2s 2s |
| 2 | 1 | 0 |
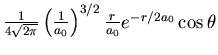 |
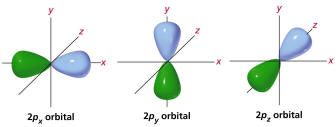 |
| 2 | 1 |
|
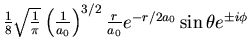 | |
| 3 | 0 | 0 |
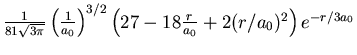 |
 3s 3s |
| 3 | 1 | 0 |
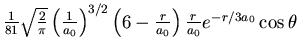 |
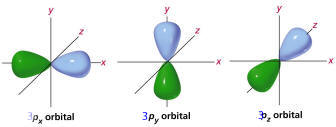 |
| 3 | 1 |
|
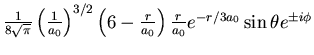 | |
| 3 | 2 | 0 |
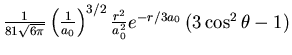 |
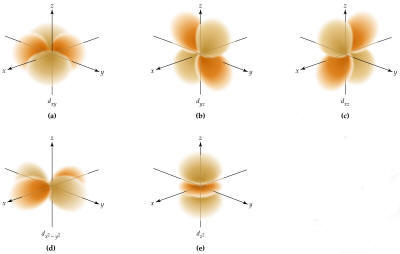 |
| 3 | 2 |
|
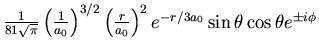 | |
| 3 | 2 |
|
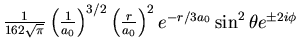 | |
http://panda.unm.edu/courses/finley/P262/Hydrogen/WaveFcns.html
| Table 1: Wave functions and their components | ||||
| n |
|
m |
|
orbital shapes |
| 1 | 0 | 0 |
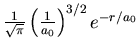 |
 1s 1s |
| 2 | 0 | 0 |
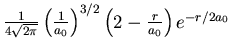 |
 2s 2s |
| 2 | 1 | 0 |
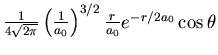 |
 |
| 2 | 1 |
|
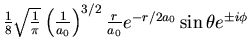 | |
| 3 | 0 | 0 |
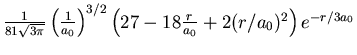 |
 3s 3s |
| 3 | 1 | 0 |
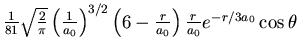 |
 |
| 3 | 1 |
|
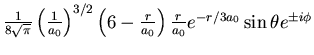 | |
| 3 | 2 | 0 |
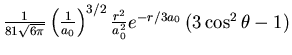 |
 |
| 3 | 2 |
|
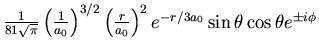 | |
| 3 | 2 |
|
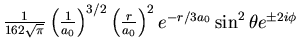 | |