Dalton - Atomic Theory. The atom is indivisible. Atoms of different elements differ in properties, including mass. Atoms combine to form compounds
Account for Laws of
- mass conservation
- combining volumes
- constant composition/multiple prop.
Could not account for arrangement of elements in the periodic table; for the periodicity of chemical and physical properties of elements
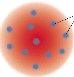
Electron (negative charge) interspersed in sea of protons like plums or raisins in pudding
Accounted for existence of protons and neutrons in atom
Same as for Dalton model
Rutherford:
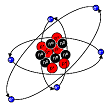
Nuclear, (Planetary) Model. Small dense nucleus with all protons and neutrons. A necessary consequence is that the electron must be orbiting the nucleus like a planet, otherwise it would be pulled into the nucleus. The attractive force for the electron and proton is the Coulombic force (F = kQ1Q2/r2)
Accounts for scattering of alpha particles (He nucleic) from gold sheet, which led to concept that nucleus exists. Electrons closer to the nucleus would have lower energy, those farther away higher energy. Rational basis for absorption spectra of atoms (light energy promote electrons to higher energy levels) and emission spectra (release of light energy as electron falls to a lower energy level).
Same as Dalton model but more.
Couldn't account for the stability of the atoms. The orbiting electron (with its attached EM field) is effectively an oscillating charge. It would produce a EM wave - a wave in the field. Hence the electron should lose energy and spiral into the nucleus. This is all based on classic physics. Also couldn't account for emission spectra of elements, which show discrete lines indicating the only certain energies of electrons in the H atom are permitted. Theory wouldn't predict that only certain orbits were allowed. (An empirical equation, Balmer/Rydberg equations, predicted the wavelengths of the emitted light, which were related to integers.)
Light had been shown earlier by Maxwell to be an electromagnetic wave. Waves can constructively/destructively interfere with each other. Light can be shown through two slits (or even one as I demonstrated in class) to produce an interference pattern. However, the photoelectic effect, explained by Einstein, showed that light acted as a particle. DeBroglie showed that nanoparticles like electrons can behave as waves. Electrons give an interference pattern as illustrated by an example showing the interference pattern when electrons pass through two two slits . The wavelengths of macroscopic objects are too small for detection, but this is not true for nanoscopic objects.
Bohr: First Quantized Model of the hydrogen atom.
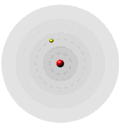
His model used a classical description of motion of the electron in H and of the electrostatic forces between the proton and electron. Knowing the importance of integers form the Balmer/Rydberg equation, he assumed (without justification) that the angular momentum, Pang, was quantized (could have only discrete values), where Pang = mvr = nh/2π. Using this assumption, he deduced that for the H electron, the energy (E), its velocity (v) and its radius from the nucleus (r) were quantized.
By assuming that angular momentum was quantized, he created the stable atom. He theory gave exact predictions for the emission spectra of the hydrogen atom.
There was no real justification for his assumption that the Pang was quantized. His theory worked only for the H atom, and couldn't predict the emission spectra of other atoms. His theory was really a hybrid of a classical physics and the new emerging quantum mechanical understanding of the world.
Still doesn't account for chemical and physical properties of atoms and arrangment of elements into the periodic table.

The first model of the atom that contained elements of the wave properties of the electron. Assumed a circular orbit for the electron. If the electron in this orbit acted as a wave, for it to remain stable, and not exhibit destructive interference, it must create a standing wave around the nucleus. (An interactive demonstration of a standing wave.) The conditions for a standing wave to be stable is that the circumference of the orbit must equal an integral number of wavelengths of the electron, or :
2πr
= nλ.
OR 2πr
= nh/p = nh/mv
mvr = Pang = nh/2π.
Based in part on the wave-like nature of the electron. By assuming this property, which was experimentally verified through diffraction experiments, he was able to deduce, not assume, that the angular momentum, Pang, of the H electron was quantized.
Same as the original Bohr model. This model was still a hybrid of classical and the new quantum mechanics.
Schrodinger Wave Mechanical Model: This is the first totally quantum theory (nonclassical) of the H atom, based on the wave properties of the electron. The properties of the electron are specified by wave functions ψwhich are solutions of the Schrodinger Equation: Hψ = Eψ . The solutions give atomic orbitals defined by quantum numbers n, l, ml, and ms. The wave function ψ can not be directly detected. It can by indirectly detected since ψ2 give the probability of detecting an electron (Born). Orbitals are regions of space around the nucleus where the electron has a high probability of being located. The electron has specific properties (mass, charge, and spin), but other properties are dynamics and contextual - they depend both on the electron and the measuring device. such properties often are paired (such as momentum and position). Diffraction patterns from electrons passing through slits of increasingly small size show that as the position of the electron is known to higher certainty, the uncetainty in momentum (sidewise) increases, as elaborated in the Heisenberg Uncertainty Principle: ΔxΔp > h/4π.
Theoretically predicts the experimentally observed properties of the H atom. It can be modified to deal with polyatomic atoms by stating that the specified electron is attracted to a nucleus whose charge is effectively reduced by shielding by all other electrons, reducing the multielectron atom to a one electron atom experiencing a Zeff nuclear charge.
The theory clearly accounts for the chemical and physical properties of atoms and the arrangement of elements into the periodic table. No other theory about the atoms has such predictive power.
Works explicitly for atoms or ions with only one electron.