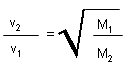The following is a list of equations which you should know
(have memorized) and
be able to explain/manipulate. The equations with yellow highlight are for
second semester Gen. Chem.
| Equation |
Meaning |
F = ma
 |
Force = mass x acceleration (m/s/s or m/s2).
If a net force is acting on a particle, it will accelerate. If the net
force on a particle is zero, the particle will not accelerate. Rather
it will stay at the same velocity. If it were initially at rest, it will
stay at rest. |
Fgrav = km1m2/r2
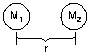 |
Gravitational force - force of attraction acting
between 2 bodies separated by distance r between their centers and of mass m1
and m2 - is inversely proportional to r2 |
Felectro = kQ1Q2/r2
 |
Electrostatic force (Couloumb's Law) - force of attraction
or repulsion acting between 2 charged bodies separated by distance r between
their centers and of charge Q1 and Q2 - is
inversely proportional to r2. |
E = -F(r ); Eelect = -kQ1Q2/r
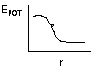 |
Force = -ΔE/ΔR
(or -ΔE/Δx) so
ΔE = -FΔx
or F = - slope (minus sign since F goes in opposite direction of
increasing potential. |
Epot = mgh
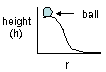 |
Potential energy = mass x acceleration due to gravity (9.8
m./s2) x height |
Ekin = �
mv2
 |
Kinetic energy = �
x mass x velocity2 |
p = mv
 |
Momentum of particle (p) = mass x velocity
Would you rather be hit by a mosquito or an elephant, each with a
velocity of 1 m/s? |
W = -Fext
Δx
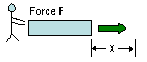 |
Work (units of energy) =
- force X distance moved
(Fext = friction, the opposing force), work done on rectangle |
c = λυ
 |
speed of light (c) = wavelength (λ)
x frequency (υ)
m/s
m x 1/s |
E = hυ = hc/λ
 |
Energy of a photon = Planck constant (h) x frequency
(υ) = h x speed of light(c) divided by wavelength (λ) |
p = h/λ
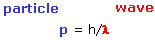 |
momentum of particle = Planck constant (h) /wavelength
(picture of DeBroglie) |
ΔpΔx
>
h/4π =hbar/2
 |
Heisenberg Uncertainty Principle: uncertainty in momentum x
uncertainty in position is greater than or equal to Planck constant/4
π. |
q = mcΔT
 |
heat change (J) = mass m x specific heat (J/(goC)
x tej change in temperature |
| ΔH =
Σ(nΔHbond
enthalpy react. - Σ(nΔHBH
prod) |
change in enthalpy for a written reaction = sum
of n x the bond enthalpy of the reactants (energy required to break a bond)
- sum of n x the bond enthalpy of the reactants |
| ΔHo =
Σ(nΔHoform
prod) - Σ(nΔHoform
react) |
standard enthalpy for a written reaction = the
sum of n x the standard enthalpy of formation of the products - the sum of n
x the standard enthalpy of formation of the reactants (n values are the
stoichiometry coefficients from the balanced equation) standard enthalpy
of formation (kJ) = enthalpy change for the formation of one
mole of a substances from the pure elements in the standard state |
|
|
First Law of Thermodynamics: the change in
internal energy E of a system is equal to the heat transferred to or from
the system plus work done on or by the system. |
ΔE sys = E 2 - E 1
= q + w = q -P extΔV
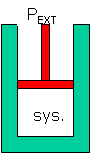
|
First Law of Thermodynamics if only PV work
(expansion/contraction of gas) : |
ΔEtot =
ΔEsys + ΔEsurr
= 0 = ΔEuniv
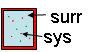 |
First Law of Thermodynamics for system and
surrounding (= universe) |
| ΔEsys = E2
- E1 = qv -PextΔV = qv |
Change in internal energy at constant V where qv
is heat transferred at constant V |
| ΔEsys = E2
- E1 = qp -PextΔV |
Change in internal energy at constant P when
only PV work |
|
ΔHsys = qp
+ PextΔV; Hsys = qp
+ PV
constant P and V, ΔHsys = qp

|
enthalpy and change in enthalpy for a system at
constant P |
|
PV=nRT Ideal Gas Law |
Ideal gas law where P is pressure, V is volume,
n is number of moles, T is temperature in K, and R is the ideal gas
constants. Use the correct units (dimensional analysis)
8.315 J/(K . mol)
= 0.08206 L
. Mol/
K .mol)
Note: all gases at the same P, V, and T have same number of
moles, n. |
|
E avg kin/mol = (3/2)RT |
Gives the meaning of T. |
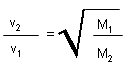 |
at given T, gas with higher molar mass has a
lower velocity. |
|
|
|
DStot
=
DSsys
+
DSsurr
> 0 or
DStot
=
DSsys
-
DHsys/T
> 0
|
Second Law of Thermodynamics, for a spontaneous process |
|
DGsys =
DHsys -
TDSsys
= - TDStot
|
|
|
DSo sys =
SnS0prod
-
SnSoreact
|
|
| ΔGo =
Σ(nΔGoform
prod) - Σ(nΔGoform
react) |
|
| Keq = (C)c(D)d]/[(A)a(B)b] |
for reaction: aA
+ bB
↔
cC
+ dD,
Keq is the equilibrium constant for the reaction where (A), (B),
etc are the equilibrium concentrations of reactant A, ...., and a, b, ....
are the stoichiometric coefficients in the balanced equation |
DGrx=DG0rx
+
RT ln {[(C)c(D)d]/[(A)a(B)b]
= DG0rx
+
RT ln Q
|
for reaction: aA
+ bB
↔
cC
+ dD
where (A), (B), etc are the actual concentrations of reactant A, etc at
a given time and Q is the reaction quotient
|
|
DG0rx
= -
RT ln Keq = -2.303RTlogKeq DG0rx
= DGrx
when all reactants/products in std state |
Relationship btw DG0rx
and Keq |
| Ka = [H3O+][A-]/[HA] |
For the reaction of an acid (HA)and water to
form the hydronium ion and the conjugate base of the acid (A-):
HA(aq) + H2O(l) ↔ H3O+
+ A-
Ka is the acid dissociation constant = equilibrium
constant assuming water is a constant. |
| pH = - log [H3O+];
pKa = - log Ka |
[H3O+] high, pH low; Ka
high, pKa low |
| pH = pKa + log [A-]/[HA]
Henderson-Hasselbach equation |
Ka = [H3O+][A-]/[HA]
log Ka = log [H3O+]
+ log [A-] - log [HA]
-log Ka = -log [H3O+]
- log [A-] + log [HA]
pKa = pH - log [A-]/[HA]
pH = pKa + log [A-]/[HA]
Gives pH as function of pKa, and
concentrations of weak acid and its conjugate base; Useful in buffer
calculations |
|
Keq = (C)c(D)d]/[(A)a(B)b]
Ka
= [H3O+][A-]/[HA]
a. Kw
= [H3O+][OH-] = 10-14
b. Kb =
[OH-][BH+]/[B]
KaKb = Kw
= 10-14
c. Ksp =
[cation]m[anion]n
|
Lots of equilibrium type expressions for the
following reactions:
a. H20 (l) + H20
(l) ↔ H3O+(aq) + OH-(aq)
- for autoionization of water
b. B (base) + H2O(l) ↔ OH-
(aq) + BH+(aq) - for reaction of a base
in water.
c. salt (s) ↔ m [cation] + n
[anion] where m and n are stoichiometric coefficients. |
|
C = i t |
C = charge in Coulombs = current i (amps, A = 1 C/s) x time (seconds)
Note: 1.60218 x 10-19 C/e- or 96,465 C/mol = 1
Faraday |
|
Eocell = Eocathode - Eoanode
= Eocathode
+ (- Eoanode )
 |
The standard reduction potential of a cell (consisting of two half cells) is
the standard reduction potential of the reaction that occurs at the cathode
(reduction) + the negative of the standard reduction potential of the
reaction that occurs at the anode (oxidation). The negative sign is
required since the standard reduction potential at the anode (where
oxidation occurs) is written for the reaction as a reduction, not an
oxidation. Eocell is +, then rx proceeds as written;
if - then rx proceeds in opposite direction. |
|
welect = qV welect = nFE |
electrical work available (J) = charge q (C) x Voltage (V or J/C)
electrical work available (J) = number of mol e- in each
1/2 rx times the Farady constant (C/mol) times the cell potential
(J/C) . This will give the welect available for the
stoichiometric number of mol of reactants. Ex:
Zn(s) + HgO(s) → ZnO(s) + Hg(l) for Hg cell, n =2 but welect
calculated will be per 1 mol of Zn(s) |
|
welect (J/mol reactant) = nFE = -ΔGrx
nFEo = -ΔG0rx
OR = ΔG0rx =
-nFEo |
ΔG0rx = -nFEo
gives relationship btw Eo and ΔG0rx.
If Eo + (when oxidation at anode produces e which flow to cathode
in spontaneous process, ΔG0rx.
< 0 |
|
ΔGrx = DG0rx
+
RT ln Q -nFE = -nFEo + RT lnQ or
E = Eo - (RT/nF) ln Q OR
E = Eo - (2.303RT/nF) log Q or E = Eo
- (0.0591/n) log Q (at 25oC) |
E = Eo - (RT/nF) lnQ is Nernst Equation gives
relationship between standard cell potential (under standard state
condition), and the actual cell potential under nonstandard state
concentrations of reactants and products. |
|
Eo = (2.303RT/nF) log Keq or log Keq = nFEo/2.303RT or nEo/0.0591 (25oC) |
At Equilbrium ΔGrx =0, E
=0, |
|
v = k[A] = - ΔA/ΔT = +
ΔP/ΔT |
For 1st order reaction A → P, k is 1st
order rate constant, units s-1 |
|
A = Aoe-kt k = 0.693/t
� |
For 1st order reaction A → P, Ao
is the initial [A] t � is the half
life of the reaction (time for half reactants to react) |
|
v = k[A]2 |
For 2nd order rx: A + A →
P, k is 2nd order rate constant, units M-1s-1 |
|
v = - kf[A] + kr[P] At equilibrium vf = vr
or Keq = [P]eq/[A]eq = kf/kr |
For reversible rx: A ↔ P, where kf
is the 1st order forward rate constant, kr is the 2nd order
reverse rate constant |
|
v = k [A]x[B]y |
For the general reaction aA + bB →
cC + dD,
where x and y are the stoichimetric
coefficients for the particular step in a reaction mechanism |
v = - (1/a) ΔA/ΔT = -
(1/b) ΔB/ΔT = (1/c)
ΔC/ΔT =
(1/d) ΔD/ΔT |
For the general reaction aA + bB →
cC + dD, |








![]()