Determination of Mechanism in Chemistry
Mathematical Tools in Kinetics
MK17. Solutions
Problem MK9.1.

Problem MK9.2.
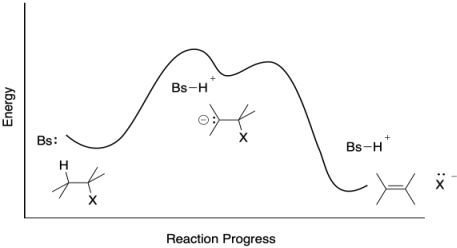
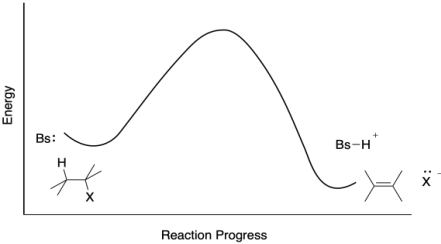
Problem MK9.3.

Problem MK.9.4
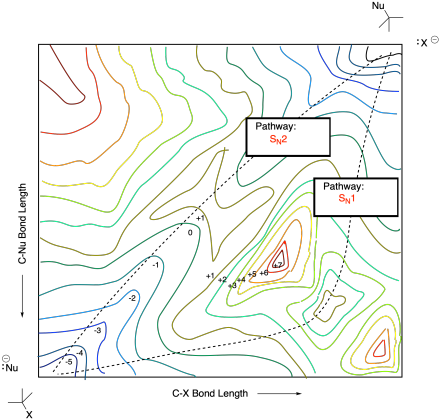
Problem MK.9.5
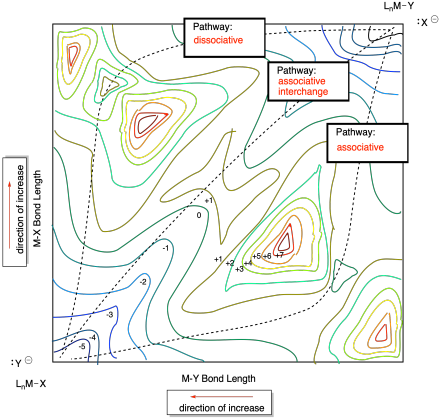
Problem MK10.1.
a) ΔG = -RTlnK = -(1.987 cal K-1mol-1)(273.15 + 35 K) ln(0.93)
= -(1.987)(308.15)(-0.0726)
= 44.4 cal mol-1 or 0.0444 kcal mol-1 (or 0.186 kJ mol-1)
b) ΔG = -RTlnK = -(1.987 cal K-1mol-1)(273.15 + 50 K) ln(7.6)
= -(1.987)(323.15)(2.028)
= -1,302 cal mol-1 or 1.30 kcal mol-1 (or 5.45 kJ mol-1)
c) ΔG = -RTlnK = -(1.987 cal K-1mol-1)(273.15 + 70 K) ln(3.8)
= -(1.987)(343.15)(1.335)
= -910 cal mol-1 or -0.910 kcal mol-1 (or 3.81 kJ mol-1)
Problem MK10.2.
a) ΔG‡ = RT{ln(kBT/h) - lnk}
= (1.987)(273.15 + 45 K){ln[(1.38 x 10-23 J K-1)(273.15 + 45 K)/(6.626 x 10-34 J.s-1)] - ln[3.7 x 10-5 s-1]}
= (1.987)(318.15){ln[6.626 x 1012] + 10.2046}
= (632.16)(29.552 + 10.2046)
= 25,132 cal mol-1 = 25.1 kcal mol-1 = 105 kJ mol-1
b) ΔG‡ = RT{ln(kBT/h) - lnk}
= (1.987)(273.15 + 65 K){ln[(1.38 x 10-23 J K-1)(273.15 + 65 K)/(6.626 x 10-34 J.s-1)] - ln[1.9 x 10-6 s-1]}
= (1.987)(338.15){ln[7.0427 x 1012] + 13.1737}
= (671.904)(29.583 + 13.1737)
= 28,7282 cal mol-1 = 28.7 kcal mol-1 = 120 kJ mol-1
c) ΔG‡ = RT{ln(kBT/h) - lnk}
= (1.987)(273.15 + 85 K){ln[(1.38 x 10-23 J K-1)(273.15 + 85 K)/(6.626 x 10-34 J.s-1)] - ln[ 4.8 x 10-7 s-1]}
= (1.987)(358.15){ln[7.459 x 1012] + 14.5495}
= (711.644)(29.6405 + 14.5495)
= 31,448 cal mol-1 = 31.5 kcal mol-1 = 132 kJ mol-1
Problem MK10.3.
a)

b)
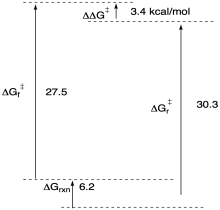
c)
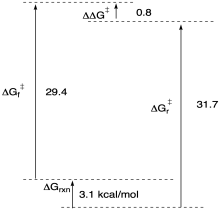
Problem MK11.1.
a)
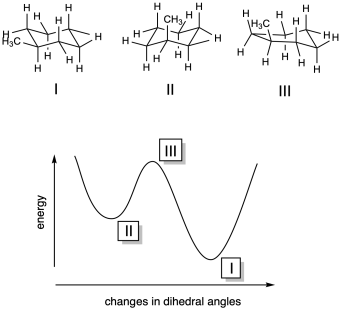
b) I is a global minimum; II is a local minimum; III is a maximum.
Problem MK11.2.
a)
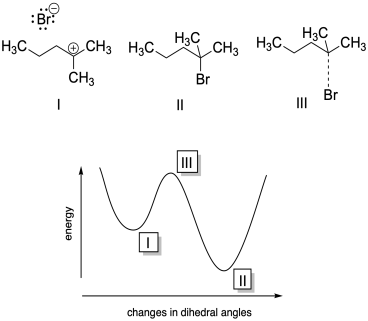
b) I is a local minimum; II is a global minimum; III is a maximum.
Problem MK11.3.
a)
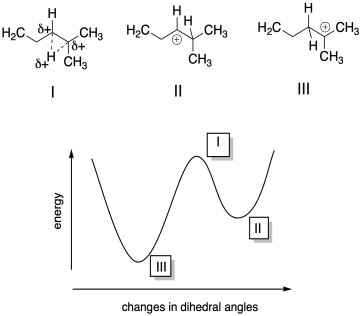
b) I is a maximum; II is a local minimum; III is a global minimum.
Problem MK12.1.
BDE = 2.86 cal/cm-1(19,898 - 7,598 cm-1) = 35.178 kcal/mol.
Problem MK12.2.
In both cases, a resonance-stabilized radical leads to easier bond cleavage, hence a weaker bond strength.
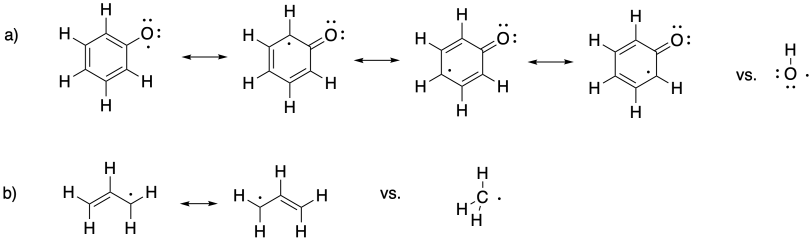
Problem MK12.3.
a) ΔG = - nFΔE = -(1)(96,485 J/V)(1 cal/4.184J)(1 kcal/1,000 cal)ΔE = -23.06 kcal/V
ΔG = - RTlnK = - 2.303RTlogK = 2.303RTpKa = (2.303)(1.987 cal/K mol)(298 K) pKa = 1.36 pKa kcal/mol
b) BDE (kcal/mol) = 1.37pKa + 23.06Eoox(PhO-) - 23.06Eored(H+) + 46 kcal/mol
= (1.37)(18) + (23.06)(0.55) + (23.06)(-0.4) +46 kcal/mol
= 24.66 + 12.68 - 9.22 + 46 kcal/mol = 74.12 kcal/mol
Problem MK13.1.
Approximating with whole number values for atomic mass:
a) a 12C-1H bond
μ = m1m2 / (m1 + m2)
= 12 x 1 / (12 + 1)
= 12 / 13
= 0.923
vs. a 12C-2H bond
μ = 12 x 2 / (12 + 2)
= 24 / 14
= 1.71
b) a 12C-1H bond
μ = 12 x 1 / (12 + 1)
= 0.923
vs. a 13C-1H bond
μ = 13 x 1 / (13 + 1)
= 13 / 14
= 0.929
c) a 35Cl-35Cl bond
μ = 35 x 35 / (35 + 35)
= 1,225 / 70
= 17.5
vs. a 35Cl-37Cl bond
μ = 35 x 37 / (35 + 37)
= 1,295 / 72
= 18.0
Problem MK13.2.
The value of μ almost doubles for a C-D vs. a C-H bond. In cases of heavier atoms, the change in reduced mass is only a small percentage. That leads to a very small isotope effect when heavier atoms are concerned.
Problem MK13.3.
This is a primary isotope effect in which a Pt-H or Pt-D bond is being broken. The relatively low value results from the non-linear geometry, since the methyl and hydride are cis- to each other on the platinum.

Problem MK14.1.
The phenolate anion delocalizes negative charge into the aromatic ring, whereas the benzoate anion does not. Thus, π effects show up more strongly in σ- than in σ.

Problem MK14.2.
The platinum is changing from Pt(II) to Pt(0). The more electron-donating the phosphine is, the more it stabilizes the higher oxidation state of the platinum, retarding the reductive elimination reaction.
Problem MK15.1.
a) approximate slope = -0.012 M / 25 s = -4.8 x 10-4 mol L-1 s-1
b) approximate slope = -0.002 M / 50 s = -4 x 10-5 mol L-1 s-1
Note that these slopes correspond to reaction rates.
Problem MK15.2.
a) dy/dx = -6e-3x b) dy/dx = 3e5x
Problem MK15.3.
a) dy/dx = 3 - 4x b) y = 0.9 - 10x + 24x2
This site was written by Chris P. Schaller, Ph.D., retired, College of Saint Benedict / Saint John's University (with contributions from other authors as noted). It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry
by Chris Schaller
is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Support for this project was provided by the Opens Textbooks Pilot Program of the U.S. Department of Education through a collaboration with the Libre Texts project at University of California, Davis.
Navigation:
Back to Determination of Mechanism
Back to Structure & Reactivity