Determination of Mechanism in Chemistry
MK14. Linear Free Energy Relationships
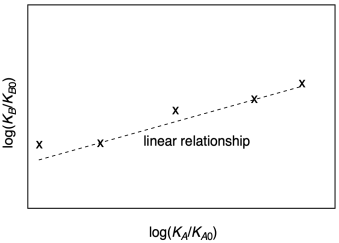
A linear free energy relationship is a quantitative correlation between two different reactions. To construct such a relationship, we measure either the rate constant or the equilibrium constant for the two different reactions using the same variables in each case. We plot the results from one reaction against the results from the other, using a logarithmic scale. If the plot is linear, we say that we have a linear free energy relationship between the two reactions. That linear correlation indicates that the factors governing one reaction (essentially the variables we chose to study) also govern the other.

Figure MK14.1. A linear free energy relationship.
The Hammett equation is one of the most widely used examples of a linear free energy relationship. It is based on the ionization of benzoic acid and its derivatives. The influence of different substituent groups on the acidity of benzoic acid is well understood. If you take two benzoic acid derivatives, p-XC6H4CO2H and p-C6H4CO2H, most college-level chemistry students will be able to make an argument about which one is more acidic, based on their general knowledge of the electronic properties of X and Y. If X is a nitro group, NO2, but Y is a methoxy group, CH3O, then it's reasonable to expect the nitro derivative to be more acidic than the methoxy derivative. That's what we see when we compare the pKa values: p-nitrobenzoic acid has a lower pKa than benzoic acid, meaning the proton is more tightly held in the former. p-Methoxybenzoic acid has a higher pKa than benzoic acid, indicating the methoxy derivative is less acidic.
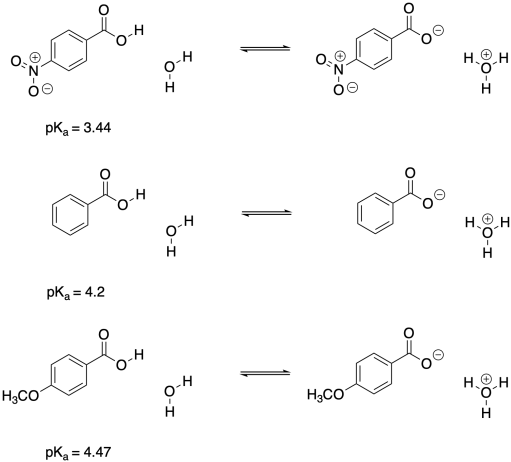
Figure MK14.2. Benzoic acid derivatives and their pKa values.
That's because the nitro group is much more electron-withdrawing, whereas the methoxy is overall electron-donating by virtue of the oxygen lone pairs. The nitro group is both sigma-withdrawing, because of the electronegative nitrogen and oxygen atoms, and pi-withdrawing, because of the double bond to the more electronegative oxygen. Although the oxygen in the methoxy group makes it a sigma-withdrawing group, the lone pair allows for pi-donation, and pi-donation in this case (from oxygen to carbon) is the dominant effect.
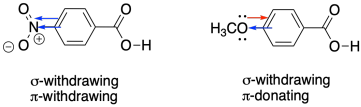
Figure MK14.3. σ and π effects may reinforce or conflict with each other.
The result is that nitrobenzoic acid is more acidic because of the relatively large amount of positive charge placed on the proton compared to regular benzoic acid, not to mention the stabilizationof the deprotonated benzoate anion by the electron withdrawing group. Methyoxybenzoic acid is less acidic because it is more electron-rich.
Well, we have pKa data for a lot of different benzoic acid derivatives. We have them for different X groups such as nitro and methoxy and we have them for X groups in different positions (ortho-, meta-, or para). That data indicates a very straightforward dependence of pKa on the electronic effects of the substituent group, whether X is electron donating or electron withdrawing. That set of data gives us a baseline with which we can compare other reactions so that we can see whether the electron demands of a particular reaction work the same way.
Louis Hammett was a mid-twentieth century professor at Columbia University who first compiled this information in an effort to study the electronic parameters of different reactions.1 He chose benzoic acid, C6H5CO2H, the parent compound in this series, as the standard to which he could compare the other derivatives. He compared these values by taking the ratio of the equilibrium constant of XC6H4CO2H to that of C6H5CO2H. A compound more acidic than benzoic acid would result in a value greater than one, whereas a compound less acidic than benzoic acid would result in a fraction. In short, the more acidic the compound, the larger the value. Hammett then chose to take the log of this value, resulting in a parameter that he called σ (sigma).
σ = log [Ka(XC6H4CO2H) / Ka(C6H5CO2H)]
Taking the log renders values of σ that are positive for compounds more acidic than benzoic acid and negative for compounds less acidic than benzoic acid. Why take that extra step? It's a pretty common practice in chemistry, physics or engineering. If you are trying to determine the relationship between two things, you will plot one against another. Maybe they seem to vary together -- as one gets bigger, so does the other -- but not in a linear way. It frequently happens that two parameters in nature are instead related exponentially, by a "power law". In that case, taking the log (or graphing on log paper instead of regular graph paper) will provide a straight line.
So, if we have another reaction, and we have a possible mechanism that seems like it would be subject to electronic considerations similar to those that govern acidity, we could compare data from this other reaction to these σ values from the benzoic acid series. A linear relationship would indicate a similar electron demand in the two reactions.
We could plot either equilibrium constants or rate constants against σ, but suppose in this case we plot rate constants. The Hammett Equation states:
log [k/k0] = ρ σ
In other words, there is a linear relationship with a proportionality constant called ρ (rho). The larger the rho value, the more strongly the reaction depends on the electron withdrawing or donating effects. In the Hammett equation, k0 refers to the rate constant for the parent, non-substituted compound; it's a reference point, just as in the definition of σ.
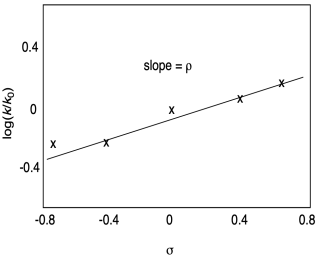
Figure MK14.4. An example of a Hammett plot.
To make this idea more concrete, here's an example. Hammett measured rates of reaction of about a dozen different benzoyl chloride derivatives with methanol. In this reaction, we think about the benzoyl chloride as an electrophile and the methanol as a nucleophile. We might expect this case to track with benzoic acid acidity because the reaction would be promoted by electron withdrawing groups and hampered by electron donating groups on the benzene.

Figure MK14.5. Methanolysis of benzoyl chloride and related derivatives.
If we plot the Hammett equation (producing a graph that's often called a Hammett plot), we do get a straight line, with a rho value of 1.47. It's a positive slope, meaning the reaction depends in the same way on electronic factors as the acidity of benzoic acid.
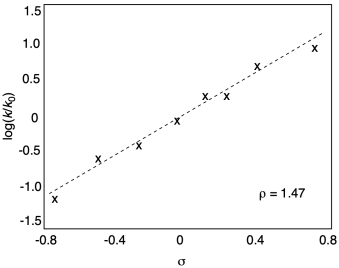
Figure MK14.6. Hammett plot for methanolysis of benzoyl chloride and related derivatives.
Here is a table that shows a range of examples of σ values. You can see how groups that we think of as electron withdrawing in electrophilic aromatic substitution, for example, have positive values of σ. These substituents result in increased acidity compared to benzoic acid. There are other groups that we think of as electron withdrawing in electrophilic aromatic substitution, and these substituents have negative values of σ. These substituents result in decreased acidity compared to benzoic acid.
Table MK14.1. σ values of different substituents.
| Group | σ |
| NH2 | -0.66 |
| OCH3 | -0.27 |
| CH3 | -0.17 |
| F | 0.06 |
| Br | 0.23 |
| CO2R | 0.45 |
| CF3 | 0.54 |
| CN | 0.66 |
| NO2 | 0.78 |
Let's take a completely different reaction, in which we expect the benzene derivative to act as a nucleophile. Hammett looked at a series of anilines and their reaction with plain benzoyl chloride. In this case, the aniline should act as a nucleophile.

Figure MK14.7. Aminolysis of benzoyl chlorides.
When we plot the rate data, we get a negative slope. This reaction depends on electronics in a way opposite to benzoic acid acidity. The more electron-rich the system, the better the nucleophile, and the faster the reaction.
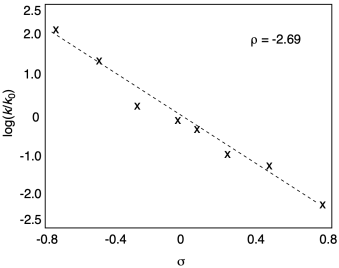
Figure MK14.8. Hammett plot for aminolysis of benzoyl chlorides.
Do things always work out this way? Not necessarily. We could have a reaction that doesn't clearly depend on these electronic factors, and so we would observe no correlation. We might get something like this.
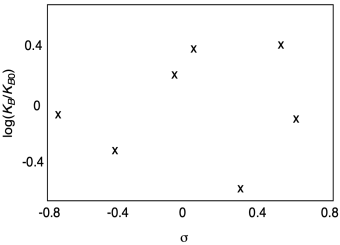
Figure MK14.9. A Hammett plot without a linear free energy relationship.
On the other hand, we might see the relationship break down in a more interesting and informative way. Maybe the graph looks something like this:
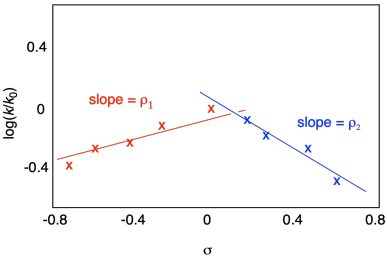
Figure MK14.10. A Hammett plot with two different regimes.
The relationship appears to be linear, but with a bend. We can model this data as the intersection between two different lines. A discontinuity like this can tell us that there's a change in the mechanism at some point. Derivatives along one line follow one mechanism, but derivatives along the other line follow a different mechanism, with a different electron demand.
Problem MK14.1.
Sometimes, correlation with σ fails to yield a linear relationship, but working with the acidity constant of phenol instead of benzoic acid works better. The log of pKa(XC6H4OH)/pKa(C6H5OH) is called σ-. Show stuctures to explain why σ- might respond differently to substituent effects compared to σ.
Problem MK14.2.
Researchers at University of Chicago managed to prepare an alkyl hydrido platinum complex, which underwent reductive elimination when warmed to -25°C.2

When substituted triphenylphosphines (p-X-C6H4)3P were coordinated to the metal, the reaction rate constants varied as follows:
| X | k (s-1) |
| Cl | 9.2 x 10-4 |
| H | 4.5 x 10-4 |
| CH3 | 1.4 x 10-4 |
| CH3O | 4.7 x 10-5 |
Propose a reason for the dependence of the reaction rate on the ancillary ligand.
References Cited
1. Hammett, L. P. The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives. J. Am. Chem. Soc. 1937, 59, 96-103.
2. Abis, L.; Sen, A.; Halpern, J. Intramolecular Reductive Elimination of Alkanes from cis-Hydridoalkylbis(phosphine)platinum(II) Complexes. J. Am. Chem. Soc. 1978, 100, 2915-2916.
This site was written by Chris P. Schaller, Ph.D., retired, College of Saint Benedict / Saint John's University (with contributions from other authors as noted). It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Navigation:
Back to Determination of Mechanism
Back to Structure & Reactivity