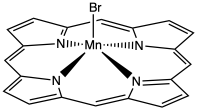
TM7. Geometry in Transition Metal Complexes
If you have studied Lewis structures, then you know that the number of lone pairs and atoms around a specific atoms tells you the geometry at that specific atom. Something very similar is true in coordination complexes, but it's slightly simpler. In transition metal complexes, the lone pairs on the metal do not contribute to its overall geometry. All that matters is the number of ligands attached to the metal.
-
In coordination complexes, the number of ligands determines the geometry.
As a result, there is a pretty straightforward correlation between coordination number (the number of ligands) and geometry.
Table TM7.1. Relationship between the number of donors and the geometry of a complex.
| # ligands | geometry |
| 2 | linear |
| 3 | trigonal planar |
| 4 | tetrahedral; sometimes square planar |
| 5 | trigonal bipyramidal; sometimes square pyramidal |
| 6 | octahedral |
The most common coordination numbers are 4-6, and so the most common geometries are tetrahedral, square planar, trigonal bipyramidal, square pyramidal, and octahedral.

Figure TM6.1. The most common coordination geometries.
There are two possble geometries for coordination number four, and two possible geometries for coordination number five. How do we know which will happen?
For coordination number five, we really can't make an easy prediction. In terms of the angles between ligands, these two possible geometries are really pretty close to each other, so the distinction is subtle. If you call everything that's five-coordinate a trigonal bipyramidal geometry, you will be in the right ballpark. In fact, often the geometry is somewhere in between. It's like trigonal bipyramidal, but the two ligands that should be 180 degrees from each other are bent at a smaller angle. It's like square pyramidal, but two of the ligands are pushed up above the square base of the pyramid.
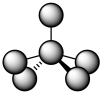
Figure TM6.2. An intermediate geometry, between trigonal bipyramidal and square pyramidal.
Coordination number four is a different story; we do have some predictive ability here. However, there are two different factors that come into play, so there are still some subtle cases.
The first factor is sterics or crowding. In a tetrahedron, the four ligands would be 109 degrees away from each other. In square planar geometry, the four ligands are only 90 degrees away from each other. A tetrahedral geometry is less crowded, and that makes it fairly common.
In order for a square planar geometry to form, there has to be some factor that offsets the steric preference for tetrahedral geometry. There is an electronic destabilization that can happen in tetrahedral geometry, involving electrons that are formally in antibonding orbitals. It can happen in square planar geometry, too, but is not quite so bad when there are eight electrons on the metal. As a result, square planar geometry is most common when the metal has eight electrons.
Problem TM7.1.
Identify the geometry most likely to be adopted by the metal in the following complexes.
a) (Ph3P)3RhCl b) Na[Au(CN)]2 c) (Ph3P)3Rh(H)Cl
d) [Cu(NCCH3)4]PF6 e) Ni(CO)4 f) Ta(OSit-Bu3 )3
g) Fe(CO)4(PPh3) h) K3[Fe(CN)6] i) W(CO)6