Structure & Reactivity

AT.  Historical Overview of the Atom

AT8.  The Aufbau Process and Hund's Rule

   Earlier, we saw that electrons tend to go into unfilled orbitals before pairing up in the same one, provided other orbitals are available at the same energy level.

   This idea is part of Hund's rule.  Hund's rule says, in part, that if you have two electrons, and there are two orbitals available at the same energy level, then one electron will go into each orbital.  It's partly about avoiding electron-electron repulsion that would occur if you put two electrons into the same orbital -- that is, into the exact same region of space. 

Three panels each show a trio of three short lines in a row at the same level. There is a pair of arrows, one up and one down, on the first of the three lines in the panel on the left. This panel has a red X under it. The lines in the middle panel are at a lower level than the lines in the left hand panel. There is an arrow pointing up on the first line and an arrow pointing down on the second line in this group. This panel has a red X under it. The lines in the right hand panel are at a lower level than the lines in the middle panel. There is an arrow pointing up on the first line and an arrow pointing up on the second line in this group. This panel has a green check mark under it.

Figure AT8.1.  Relative energies of three different possible states for two electrons in a p sub-shell.

 

    It's partly something else though, and that is a quantum mechanical bias toward high multiplicity.  Multiplicity refers to the number of unpaired electrons there are in an atom or molecule.  By paired, we mean two electrons that have opposite spin.  Remember, spin is a fundamental quantum mechanical property of an electron.  It can only have two values, and the numerical values seem arbitrary but it's important to know that the two possible options are opposite numbers: they can be either +1/2 or -1/2.  Unpaired electrons would be those that don't have a partner somewhere with an opposite spin value.

   To illustrate that idea, consider the following drawing.  It shows three different ways a set of five electrons might fill in a group of five orbital (maybe the 3d level; suppose these are the valence electrons on a vanadium atom). Often, electrons in orbital diagrams are indicated by arrows, with the direction of the arrow indicating the spin.  An up arrow means spin = 1/2; a down arrow means spin = -1/2.

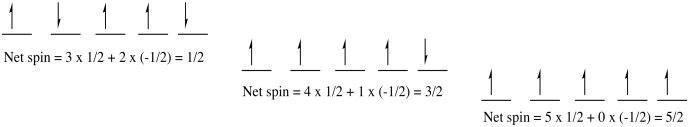
Three panels each show a set of five short lines in a row at the same level. The set of lines on the left is at a higher level than the other two and the set of lines on the right is at a slightly lower level than the other two. There is an arrow on each of the lines in the left panel. Three are pointing up and two are pointing down. Underneath is a label that says net spin equals three times one half, plus two times minus one half equals one half. There is an arrow on each of the lines in the middle panel. Four are pointing up and one is pointing down. Underneath is a label that says net spin equals four times one half, plus one times minus one half equals three halves. There is an arrow on each of the lines in the rigth hand panel. All five are pointing up. Underneath is a label that says net spin equals five times one half equals one.

Figure AT8.2.  Multiplicity illustrated by three of the different possible states for five electrons in a d sub-shell.

 

    In two cases, some of the electrons are paired; they have a partner somewhere with opposite spin.  The multiplicity is basically a tally of how many unpaired electrons are left over; you get the multiplicity by adding up the spin value of all the electrons.  One case has all the electrons unpaired.  All of the electrons have the same spin.  Multiplicity is maximized in this case.  Hund's rule says this case has the lowest energy.

   What about if two electrons occupy the same orbital?  We could still maximize multiplicity by keeping their spins "parallel"; that is, they could both have spin = 1/2 or both spin = -1/2.   That doesn't happen, though.   Remember the quantum rule that no two electrons on the same atom can be described by the same set of quantum numbers.  In other words, each electron on the atom must have a unique identity.  This rule has a name, too: the Pauli exclusion principle. 

 

Problem AT8.1.

Explain the errors in each of the following electron filling diagrams. The 1s level isn't shown to simplify the drawing; just assume it is filled as it should be.

 

This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with contributions from other authors as noted.  It is freely available for educational use.

Creative Commons License Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. 

Send corrections to cschaller@csbsju.edu

 

 

Navigation:

Back to Atoms

Back to Structure

Back to Structure & Reactivity