
AT2. Old Quantum Mechanics: Basic Developments
Today, we know that atoms contain protons, neutrons and electrons. The protons have significant mass and a positive charge and are found in the nucleus of the atom. The neutrons have mass but no charge and are also found in the nucleus. The electrons have negative charge and very little mass and are found outside the atom's nucleus. The weight of an atom in atomic mass units is approximately the sum of its protons and neutrons, since the electrons don't have much mass.
For example, a typical carbon atom has six protons and six neutrons, and it has an atomic weight of 12 amu. A carbon also has six electrons, but they are so small that they don't contribute to carbon's weight.
An element is defined by the number of protons in its nucleus.
The number of protons in an atom is equal to the number of electrons, to balance the charge.
Some carbon atoms have an extra neutron or two, so carbon may have an atomic weight of 13 or even 14 amu. However, a carbon atom can't have an extra proton; an extra proton would make it a nitrogen atom. It is the six protons that make the atom behave like carbon. Many other elements may have slightly different atomic weights, depending on how many neutrons are found in the nucleus. Different atoms of the same element with different weights are called isotopes. For example, 12C, 13C and 14C are all isotopes of carbon. They all have six protons, but different numbers of neutrons, as seen in a model of 12C and 13C, below.

Figure AT2.1. A simple model of two of the isotopes of carbon.
Neutrons are also in the nucleus.
A neutron has a mass similar to a proton, but has no charge.
Compared to protons and neutrons, the mass of an electron is very small.
Problem AT2.1.
An element's atomic number is just the number of protons in an atom of that element. Given the following atomic numbers and atomic weights, identify the number of protons, neutrons and electrons in an atom of the element.
a) oxygen: atomic number = 8, atomic weight = 16
b) phosphorus: atomic number = 15, atomic weight = 31
c) zinc: atomic number = 30, atomic weight = 65
d) gold: atomic number = 79, atomic weight = 197
Problem AT2.2.
If a proton's mass is 1.67 x 10-27 kg and the mass of an electron is 9.11 x 10-31 kg, how many times heavier is a proton than an electron?
Problem AT2.3.
If carbon in nature is about 99% 12C and 1% 13C, then what is the average weight of a carbon atom?
Problem AT2.4.
Note that 14C is even rarer than 13C, because 14C is converted into 14N via radioactive decay. In that event, a high-energy electron is emitted from the 14C nucleus. Explain how that emission must convert the carbon into a nitrogen, and indicate how many protons and neutrons are found in the resulting nucleus.
Problem AT2.5.
Magnesium in nature is found in three major isotopes. It is nearly 79% 24Mg, about 11% 25Mg and 12% 26Mg. What is the average weight of a magnesium atom?
Problem AT2.6.
Chlorine in nature is found in two major isotopes: 35Cl and 37Cl. If the average atomic weight of chlorine is about 35.5, what percentage of each isotope is found in nature?
A number of developments at the beginning of the twentieth century led to our current understanding of the structure of atoms and molecules a hundred years later. At that time, some people though protons, neutrons, and electrons were lumped together in the atom. This view of the atom was called the "pudding model" of the atom.
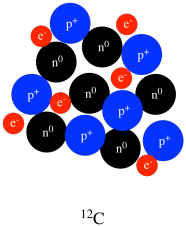
Figure AT2.2. The pudding model of the carbon atom.
Ernest Rutherford first proposed that an atom contains a very small, positively charged nucleus surrounded by empty space. The electrons orbited far away from the nucleus.

Figure AT2.3. Rutherford's model of the atom has electrons in orbit around a dense nucleus.
Rutherford was explaining the result of an experiment in which alpha particles (positively charged helium ions) were fired at a gold foil. Most of these particles passed through the foil easily, suggesting there was a lot of empty space in the material. However, some of the particles bounced directly back, having collided with the small, highly charged nuclei. The positive alpha particles were powerfully repelled by the positive nuclei, because like charges repel each other. He didn't really know much about the location of the electrons, the negatively charged particles in the atom, but believed they orbited the nucleus like planets around the sun.
Why weren't the electrons found in the nucleus? If electrons are attracted to protons, it seems like that's where they should be. Niels Bohr suggested that electrons are found only in specific, allowed orbits at different distances from the nucleus.
That conceptual leap to specific, allowed orbits marks the introduction of quantum mechanics into the understanding of the atom. Quantum mechanics is based on the idea that on a very small scale, many properties only have specific values (like 1, 2, 3...) instead of any value at all (like all the possible fractions between these integers). In other words, in the world around us, we usually view things like walking up a ramp. We can heat a pot of water just a little bit warmer, and just a little bit warmer than that, and so on. On the atomic scale, however, the world is more like walking up a set of stairs. Maybe you could heat the water to 30 oC or 40 oC, but heating to 35 oC would be impossible, because heat only comes in 10 degree packages. That is, in fact, how the quantum world really works, but on the human scale, the steps involved are so tiny that we cannot notice them.

Figure AT2.4. Bohr's model has electrons orbiting at fixed distances from the nucleus.
Bohr's model was also consistent with the earlier idea of the periodic table of the elements. The idea is that electrons are found in different "shells" that are each further and further from the nucleus. Each of those shells corresponds roughly to a different row in the periodic table. Hydrogen and helium have electrons only in the first shell, and we see those two elements in the first row of the periodic table. Carbon and oxygen's outermost electrons are found in the second shell, so they show up in the second row of the periodic table.
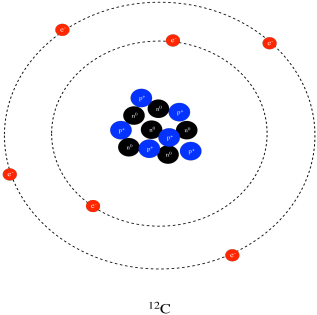
Figure AT2.5. A carbon atom depicted using Bohr's model.
Each row in the periodic table corresponds to an outer layer of electrons that are found further from the nucleus than the outermost electrons in the row before it. We are going to see eventually that there is a further variation on this idea, but it is still pretty much the way we see the periodic table today. Hydrogen starts the first shell, lithium the second, sodium (the Latin, natrium) the third, potassium (Latin, kalium) the fourth, and so on.
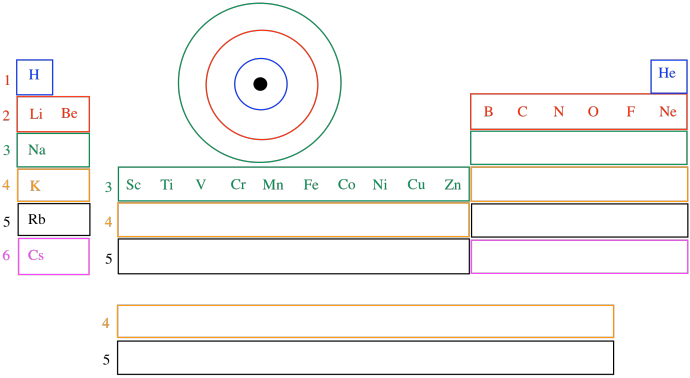
Figure AT2.6. The rows of the periodic table are related to the shells in Bohr's model.
The variation we are going to see involves that dip in the middle of the periodic table. Scandium through zinc have outer electrons that are only in the third shell, not the fourth. The third and the fourth shell overlap a little bit, so that some electrons actually start to go into the fourth shell (as in potassium and calcium), then finish filling the third shell across the transition metals. The reasons for that also have to do with quantum mechanics, but we will need to learn a little more about energy and waves before we see why.
Bohr showed that electrons might be found in specific orbits around the nucleus. He also showed that electrons in these different orbits have specific amounts of energy. By doing this mathematically, he was offering an explanation to an important problem. People knew that atoms can absorb energy (they can be heated in a flame, for example) and give the energy back again in the form of light. Rather than give off light of all colours when excited, atoms only give off very specific colours. For example, heating lithium salts in a flame produces a red colour, but heating sodium salts produces an orange colour, whereas potassium salts produce a purple colour, and so on.
These colours can be separated and studied using a prism. When people did that, they found that a given atom does not produce just one pure colour of light, but several different ones. When separated by a prism, the light given off by an excited compound could be seen against a dark surface as several different, coloured lines. These were called emission lines.
It had been known since the early 1800's that light had wave properties, and that light of different colours had different wavelengths. For example, red light consistes of electromagnetic waves, with a wavelength of about 700 nm, but blue light's wavelength is about 450 nm. That means a colour can actually be measured numerically. Because of that fact, people can look for mathematical relationships between the emission lines observed for different atoms. Those mathematical relationships may reveal something about the atoms themselves.
Furthermore, it was known that different wavelengths of light corresponded to different amounts of energy. In one of the first developments in quantum mechanics, Max Planck in 1900 proposed that light travels in bundles called photons. Although they are particles, these photons do have wave properties. The amount of energy in a photon of light corresponds to its wavelength.
By proposing that electrons could be found only in specific orbits, specific distances away from the nucleus, Bohr was trying to explain observations from atomic spectroscopy reported by another scientist named Rydberg. Rydberg had found a mathematical relationship between the wavelengths of these emission lines. Bohr thought that, when energy was added, electrons could be excited from one energy level (or orbit) to a higher one. When the electron relaxed back to its original orbit, it gave off the energy it had gained in the form of light. The specific emission lines occur because electrons are found at very specific energy levels in an atom, so a drop from one level to another always produces the same amount of light energy. That specific amount of light energy has a specific colour.

Figure AT2.7. The relationship between colour, wavelength, and energy of a photon.
Bohr then used the mathematical relationships describing electrostatic attraction and centripetal force to show that his model of the atom was consistent with Rydberg's relationship. In fact, he could use his model to predict the emission lines of an atom.
Problem AT2.7.
Bohr's explanation of atomic structure built on Rydberg's observation of a numerical series in spectral emission lines. Solving a series involves finding a pattern in numbers. Find the patterns among the following sequences of numbers, and predict the next number in the sequence.
a) 1, 2, 3, 4...
b) 2, 4, 6, 8...
c) 3, 5, 7, 9...
d) 1, 4, 9, 16...
e) 2, 4, 8, 16...
f) 1, 1/2, 1/4, 1/9...
Problem AT2.8.
Bohr's idea depended partly on the use of Coulomb's Law of electrostatic attraction. Coulomb's law is expressed mathematically as follows:
F = (k q1q2 )/ r2
in which F is the attractive force between two charged particles, q1 and q2 are the charges on the two particles, r is the distance between the two particles and k is a constant. A large value of F means that the charges are strongly attracted to each other.
a) Suppose q1 is the charge on the nucleus of an atom and q2 is the charge on an electron. What happens to the force of attraction between an electron and the nucleus when the charge in the nucleus increases? Explain.
b) Suppose r is the distance from the electron to the nucleus. What happens to the force of attraction between an electron and nucleus when the electron gets further from the nucleus?
c) Using the ideas of Coulomb's law, compare the attraction of an electron to the nucleus in a helium atom versus a hydrogen atom.
Problem AT2.9.
Max Planck described the energy of a photon using the following relationship:
E = hν or E = hc/λ
In which E = energy; ν =frequency; λ = wavelength; c = speed of light; h = Planck's constant
a) What happens to the energy of light as its wavelength gets longer?
b) What happens to the energy of light as its frequency gets higher?
Other people were familiar with these ideas and already knew about the relationship between light and energy. Bohr's model of the atoms put all of these ideas together to successfully explain a specific atomic property:
colour = wavelength = energy of light = energy between electron levels.
In other words, an excited electron can drop back to its original orbit by giving off a photon with an energy exactly the same as the difference in energy between the two orbits ("excited state" and "ground state" orbits).

Figure AT2.8. An electron can be thought of as both a particle and a wave.
However, Bohr did not explain why electrons would be found at specific energy levels in the first place. Louis de Broglie, a historian-turned-physicist, solved this problem with the idea of wave-particle duality. de Broglie put together the following ideas:
One way to illustrate why an electron might have only certain allowed orbits is via the "particle in a box", a basic concept from quantum mechanics. If a particle has wave properties, then it has a wavelength. Its wavelength depends on certain conditions. By analogy, if you take a guitar string and attach it to the ends of a box, the string can only vibrate at certain frequencies. That's how guitarists can change the note played on a guitar string. By pressing one end of the string against a fret on the guitar neck, the length of the string is changed, and so is its allowed wavelength, so it makes a different sound.
The string can't move at the two points where it is held. That means the wave has to form in such a way that it returns to the same position at both ends. Because of that, certain wavelengths won't work, because the wave won't be able to return to that correct position at the far end.
Furthermore, the allowed wavelengths of a guitar string also depend on the thickness of the string. As a result, there are two conditions that control the tone that is played: which of the six guitar strings is plucked, and where the string is held against the frets.

Figure AT2.8. Quantized particles behave like standing waves with fixed end points, like a guitar string.
The same thing is true with very small particles that have wave properties. These particles can have only certain wavelengths that fit their surroundings. An electron has some property, analogous to the thickness of a guitar string, that limits its possible wavelengths. Given those limits, there are only certain orbits allowed the electron. If its orbit doesn't have the right circumference, the electron will not be able to form a complete wave along that orbit.
These ideas ushered in a revolution in science. Quantum mechanics is a very powerful tool. It can be used to accurately predict how molecules will behave. Unfortunately, the mathematics involved in quantum mechanics are one or two math courses beyond what most introductory chemistry students are familiar with. Even so, a qualitative feel for some of the consequences of quantum mechanics is important enough that we should explore it.
Problem AT2.10.
Complete the table with the appropriate information.
| Element Symbol | Atomic Number | Mass Number | Number of Protons | Number of Neutrons | Number of Electrons | Charge |
| H | 1 | 1 | ||||
| H | 1 | 0 | ||||
| H | 1 | 2 | ||||
| H | 2 | 1 | ||||
| H | 3 | 1 | ||||
| 4 | 9 | 2 | +2 | |||
| 6 | 12 | 6 | 6 | |||
| 12 | 13 | 12 | 0 | |||
| 43 | 55 | 43 | ||||
| 20 | 40 | +2 | ||||
| Si | 14 | 28 | 0 | |||
| 19 | 28 | +4 | ||||
| Fe | 26 | 30 | 23 | |||
| 35 | 44 | -1 | ||||
| K | 22 | 17 | 21 | |||
| 15 | 15 | 0 | ||||
| 13 | 27 | +3 | ||||
| S | 16 | 16 | 0 | |||
| Pd | 106 | 46 | +1 | |||
| 24 | 28 | 21 | ||||
| 50 | 68 | 50 | ||||
| Hg | 80 | 120 | 79 | |||
| 79 | 118 | 78 |
This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with contributions from other authors as noted. It is freely available for educational use.
 Structure & Reactivity in Organic, Biological and Inorganic Chemistry
by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Structure & Reactivity in Organic, Biological and Inorganic Chemistry
by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
Navigation: