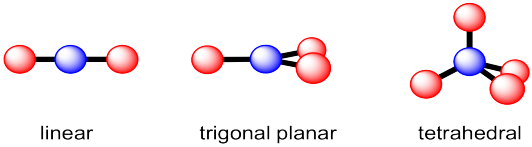
Previously, we looked at a few common geometries of carbon atoms in molecules.  Carbon most often has four neighbouring atoms in the molecule, and in that case it is tetrahedral.  However, sometimes there are only two or three neighbouring atoms, and so linear or trigonal planar geometries are also pretty common.

Figure IM10.1. Three common geometries of a carbon atom.

The term "geometry" often brings to mind angles in shapes such as triangles and squares.  The same aspects of geometry show up in molecules, although we are often concerned with the angles formed at the intersection of two bonds where they meet an atom, rather than the corners of the shapes described by the atoms.  For example, in the trigonal planar geometry shown here, if viewed from above, the three red atoms would form the corners of a triangle. Assuming they are arranged at equal distances around the blue atom, they would form an equilateral triangle.  The angle at each corner would be 60 °,  but from the internal perspective of the molecule, it's more useful to know how widely spaced two red atoms are when they are attached to the same blue atom.  We call this the bond angle; it's the angle formed by going from one of the red atoms to the central blue atom to a second red atom.  That's 120 °.  By comparison, in the linear structure, two red atoms are found 180 ° apart, so the atoms are spaced a little farther apart in the linear structure than in the trigonal planar structure.  In the tetrahedral structure, the angle between two of the bonds between the blue atom and any two red atoms is always 109.5 °.    It makes sense that as more atoms are attached to the central atom, they crowd a little more closely together, so the angle between them gets smaller.

 These geometries are found throughout the periodic table for atoms that have 2, 3 or 4 neighbouring atoms within a molecule.  However, there are also some other molecular geometries that are pretty common.

Earlier, we looked at the environments of atoms or ions within solid structures and considered the "coordination number" of the atom or ion.  Remember, the coordination number is just the number of atoms in close contact with a central atom.  We can think about the geometry around a particular atom in a molecule the same way.

Coordination number 4

 There are actually two different geometric options that occur with some regularity for coordination number 4.  Tetrahedral geometry, which we have seen, maximizes the distances between neighbours.  That could be advantageous because it minimizes crowding.  In fact, tetrahedral geometry is the most common geometry for tjis coordination number.  However, a second geometry is available for a limited number of compounds.  In square planar geometry, all four neighbours are found in the same plane and are roughly 90 degrees apart from each other.  This geometry is most often observed for certain compounds of palladium and platinum as well as a few other transition metals.

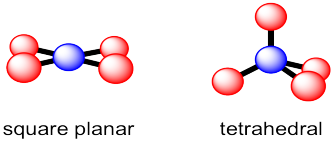
Figure IM10.2. Two common four-coordinate geometries.

  Note that the bond angles in a square planar geometry are not the same as in a tetrahedron.  In a tetrahedron, the four red atoms are arranged in three dimensions around the central blue atom.  They are around 109 ° apart.   In a squre planar geometry, those four atoms all share the same plane.  That puts them all a little closer to each other.  Now they are all 90 °  apart.  So, a tetrahedral geometry is described as having 109 ° bond angles but a square planar geometry is described as having 90 ° bond angles.

• Tetrahedral geometry is the most common shape when a central atom makes four bonds.
• Sometimes, a central atom with four bonds makes a square planar geometry.

Coordination number 5

 In the case of five neighboring atoms, there are two geometries that are roughly equally prevalent.  In a trigonal bipyramidal structure, the central atom is surrounded by three neighbours that form a trigonal plane around it.  The last two neighbours are above and below this plane.  These two neighbours are roughly colinear with the central atom.  The trigonal planar positions referred to as "equatorial"; the other two positions are called "axial".

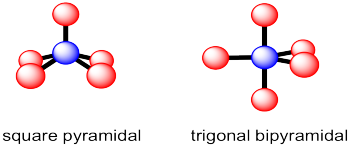
Figure IM10.3. Two common five-coordinate geometries.

The other common five coordinate geometry is square pyramidal.  In this case, the central atom sits above a base of four neighbors; those four positions form a square plane together.  A fifth atom occupies the space above the central atom.

The bond angles in these two geometries are slightly more complicated than in the earlier cases.  In an ideal square pyramid, there would be a square planar base with one central atom (blue) and four atoms arranged around it at 90 °.  In addition, there would be a fifth atom forming the top point or the apex of the pyramid.   It would be straight above the blue atom and at 90 ° to all of the other atoms. However, this ideal geometry is not usually seen because there is a lot of space underneath the pyramid. The base layer of atoms (the basal atoms) push down a little bit into that open space. In doing so, they all get slightly closer to each other, but quite a bit farther from that atom at the apex (the apical atom). That arrangement slightly reduces overall crowding. The exact angles will vary from one case to another. Just to give an example, in the [Ni(CN)₅]^3- anion, the angles between the basal CN groups are around 88 °, whereas the angle between the apical CN group and any of the basal ones is around 100 °.

  Trigonal bipyramidal geometry can be thought of as a case in which this need to relieve crowding by moving into the open space under the square plane at the bottom of the pyramid has resulted in a very different shape.  In this case, two of the basal atoms opposite each other have both dropped way down into that open space to get further away from the other three red atoms. In the drawing above, it's as if we started with a square pyramid sitting on its side, with the apical atom pointing to the left, and pushed two of the basal atoms to the open space on the right.  As a result, we end up with atoms in two distinct positions.  Three of the atoms form a trigonal plane.  They are 120 ° apart from each other. These three atoms are described as the equatorial atoms. The other two atoms are directly across from each other. By themselves, these two would form a linear geometry and would be 180 ° apart from each other. These two atoms are called the apical atoms in this geometry. They are 90 ° from those three equatorial atoms.  

• A central atom with five bonds could form a square pyramidal or a trigonal bipyramidal geometry.
• It is difficult to predict which geometry will occur in a specific case.

Coordination number 6

Almost all examples of atoms with coordination number six can be described as having an octahedral geometry.  Four of the neighbours form a square plane around the central atom, with one atom above this plane and one below it.  As with the trigonal bipyramid, these positions can be described as equatorial and axial, respectively.

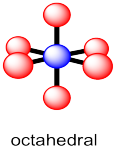
Figure IM10.4. Octahedral geometry.

 The relationships in octahedral geometry are more uniform than in five-coordinate geometry. Each of the red atoms is 90 ° from each of its four nearest neighbours. It also has one far atom that is 180 ° away from itself.

• A central atom with six bonds forms an octahedral geometry.

Electronic vs. molecular geometry

There is a striking difference between geometries around transition metals, in the middle of the periodic table, compared to main group p-block elements, in the right hand part of the periodic table.  The geometry around a transition metal is simply based on the number of atoms bonded to it.  Each surrounding atom takes up some space and so a geometry is adopted to give those atoms roughly equal space around the central atom.

In the p-block, things are sometimes quite different.  It's not just the neighbouring atoms that take up space; the valence electrons on the central atom also have to be accommodated.  Thus, in ammonia, NH₃, we need to consider not just the three hydrogen atoms that are bonded to the nitrogen, but nitrogen's own lone pair as well, in order to determine the geometry.  That's four objects to fit around the nitrogen atom.  The normal geometry for four things is tetrahedral.  Thus, ammonia takes on a tetrahedral shape.  It isn't trigonal planar.

That's sometimes called the overall electronic geometry.  It is the geometry of everything, including lone pair electrons.  To see the relationship between the atoms -- the nitrogen and its three nieghbouring hydrogens -- just ignore the electron pair for a minute.  The nitrogen sits above a trigonal base of three hydrogen atoms.  The molecular geometry -- that shape formed by the nitrogen and the three hydrogens -- is pyramidal.

Figure IM10.5. Trigonal pyramidal geometry.

This phenomenon, in which the geometric relationship between atoms is influenced by where the electrons are on a central atom, is pretty common around chalcogens and pnictogens -- that is, oxygen and the other atoms in its column of the periodic table, as well as nitrogen and the other atoms in its group.  In those cases, lone pairs appear to force the surrounding atoms a little closer to each other.

• If an atom has its frontier electrons (last-filled electrons) in a p orbital, it is a p-block element.
• In a p-block element, both lone pairs and bonds are considered as part of the "electronic geometry".
• The "molecular geometry" is determined by the electronic geometry, with spaces left for the lone pairs.

Problem IM10.1.

Suppose a compound had a central atom surrounded by six groups, including bonds to other atoms as well as its own lone pairs.

a)  What is its overall "electronic" geometry?

b)  What would be its molecular geometry if it had one lone pair?

c)  What would be its molecular geometry if it had two lone pairs?

Problem IM10.2.

 Suppose a compound had a central atom surrounded by five groups, including bonds to other atoms as well as its own lone pairs.

a)  What is its overall "electronic" geometry?

b)  What would be its molecular geometry if it had one lone pair?

c)  What would be its molecular geometry if it had two lone pairs?

Problem IM10.3.

Draw structures for the following compounds.

a)  H₂O        b)  (CH₃)₃O⁺        c)  PCl₃        d)  SF₄        e)  ClF₃        f)  PCl₅

g)  SF₆        h)  ClF₅        i)  XeF₄

Problem IM10.4.

What is the molecular geometry of each of the compounds in problem IM10.3?

Some common geometries are summarized in the table below.

Table IM10.1. Some common (and less common) geometries.

In cases where the molecular geometry is different from the electronic geometry, we sometimes need to make choices about which position a lone pair is more likely to occupy.  The general rule is that lone pairs occupy the less crowded site.  It is as if the lone pair takes up more space than a bond to an atom.  That might seem surprising, because it leaves the atoms in the molecule crowded together.  Although these cases are not very common, they are observed in a number of compounds from the p-block.  Some examples are summarized in the table below.

Table IM10.2. Some unusual geometries.

Problem IM10.5.

Draw structures for the following compounds.

a) IBr    b) ICl₃    c)  ClF₅    d) BrF₃  e) SeF₄    f) IOF₃     g) ArF₄

Problem IM10.6.

Occasionally, atoms can have an even higher number of bonds than we have seen so far.  Predict a reasonable geometry for iodine heptafluoride, IF₇.

This site is written and maintained by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (with contributions from other authors as noted).  It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. 

Send corrections to cschaller@csbsju.edu