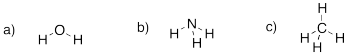
Structure & Reactivity in Chemistry
Introduction to Molecules
IM16. Solutions to Selected Problems
Problem IM1.1.
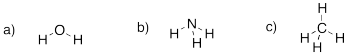
Problem IM1.2.
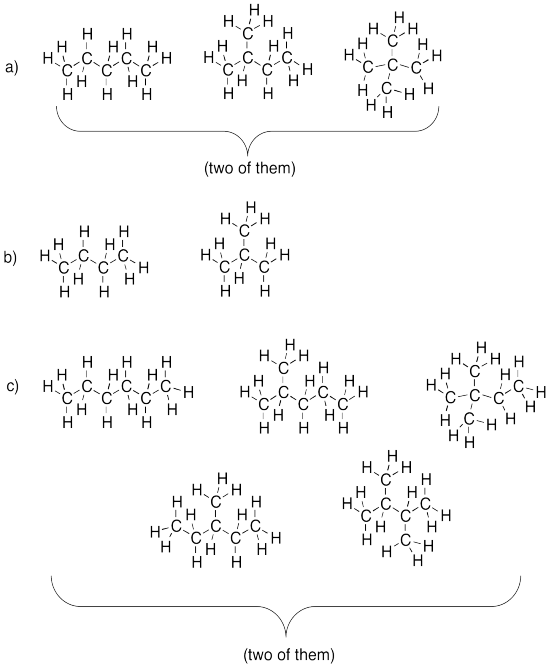
Problem IM2.1.
![]()
Problem IM2.2.
![]()
Problem IM3.1.

Problem IM3.2.
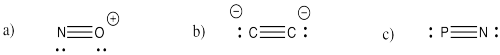
Problem IM3.3.
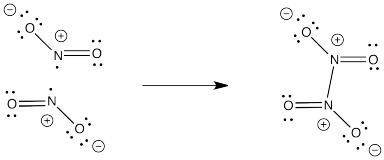
Problem IM3.4.
NO2- would not have an unpaired electron so it would not dimerize like NO2.
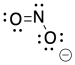
Problem IM4.1.

Problem IM4.2.
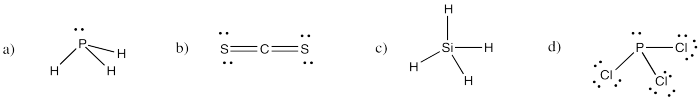
Problem IM4.3.
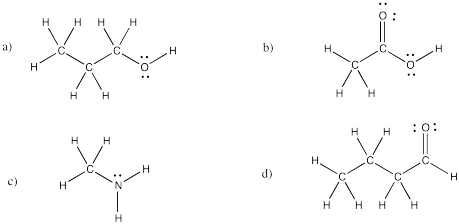
Problem IM4.4.
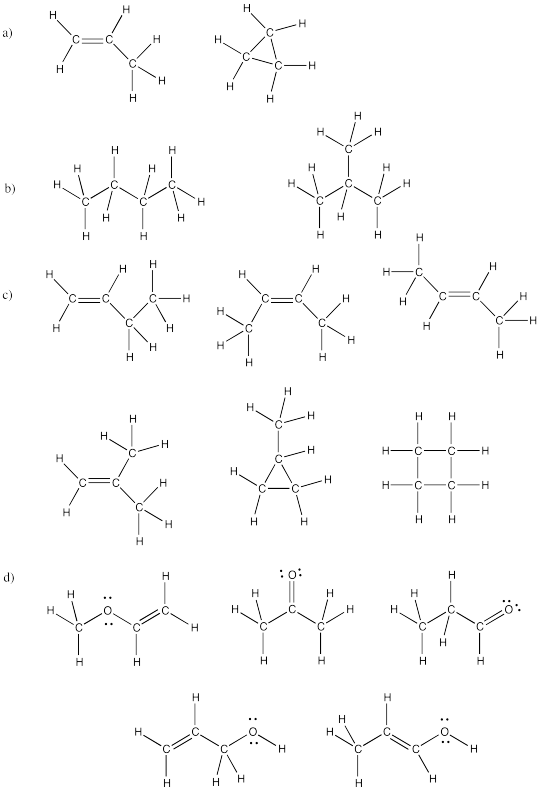
Problem IM4.5.
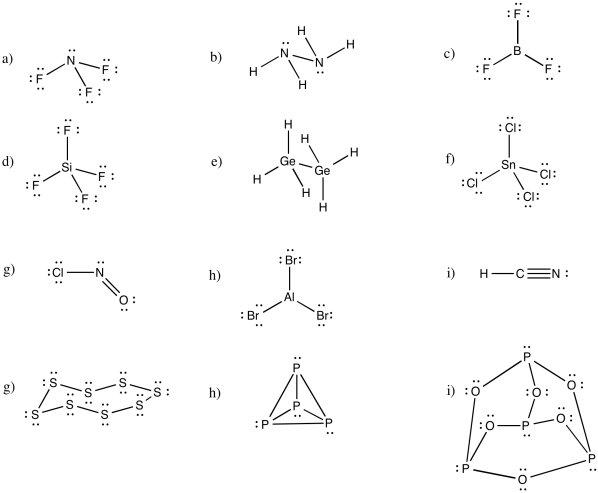
Problem IM5.1.
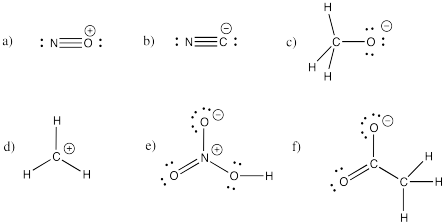
Problem IM5.2.
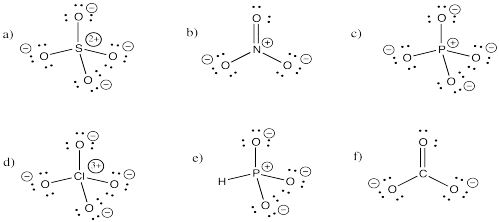
Problem IM5.3.
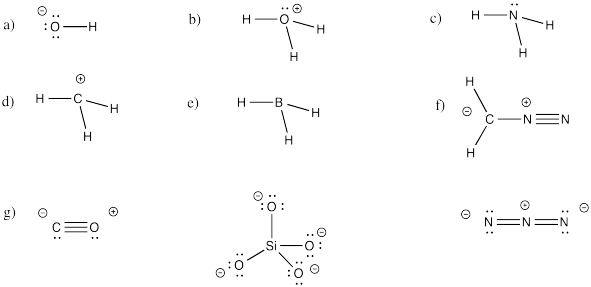
Problem IM5.4.
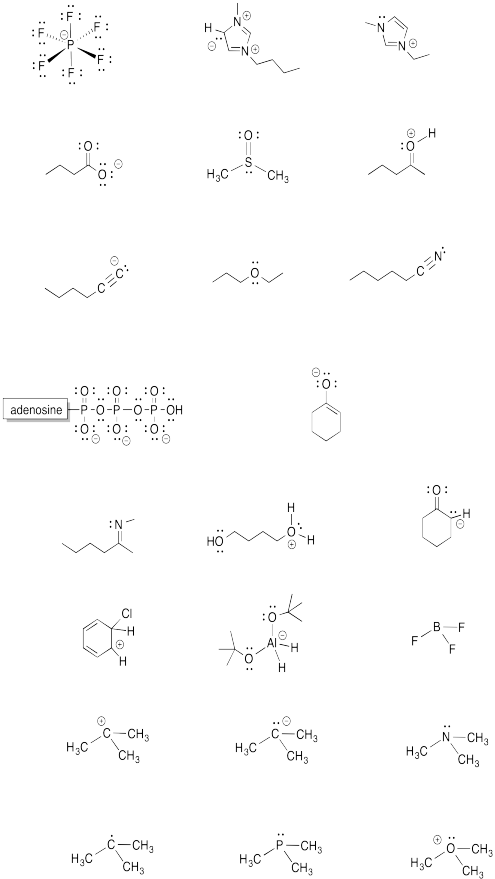
Problem IM5.5.

Problem IM5.6.
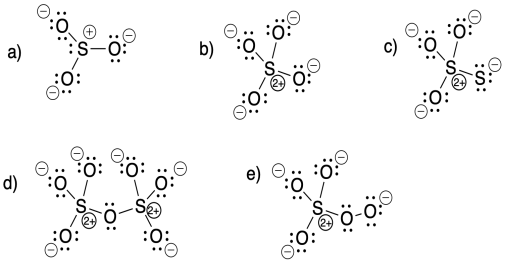
Problem IM5.7.
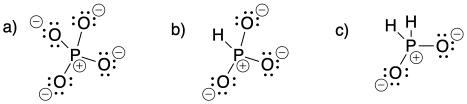
Problem IM6.1.
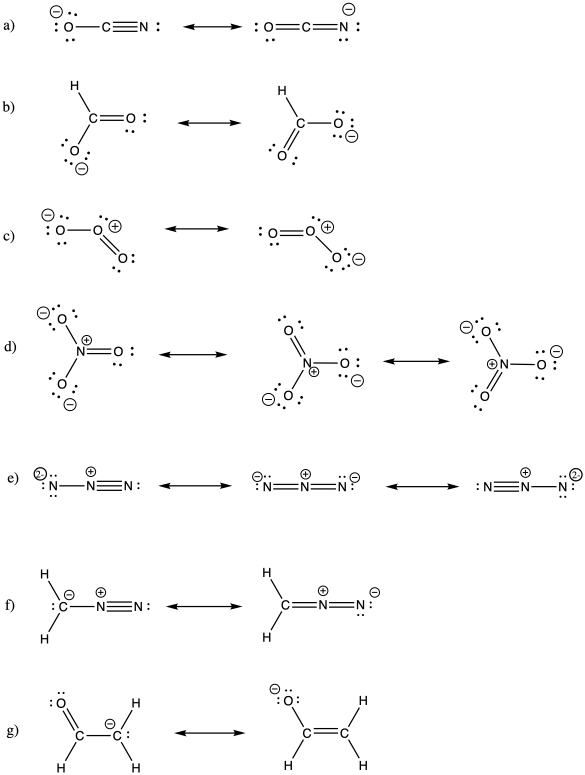
Problem IM6.2.

Problem IM6.3.
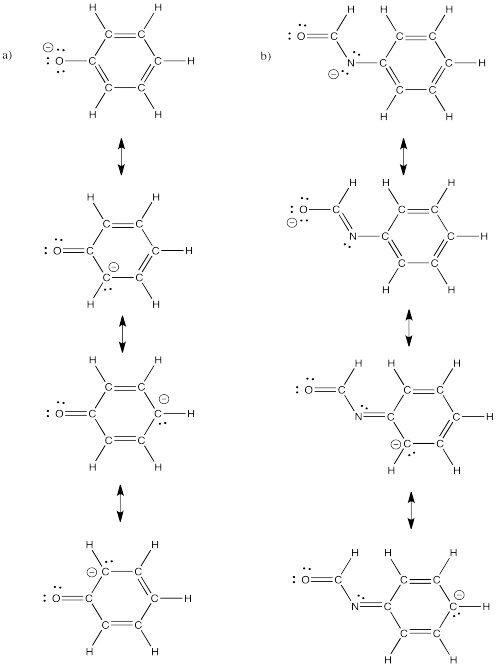
Problem IM6.4.
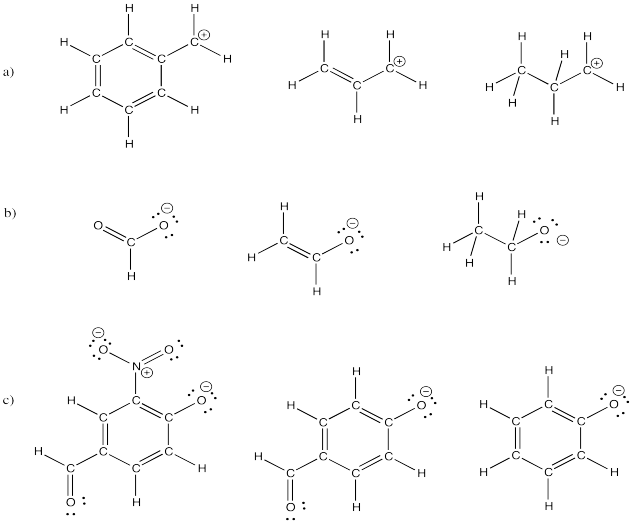
Problem IM6.5.
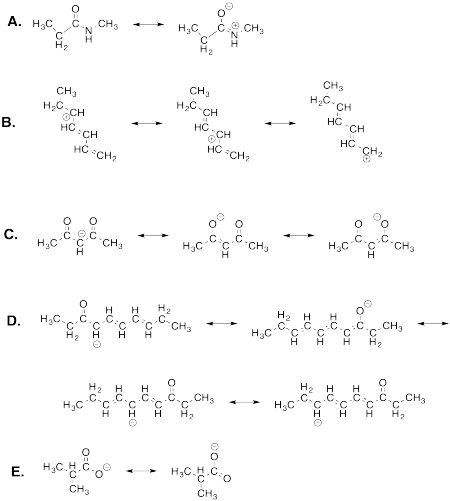
Problem IM7.1.
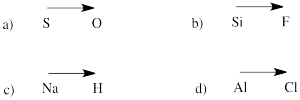
Problem IM7.2.
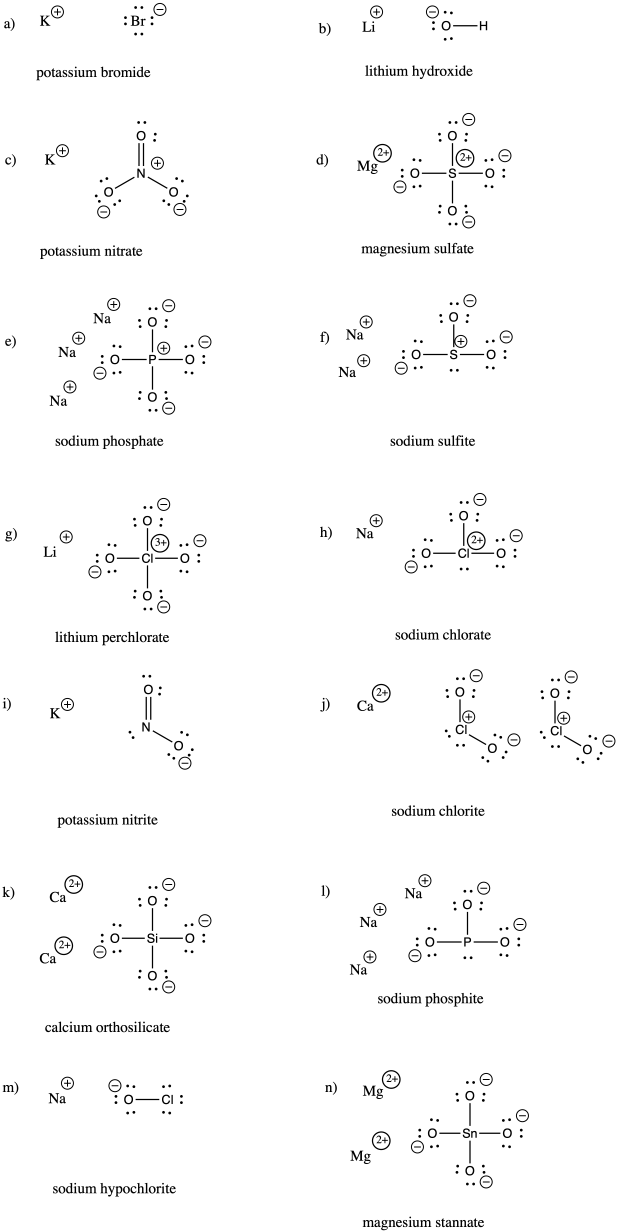
Problem IM7.3.
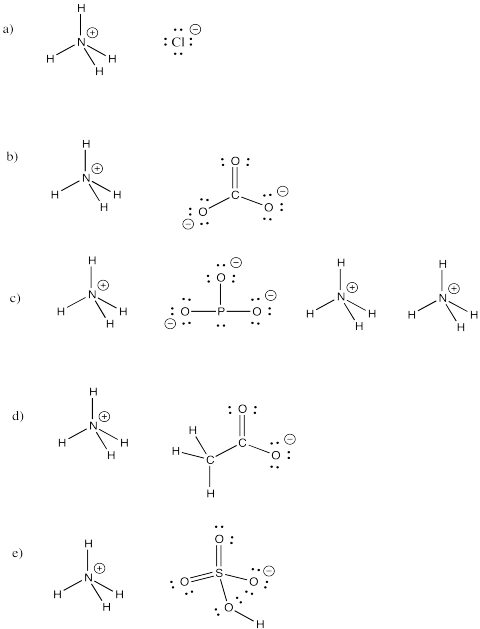
Problem IM7.4.
a) bromide b) oxide c) fluoride d) carbonate e) nitrate f) nitrite
g) sulfide h) sulfate i) sulfite j) persulfate k) carbide l) nitride m) arsenide
n) phosphate o) phosphite p) iodide q) iodate r) periodate
Problem IM7.5.1.
a) i. BH3, electronegativity difference = 0.16; predict non-polar covalent ii. gas phase at room temperature = probably covalent molecule
b) i. KCl, electronegativity difference = 2.34; predict ionic ii. water-soluble solid = probably ionic
c) i. BF3, electronegativity difference = 1.94; predict ionic ii. gas phase at room temperature = probably covalent molecule
d) i. LiBr, electronegativity difference = 1.68; predict polar covalent ii. water-soluble solid = probably ionic
e) i. CaF2, electronegativity difference = 2.98; predict ionic ii. melts above 1000°C = probably ionic
f) i. SnCl4, electronegativity difference = 1.20; predict covalent ii. melts around 240°C = probably covalent molecule
g) i. SnF2, electronegativity difference = 2.02; predict ionic ii. gas above 850°C = probably covalent molecule
h) i. InF3, electronegativity difference = 2.20; predict ionic ii. melts above 1000°C = probably ionic
i) i. InCl3, electronegativity difference = 1.38; predict covalent ii. gas above 800°C = probably covalent molecule
Problem IM8.1.
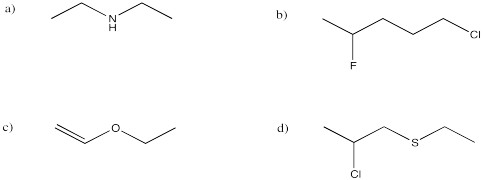
Problem IM8.2.
a) (CH3)2CHCH2CH2CN b) CH3CH2CH(OH)CH3
c) (CH3)2CHCOCH2CH3 d) CH3CH2CONHCH2CH3
Problem IM8.3.
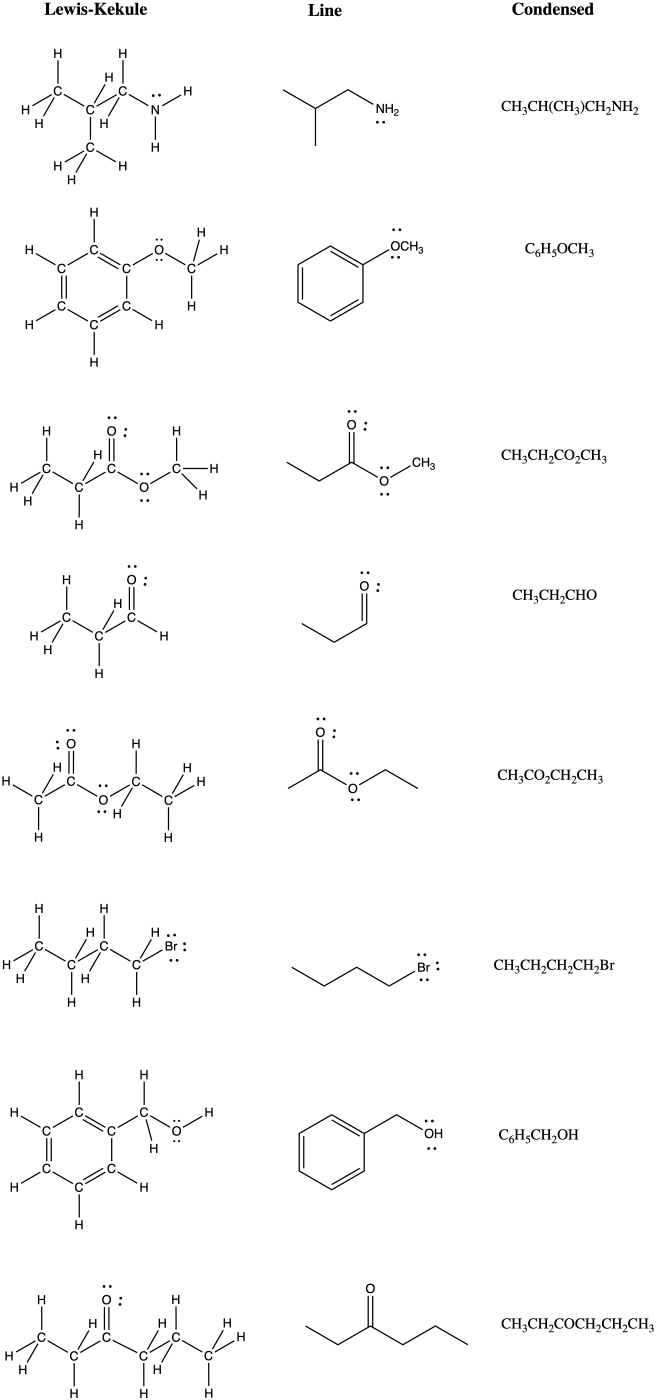
Problem IM8.4.
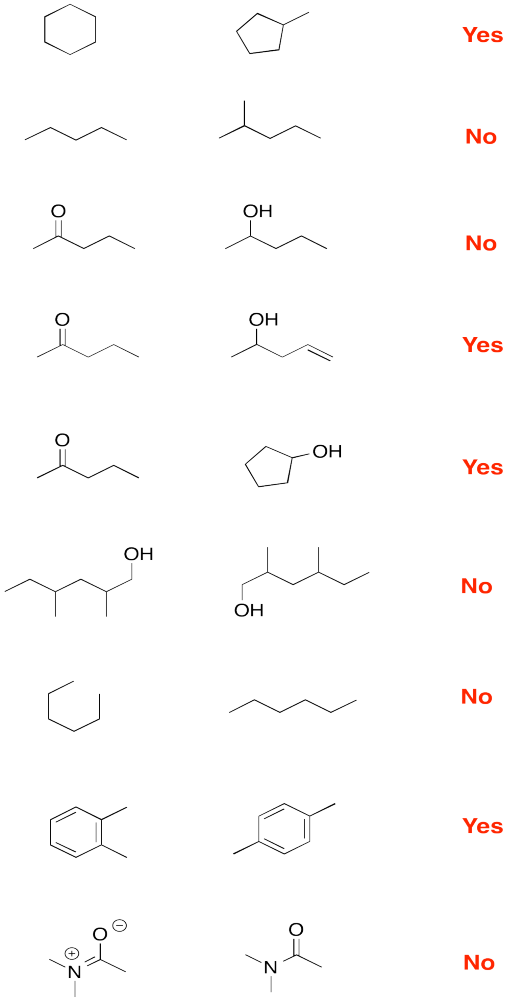
Problem IM9.1.

Problem IM9.2.
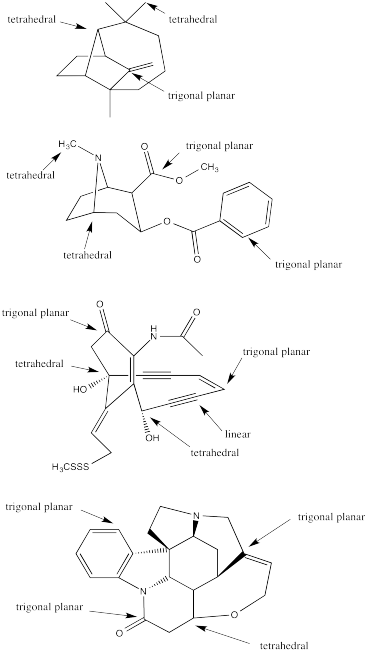
Problem IM10.1.
a) octahedral.
b)
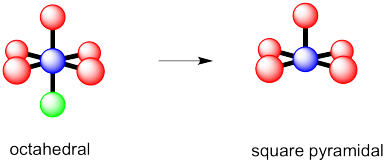
c)
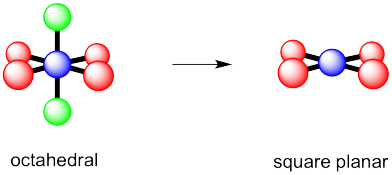
Problem 10.2.
a) trigonal bipyramidal
b) This time there could be two different answers.
If the lone pair occupies one of the axial positions, it would be pretty close to three other atoms.
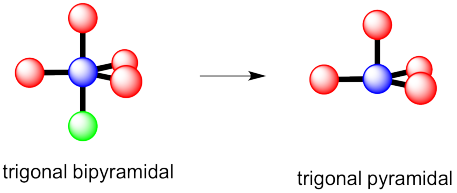
If the lone pairs occupies one of the equatorial positions, it would be pretty close to only two other atoms. The other equatorial atoms are pretty far away.

The rule is that the lone pair goes in the less crowded position, so this molecule would be see-saw shaped.
c) Again, there are two possible geometries. One of them would be trigonal planar, a pretty common geometry.
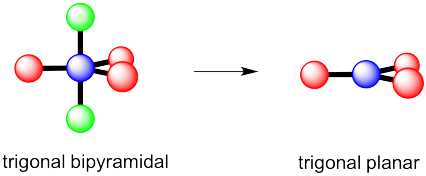
However, that places the lone pairs in the more crowded positions. Instead, the molecule is going to be tee shaped.
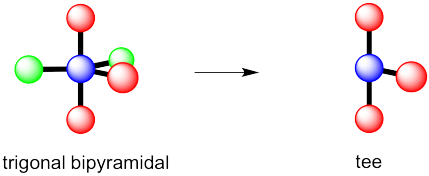
Problem IM10.3.
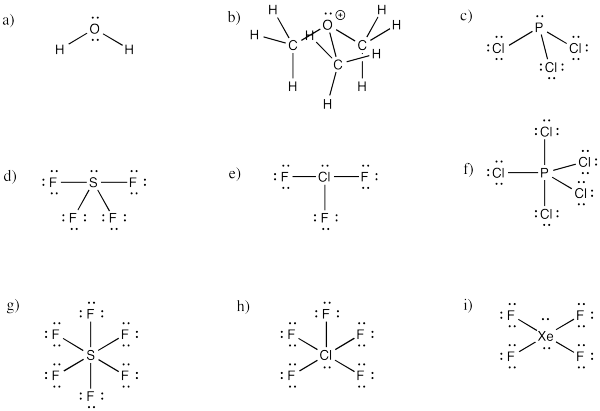
Problem IM10.4.
a) bent b) pyramidal at O, although tetrahedral at C c) pyramidal
d) see-saw e) tee f) trigonal bipyramidal
g) octahedral h) square pyramidal i) square planar
Problem IM10.5.
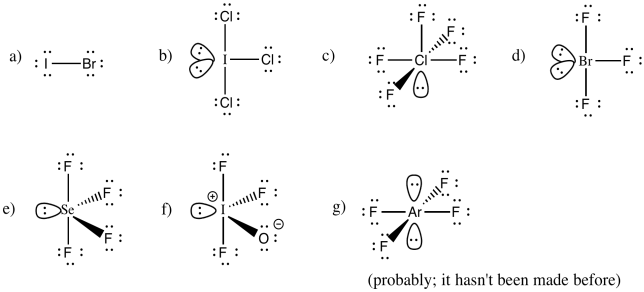
Problem IM10.6.
You may be able to imagine some other possibilites for this number of neighbours, but IF7 adopts a pentagonal bipyramid shape.
Problem IM11.1.
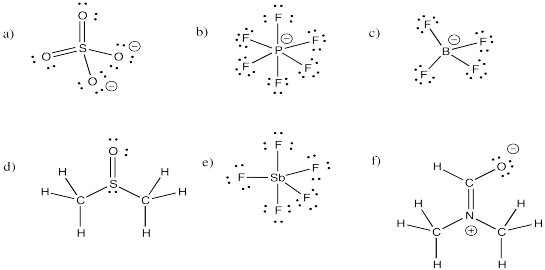
Problem IM11.2.
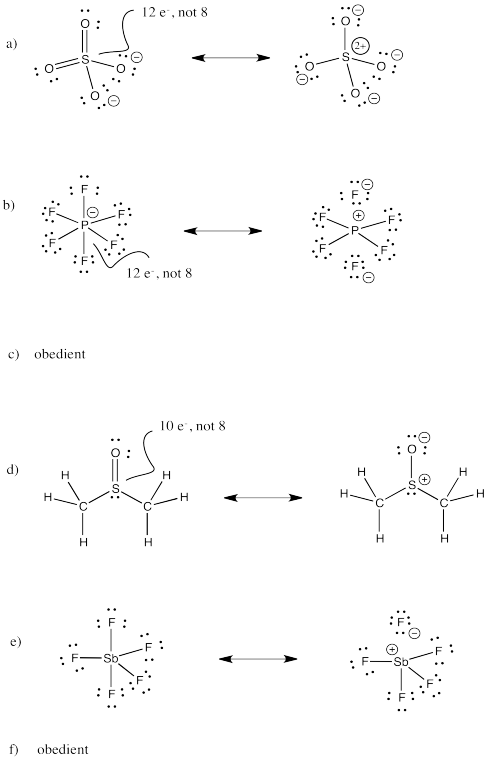
Problem IM11.3.
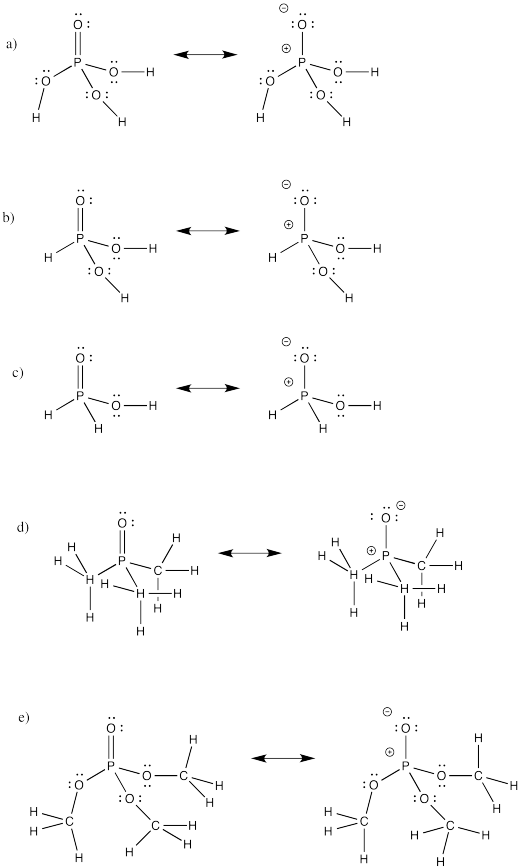
Problem IM12.2.
a) propane b) pentane c) hexane
Problem IM12.3.
a) 3-methylhexane b) 2,2-dimethylpentane c) 2,3-dimethylbutane
d) 2,2,3,3-tetramethylpentane e) 3,5-dimethylheptane f) 4-ethyl-3,6-dimethyloctane
Problem IM12.4.
a) cyclopentane b) cyclohexane c) cyclooctane
d) methylcyclobutane e) 1,1,3-trimethylcyclopentane f) 1,3-dimethylcycloheptane
Problem IM12.5.
a) 1-hexene b) 2-methyl-2-pentene c) 1-methylcyclohexene d) 2,4,6-trimethyl-2-heptene
Problem IM12.6.
a) cyclopentene b) 1,1-dimethylcyclohexane c) 3-hexyne
d) 4-methylcyclohexene e) 1-hexyne
Problem IM12.7.
a) tetrahedral b) trigonal planar c) linear
Problem IM12.8.
a) methylbenzene b) propylbenzene c) 1,2-dimethylbenzene or o-dimethylbenzene (also o-xylene)
d) 1,3-dimethylbenzene or m-dimethylbenzene (also m-xylene) e) 1,4-diethylbenzene or p-diethylbenzene
f) 2-ethyl-1,4-dimethylbenzene
Problem IM12.9.
a) 2,2-dimethylhexanal b) 2-methylcyclopentanone
c) 3-nonanone d) 2,4-dimethyl-2-hexenal
Problem IM12.10.
a) butyl propanoate b) N,N-diethylbutanamide
c) 6-methylheptanoic acid d) 4-pentenoic acid
Problem IM12.11.
a) 1-chloro-2-methylcyclohexane b) cyclooctanol c) ethyl cyclopentyl ether
d) N-propylcyclohexylamine e), 5,5-dimethylheptan-2-ol f) 3-bromo-4,4-dimethyloctane
g) dibutylamine i) methyl phenyl ether (or anisole) j) ethane thiol k) diethyl thioether
l) triethylphosphine m) butanenitrile n) nitromethane
Note that sometimes a number is located directly in front of the suffix for the group to which it refers.
Problem IM12.12
a) benzene (or aromatic), ketone and ether
b) bromide, amine and aldehyde
c) alcohol, thiol and ester
d) thioether, amide and alkene
e) alkyne, alcohol and carboxylic acid
Problem IM12.13.
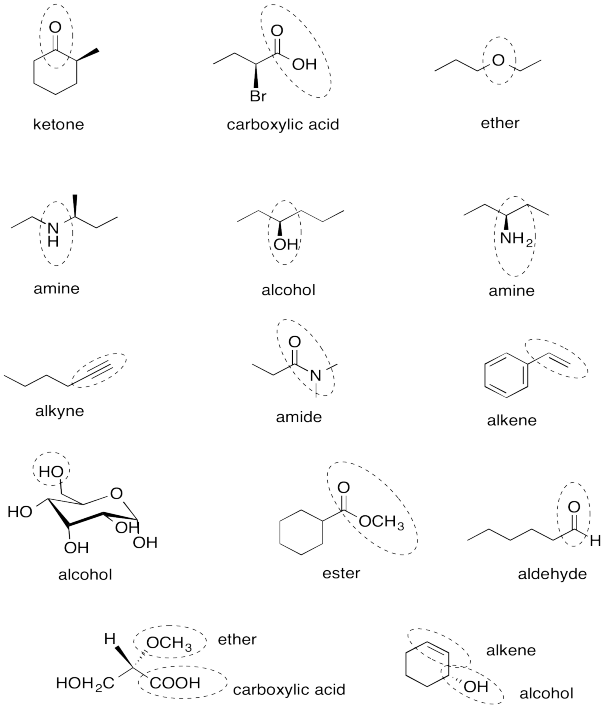
Problem IM12.14.
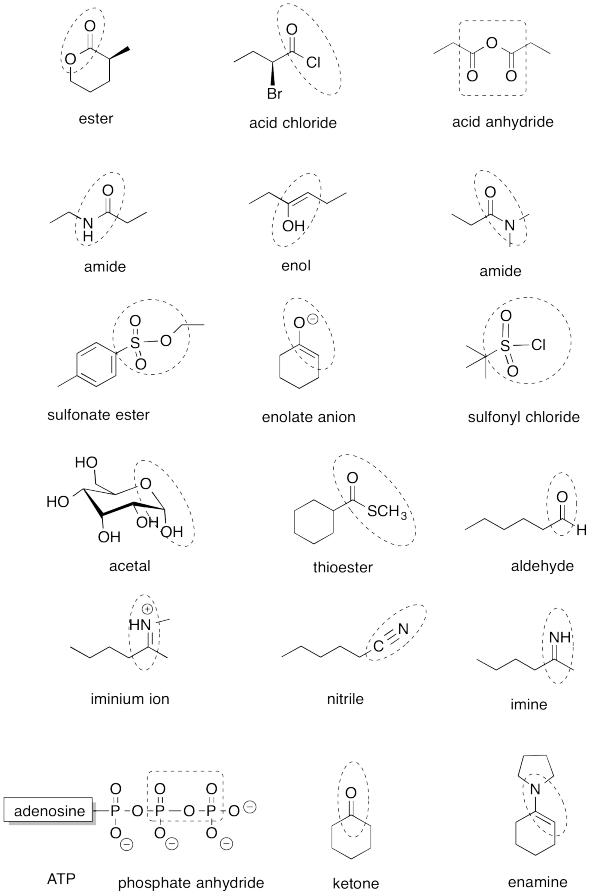
Problem IM13.1.
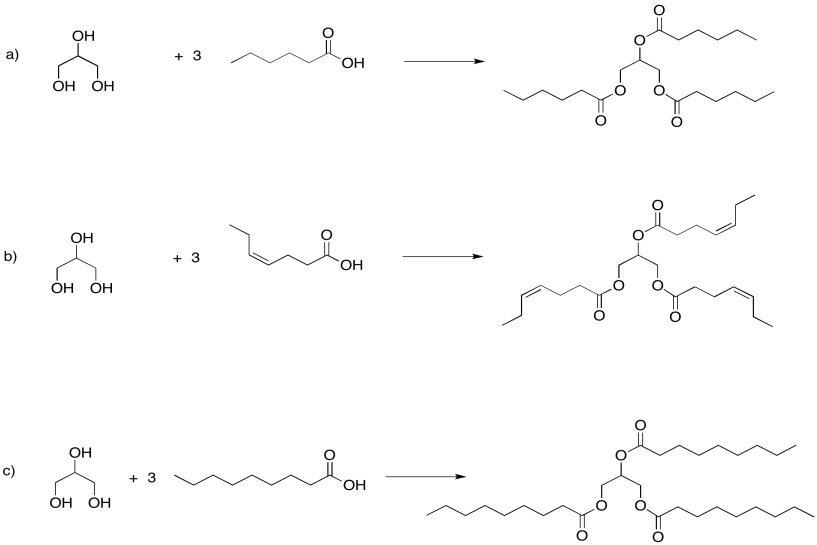
Problem IM13.2.

Problem IM13.3.
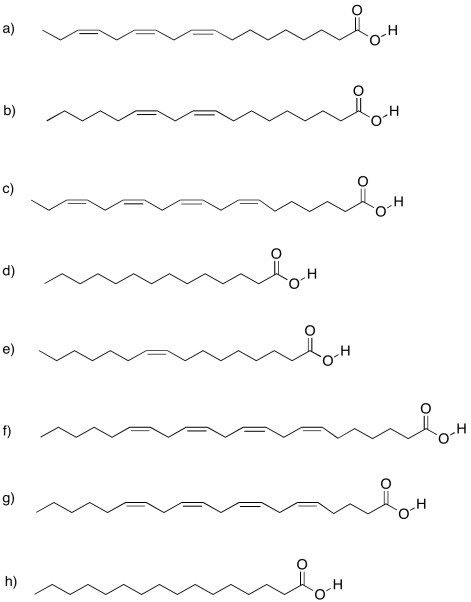
Problem IM13.4.
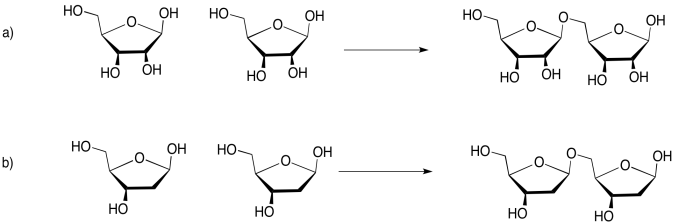
Problem IM13.5.
If you don't know what the wedged and dashed lines in the drawing mean, don't worry about it. They just represent different orientations in space. You will learn about these representations in a later topic called "stereochemistry".
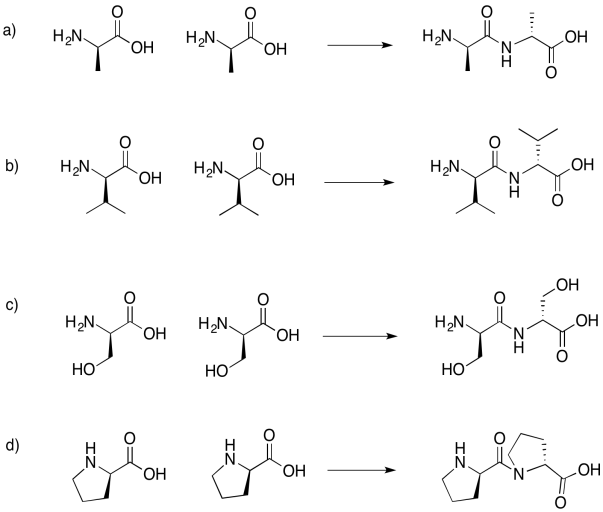
Problem IM13.6.
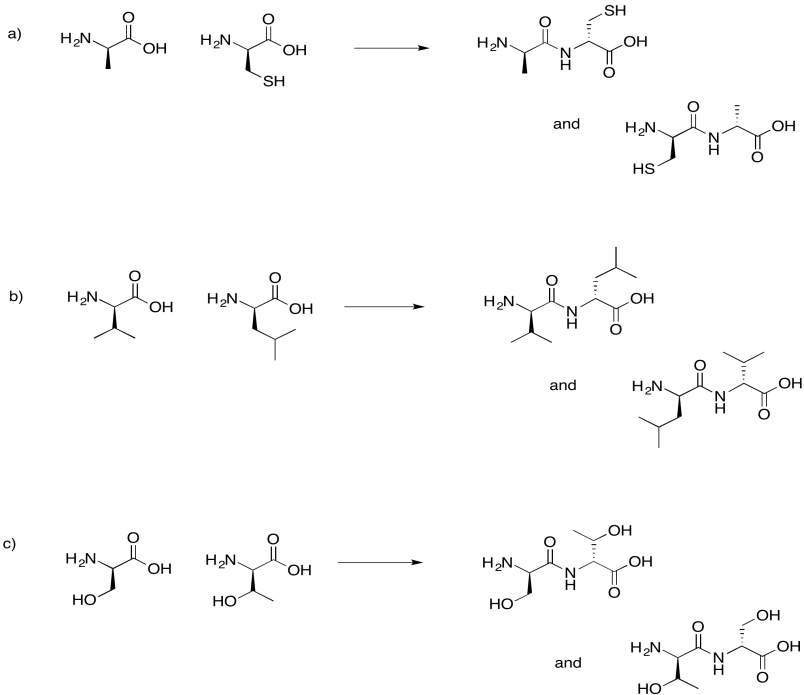
Problem IM13.7.
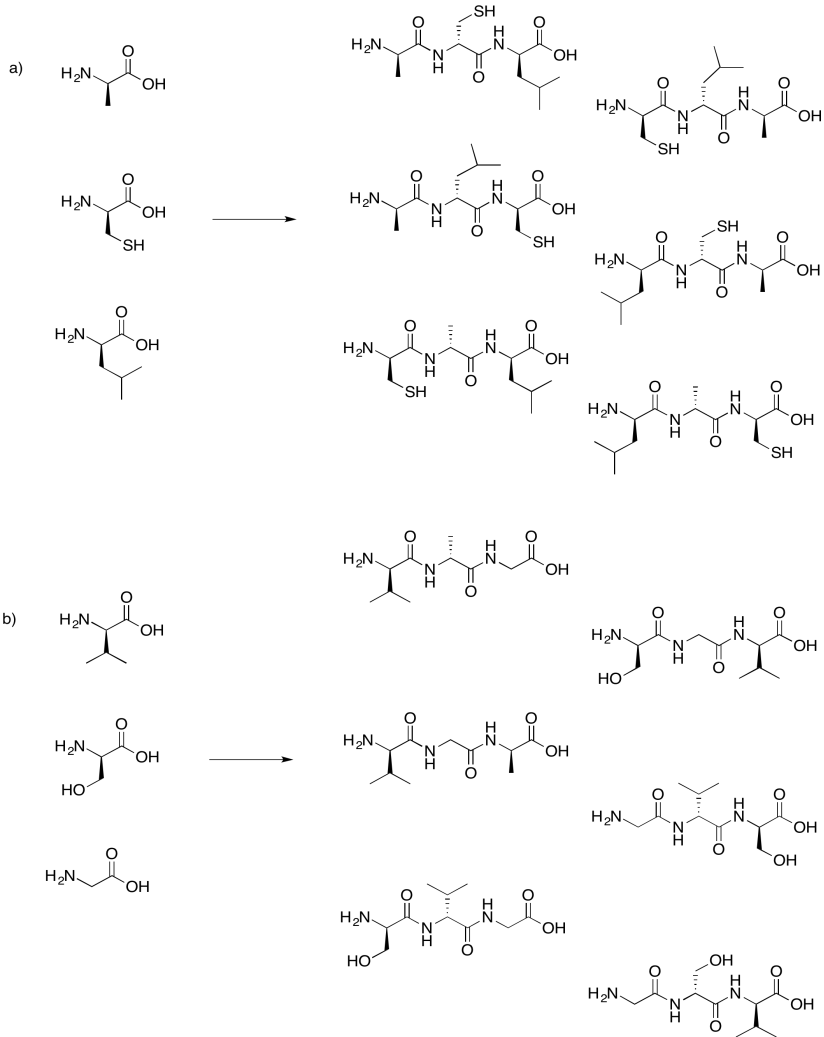
Problem IM13.8.
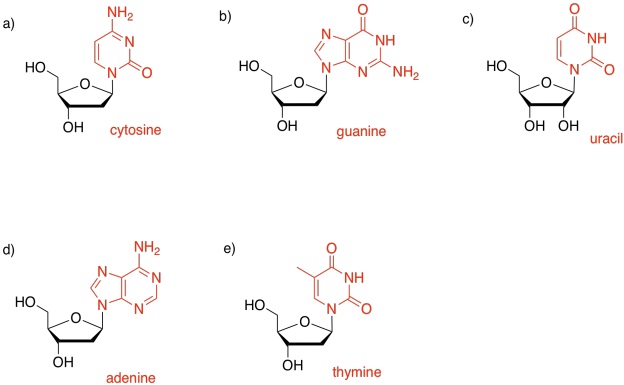
Problem IM15.1.
a) N3- would get to a noble gas configuration.
b) Ta3+ would balance the charge in TaN.
c)

d)

e) #Ta = (1/6)(1/2)(4) for the acute corners and (1/3)(1/2)(4) for the obtuse corners = 4/12 + 4/6 = 4/12 + 8/12 = 1
(note that it's the same outcome as the corners of a cube)
f) #N = (1/4)(8) for the edges and (1/2)(2) for the faces = 2 + 1 = 3
g) Need 2 more Ta.

h) Each tantalum has three nitrogens above and three below it. It's almost octahedral, but the top layer of nitrogens is lined up above the bottom layer rather than being twisted 120 degrees to form an octahedron. The geometry is a trigonal prism.
i)

j)
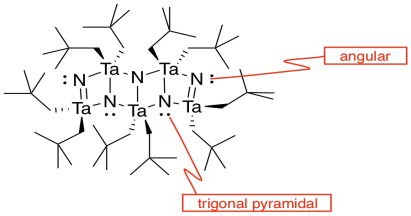
k)
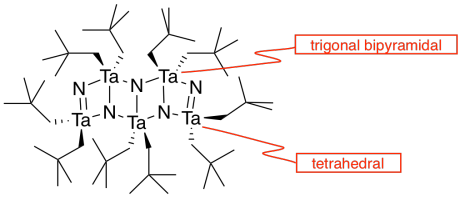
l) The double bonds hold the atoms more closely together than the single bonds.
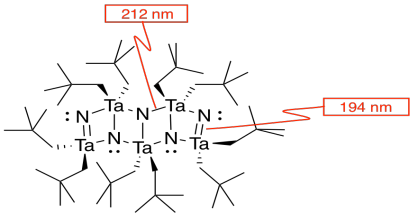
m) You can imagine the molecules stacking together to make a cubic array of TaN.

This site is written and maintained by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (with contributions from other authors as noted). It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
Back to Introduction to Molecules
Back to Web Materials on Structure & Reactivity in Chemistry