Structure & Reactivity
Nuclear Magnetic Resonance Spectroscopy
NMR18. Solutions to Selected Problems.
Problem NMR2.1.
a) 10 ppm
b) 64 ppm c) 158 ppm
Problem NMR2.2.
a) 63 ppm b)
201 ppm c) 71 ppm
Problem NMR3.1.
Problem NMR3.2.
a) pentane, CH3CH2CH2CH2CH3,
or hexane,
CH3CH2CH2CH2CH2CH3
b) heptane, CH3CH2CH2CH2CH2CH2CH3,
or octane, CH3CH2CH2CH2CH2CH2CH2CH3
c) nonane, CH3CH2CH2CH2CH2CH2CH2CH2CH3,
or decane, CH3CH2CH2CH2CH2CH2CH2CH2CH2CH3
Problem NMR4.1.
Problem NMR4.2.
a) sp3 b) sp2
c)
sp2 d) sp3
e) sp3 f) sp2
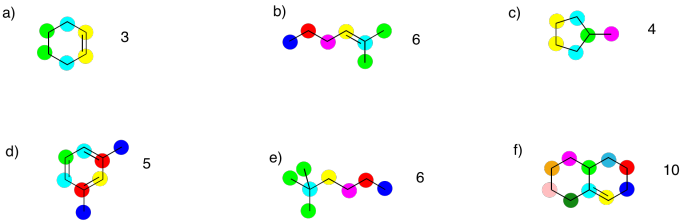
Problem NMR5.1.
Problem NMR5.2.
Problem NMR6.1.
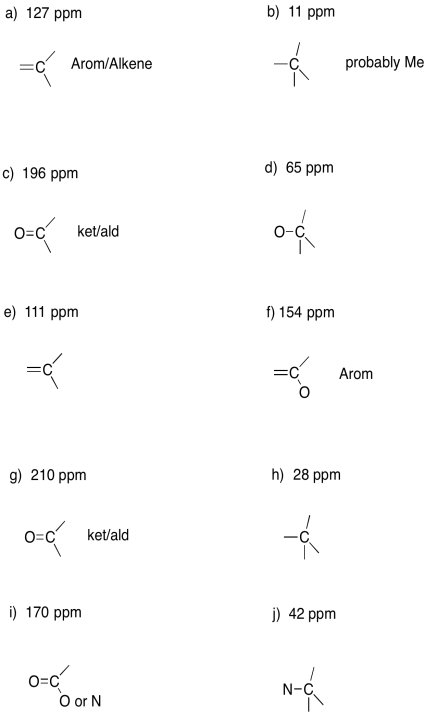
Problem NMR6.2.
a)
b)
c)

Problem NMR8.1.
a) H-Csp3
b) H-Csp3
c) H-Csp2
d) H-Csp3
e) H-Csp2
f) H-Csp2
g) H-Csp3
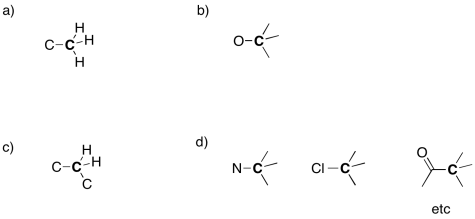
Problem NMR8.2.
a) carbon b)
carbon c) nitrogen
d) oxygen e) carbon
f) oxygen g)
nitrogen
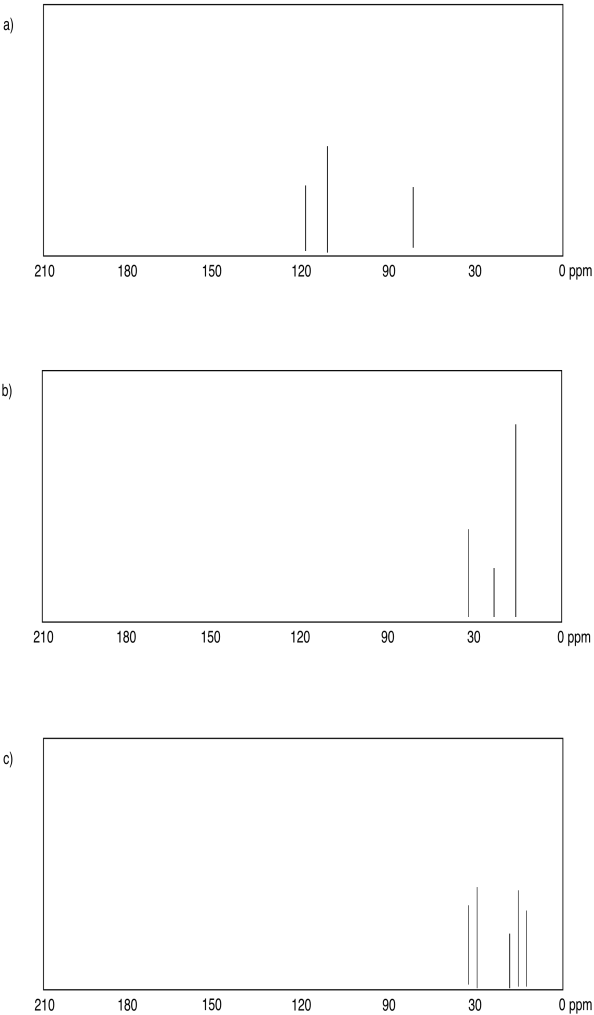
Problem NMR8.3.
a) aromatic b)
aromatic c) alkene
d) alkene e) alkene
f) aromatic
Problem NMR8.4.
a) H-CAr-C
b) H-CAr-C c) H-CAr-N
d) C=O e) C=O
f) H-CAr-N g)
H-CAr-N
Problem NMR8.5.
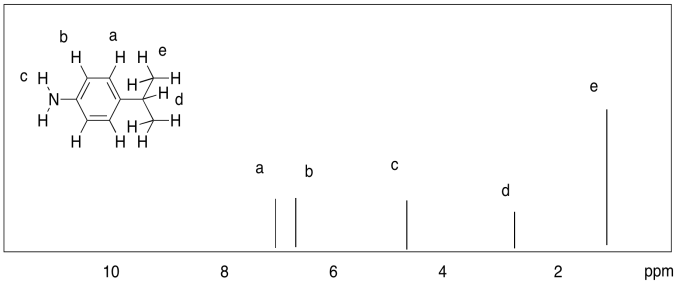
a) 3.4 ppm: Ha
1.5 ppm: Hb, Hc
0.9 ppm: Hd
b) 7.4 ppm: Hd
6.9 ppm: Hb, Hc
3.7 ppm: Ha
c) 10.1 ppm: Ha
7.9 ppm: Hb 7.6 ppm:
Hd 7.5 ppm: Hc
d) 7.9 ppm: Hb
7.6 ppm: Hd 7.4 ppm: Hc
2.5 ppm: Ha
Problem NMR8.6.
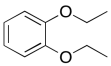
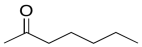
a)
b)
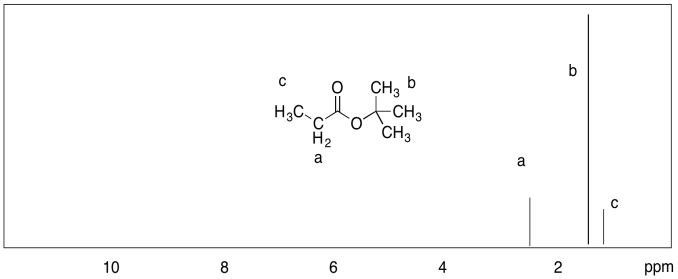
c)
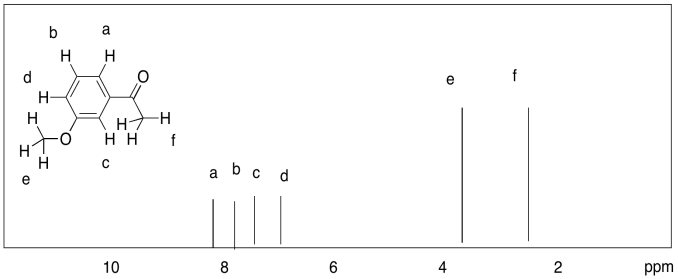
d)
Problem NMR9.1.
a) 0.9 ppm, 6H; 1.0 ppm, 6H (1:1 ratio)
b) 0.9 ppm, 6H; 1.0 ppm, 12H (1:2 ratio)
c) 0.9 ppm, 6H; 1.0 ppm, 16H (3:8 ratio)
d) 0.9 ppm, 6H; 1.0 ppm, 10H (3:5 ratio)
e) 0.9 ppm, 6H; 1.0 ppm, 8H (3:4 ratio)
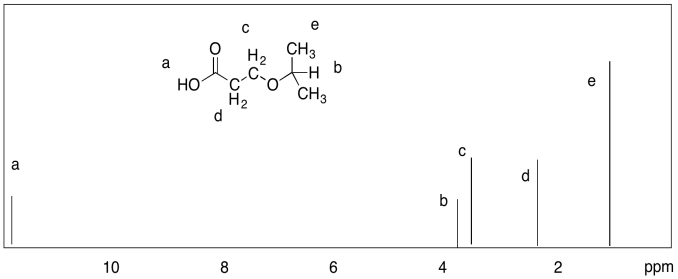
Problem NMR9.2.
a)
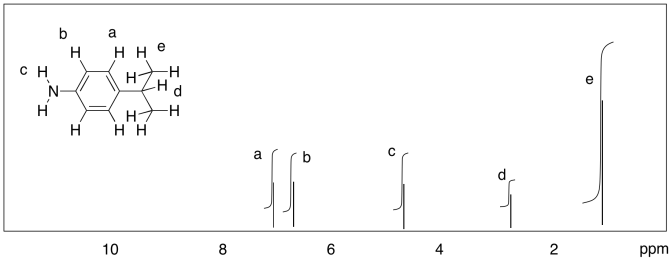
b)
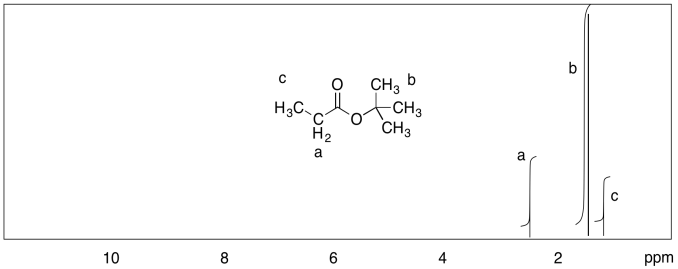
c)
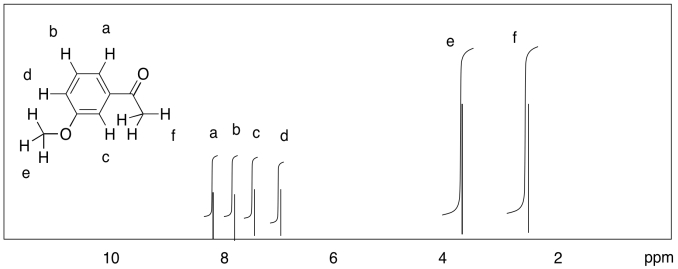
d)
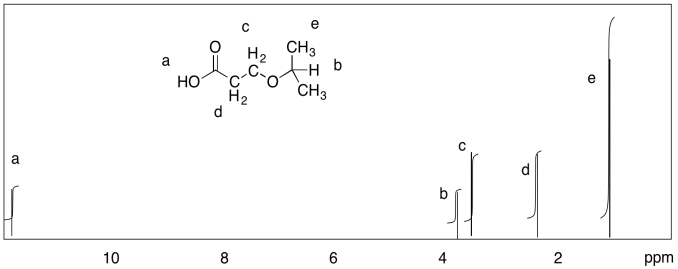
Problem NMR9.3.

Problem NMR9.4.

Problem NMR9.5.
a) 5:2:3
Problem NMR10.1.
(There will be some variation in the shift depending on
the rest of the structure; this is just an estimate.)
a) 3.5 ppm, quartet, 2H
b) 1.5 ppm, sextet, 2H c) 2.6
ppm, septet, 1H
d) 2.3 ppm, quintet, 1H
e) 2.2 ppm, quartet, 2H f)
1.7 ppm, nonet, 1H
Problem NMR10.2.
(There will be some variation in the shift depending on
the rest of the structure; this is just an estimate.)
a) 7.8 ppm, doublet, 1H
b) 8.4 ppm, singlet, 1H c) 6.7 ppm,
singlet, 1H
d) 7.2 ppm, triplet, 1H
e) 6.9 ppm, doublet, 1H
Problem NMR10.3.
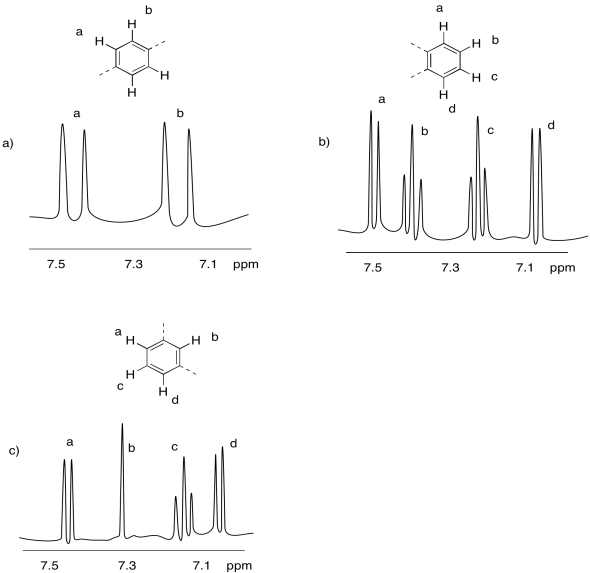
Problem NMR10.4.
3.4 ppm, doublet: CH-CH2-O
2.1 ppm, singlet: OH
1.7 ppm, nonet: (CH3)2CHCH2
0.9 ppm, doublet: CH(CH3)2
Problem NMR10.5.
a) This is a simulated spectrum. The peaks
at f, e, and c are singlets. The peak at d is a doublet. The peaks
at a & b are unfortunately coincident, so their multiplicities are obscured, but
they would be doublets & triplets, respectively.
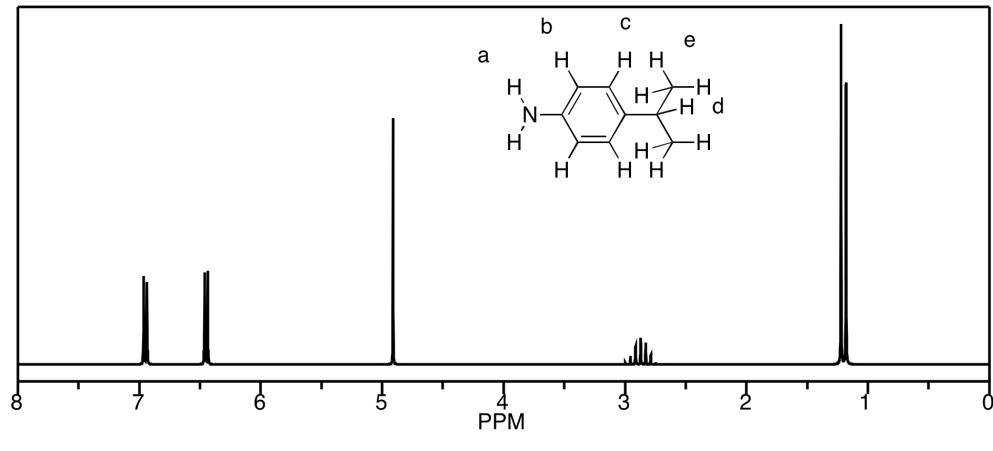
b)

c)
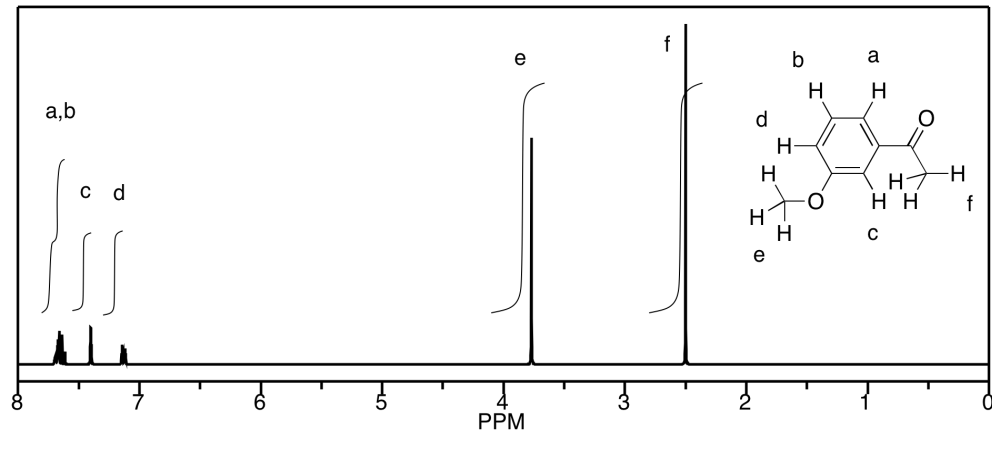
d) The peaks at b and c unfortunately coincide,
but they would be a septet and a triplet, respectively. Otherwise, a is a
singlet, d is a triplet, and e is a doublet.
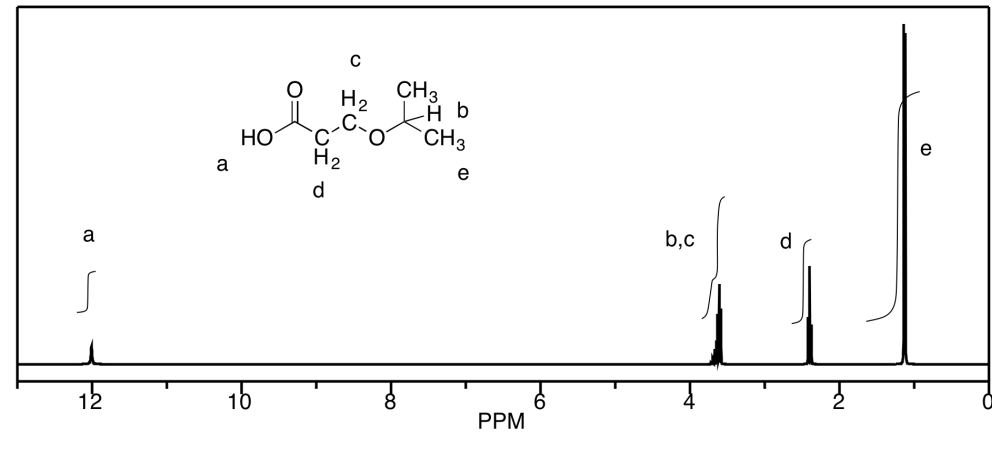
Problem NMR11.1.

Problem NMR11.2.
a) A saturated aliphatic chain would have formula
CnH2n+2. Oxygen does not affect the C:H ratio. 2(6) + 2 = 14; 14 - 10 = 4 missing
hydrogens; 4/2 = 2 units of unsaturation. Either there are two rings or two
double bonds or one of each.

Problem NMR11.3.
a) A saturated aliphatic chain would have formula
CnH2n+2. Oxygen does not affect the C:H ratio. 2(5) + 2 = 12;
12 - 8 = 4 missing
hydrogens; 4/2 = 2 units of unsaturation. Either there are two rings or two
double bonds or one of each.

Problem NMR11.4.
a) A saturated aliphatic chain would have formula
CnH2n+2. Oxygen does not affect the C:H ratio. 2(10) + 2 =
22; 22 - 12 = 10 missing
hydrogens; 10/2 = 5 units of unsaturation. Either there are five rings or five
double bonds or a combination of each, such as a ring and four double bonds.
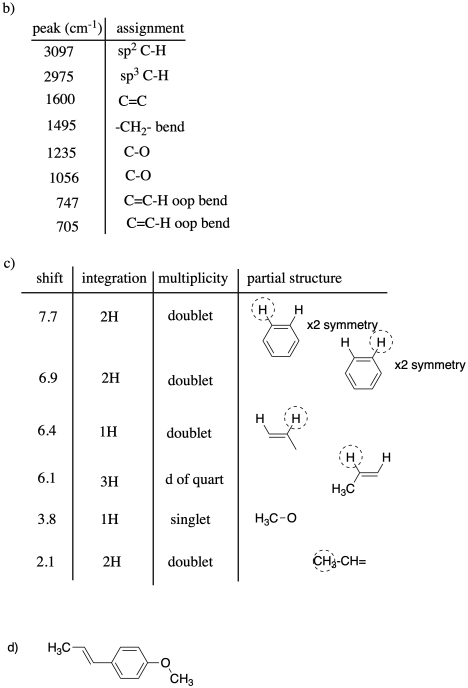
Problem NMR12a.1.
Fill in partial structures for the following peaks.
Aromatic (benzene etc) peaks are labeled "Ar" to distinguish from alkene peaks
that show up further upfield (lower shift). Also, some peaks may be in two
symmetric positions and are labeled with "x2".
a) 10.1 ppm, 1H, triplet, CH2-CH=O b) 3.4 ppm,
1H, septet, O-CH(CH3)2
c) 7.3 ppm, 2H, triplet,
CH=CH-CH x 2 (Ar) d) 5.4 ppm, 1H, quartet, CH3-CH=C
e) 1.4
ppm, 2H, sextet, CH3-CH2-CH2 f) 8.0 ppm, 1H,
singlet, C=CH-C (Ar)
g) 2.1 ppm, 3H, singlet, CH3-C=C or CH3-C=O
or CH3-N; need context to choose
h)
6.8 ppm, 2H, doublet, CH=CH-C x 2 (Ar)
i) 0.9 ppm, 6H, doublet, CH-CH3 x 2
Problem NMR12a.2.
Identify the errors in the following partial structures:
a)
3.6 ppm, 2H, triplet, CH2-CH2 the
first carbon must be attached to O to have a shift at 3.6 ppm
b) 2.1 ppm, 2H, singlet, CH3-C=C
the integral says only 2H, not 3H
c) 7.4 ppm, 2H, doublet, CH=CH2-C
the shift implies aromatic, so there can only be one H per carbon; must be
symmetry
d)
1.8 ppm, 2H, quintet, CH2-CH4
there can't be four hydrogens on one carbon; must be some hydrogens on each side
e) 7.8 ppm, 1H, triplet, -CH=CH2 the
shift implies aromatic, so there can only be one H per carbon; must be one on
each side
f) 1.7 ppm, 1H, nonet, NH2-CH(CH3)2 an attached nitrogen
would shift this hydrogen past 2 ppm; also, coupling is rarely seen across O or
N, so the two neighbouring H on the left are probably on a carbon
Problem NMR12a.3.
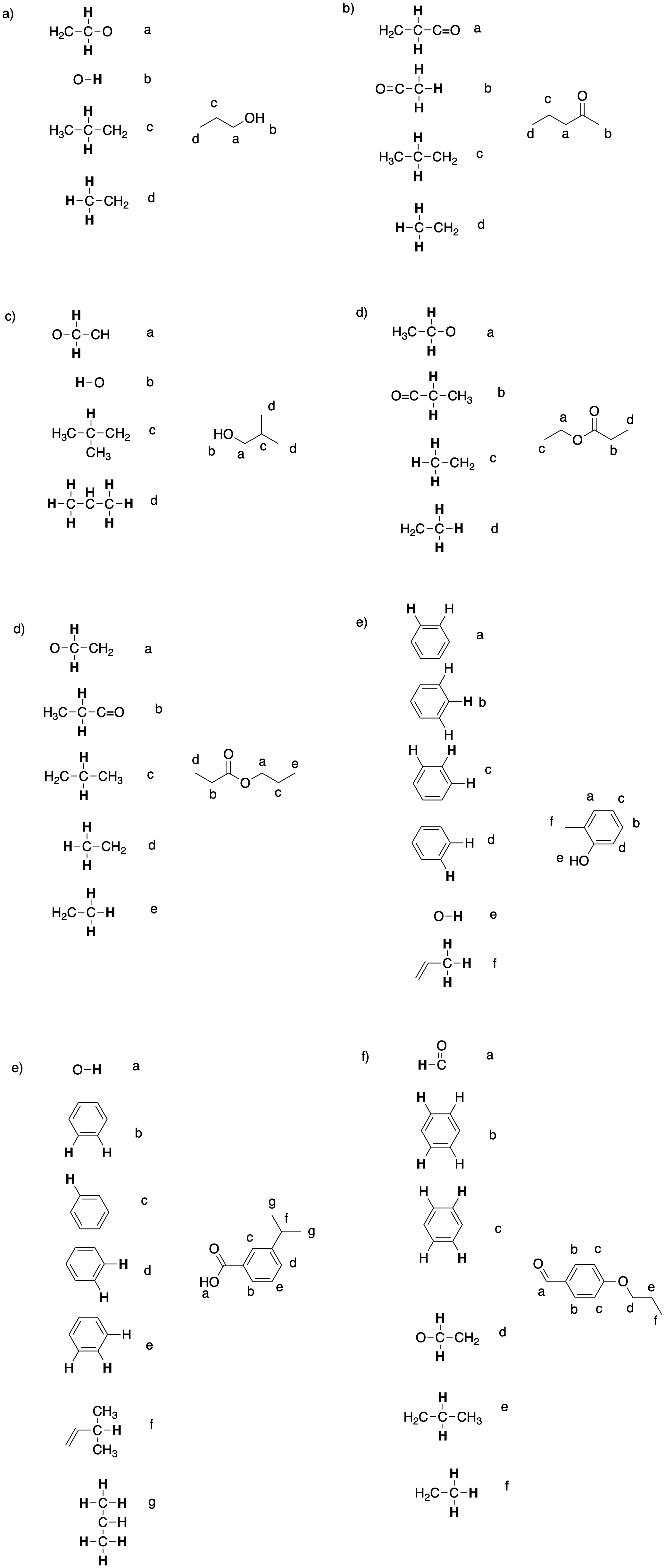
Problem NMR12.1.
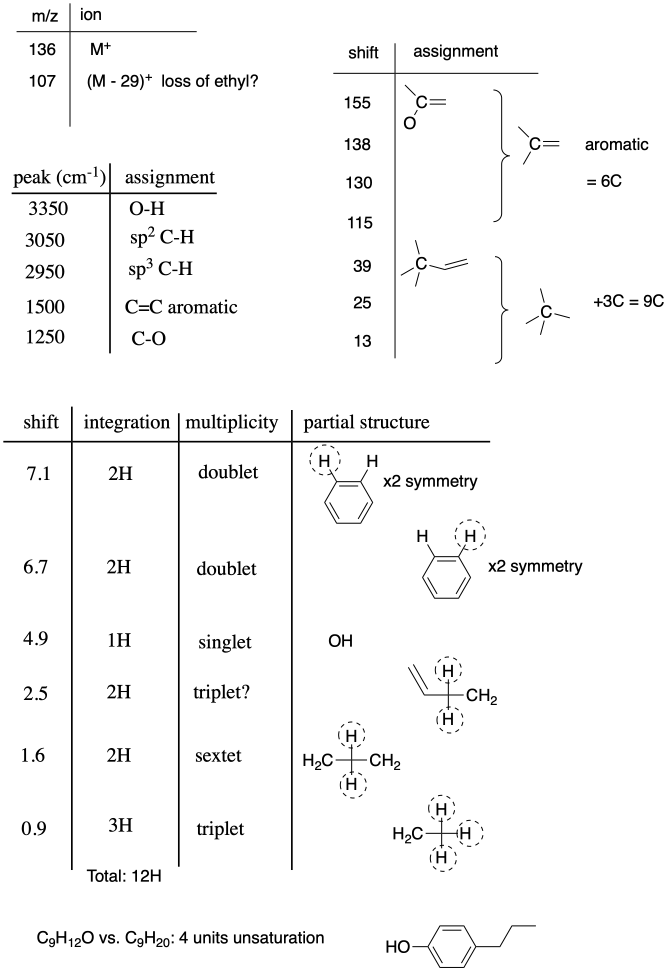
Problem NMR12.2.
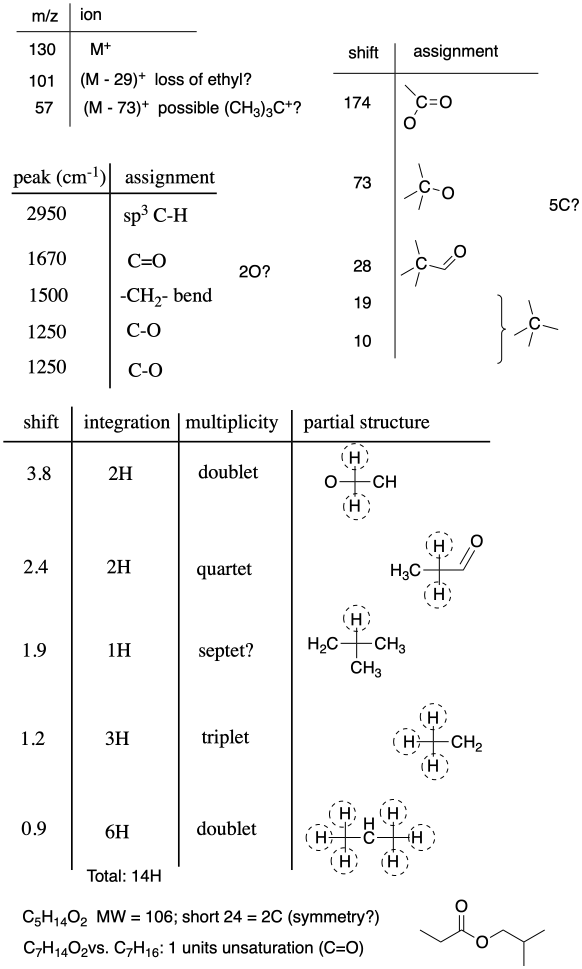
Problem NMR 13.1.
a) TBME b)
acetone c) THF
d) methanol e) ethyl acetate
Problem NMR 14.1.
a) appearance of CH-O near 3.5 ppm (multiplet, 1H)
b) appearance of CH2-O near 3.5 ppm (triplet,
2H); disappearance of =CH near 5-6 ppm (mutiplets, total 3H)
c) appearance of HC=O near 10 ppm (triplet, 1H);
disappearance of =CH near 5-6 ppm (mutiplets, total 3H)
d) appearance of HC=O near 10 ppm (triplet, 1H);
disappearance of CH2-O near 3.5 ppm (doublet, 2H)
e) appearance of CH2-O near 3.5 ppm (triplet,
2H)
f) appearance of CH2-O near 4 ppm (triplet,
2H)
g) appearance of =CH near 5-6 ppm (mutiplets, total 2H);
disappearance of HC=O near 10 ppm (triplet, 1H);
h) disappearance of =CH near 5-6 ppm (mutiplets, total
2H); appearance of triplet:sextet:triplet pattern between 1-2 ppm
i) appearance of HC=O near 10 ppm (triplet, 1H);
disappearance of CH2-O near 3.5 ppm (doublet, 2H)
j) appearance of CH-O near 3 ppm (singlet, 3H) and 3.5
ppm (sextet, 1H); disappearance of =CH near 5-6 ppm (mutiplets, total 2H)
Problem NMR15.1.
a) student 1: Let's use the H2C-O peak of
ethyl propanoate at 4 ppm and the acetonitrile methyl at 2 ppm. The ratio
appears to be 2:1, but they represent 2 protons and 3 protons, respectively.
That means the ratio of molecules is 2/2:1/3 = 3:1 ethyl propanoate :
acetonitrile.
student 2: We'll use the H2C-O peak of ethyl
propanoate at 4 ppm and the H2C-O peak of THF at 3.5 ppm. The
ratio appears to be 3:2, but they represent 2 protons and 4 protons,
respectively. That means the ratio of molecules is 3/2:2/4 = 12:4 = 3:1
ethyl propanoate : THF.
student 3: Look at the H2CCl2 peak of
dichloromethane at 5 ppm and the H2C-O peak of THF at 4 ppm. The
ratio appears to be 1:2, and they both represent 2 protons, so the ratio of molecules is
1:2 dichloromethane : ethyl propanoate.
b) student 1: The sample is [1/(1+3)]x100% = 25%
acetonitrile.
student 2: The sample is [1/(1+3)]x100% = 25% THF.
student 3: The sample is [1/(1+2)]x100% = 33%
acetonitrile.
Problem NMR15.2.
The obvious NMR handles are the H-C=O aldehyde proton at
10 ppm for benzaldehyde and the alcohol-adjacent H-C-O proton at 4.5 ppm for
1-phenylpropanol.
Each of those peaks represents one proton, so the
integral ratio of 1:2 suggests a ratio of bezaldehyde to 1-phenylpropanol of of
1:2. That translates into 33% benzaldehyde, 67% 1-phenylpropanol.
Problem NMR15.3.
The NMR handles here are the H-C=O aldehyde proton at 10
ppm for benzaldehyde and the alcohol-adjacent H2C-O protons near 5
ppm for benzyl alcohol.
In this case, we need to correct for the differing
numbers of protons represented by each peak: 1H for the aldehyde peak but 2H for
the alcohol one. The integral ratio of 1:6 therefore suggests a ratio of
bezaldehyde to 1-phenylpropanol of of 1:3. That translates into 25%
benzaldehyde, 75% 1-phenylpropanol.
Problem NMR15.4.
We could use the peak corresponding to the O-CH-C=O
proton above 5 ppm for the repeat unit and the peak for the CH2-O
proton in the initiator/end group near 3.5 ppm. The integral ratio is
24:1, but they represent different numbers of hydrogens, so the repeat unit to
end group ratio is really 24/1:1/2, or 48:1. The degree of polymerization
is 48.
Problem NMR16.1.
a) 9 unique carbons. Remember, this benzene is not symmetric.
b) 8 unique carbons.
c) 9 unique carbons. There are two identical methyl groups.
d) 5 unique carbons. There are two identical methyl groups.
Problem NMR16.3.
a) A tetrahedral or sp3 carbon attached to oxygen.
b) A trigonal planar or sp2 carbon; could be an alkene carbon or else an aromatic carbon with shielding effects (such as a nighbouring π-donor).
c) A trigonal planar or sp2 carbon in a carbonyl. Above 200 ppm is probably a ketone; aldehydes are near 200 ppm, but esters and other carboxyloids are closer to 170 or 180 ppm.
d) A tetrahedral or sp3 carbon next to a nitrogen; possibly next to a double bond (alkene C=C, aromatic C=C, or carbonyl C=O). Other groups further away could be responsible for the slight downfield shift but those possibilities become more speculative.
e) A trigonal planar or sp2 carbon; possibly in an aromatic with an attached electronegative atom such as oxygen. Alternatively, it could be part of a carbonyl but with an attached π-donor; this far upfield, it would have to be a nitrogen donor.
c) A trigonal planar or sp2 carbon in a carbonyl. Likely the C=O carbon of an esters and carboxylic acid; the neighbouring oxygen is a π-donor so it shields the carbon and moves its shift upfield.
Problem NMR16.4.
a) Approximately 120 ppm. The nitro groups have a deshielding effect but that is likely to be offset by the resonance shielding effect of the oxygen π-donor.
b) Approximately 35 ppm for a tetrahedral or sp3 carbon next to a carbonyl. In a ketone, this peak might be as far downfield as 40 ppm but the π-donating effect of the ester oxygen means this carbon will not be quite so deshielded.
c) Approximately 75 ppm. An sp3 carbon adjacent to an oxygen may be around 50-60 ppm, whereas next to a benzene it may be around 30 ppm. The effect is additive for the carbon between the benzene and the oxygen.
d) Approximately 45 ppm. An sp3 carbon adjacent to an carbonyl may be around 30-40 ppm, whereas next to an alkene it may be around 30 ppm. The effect is additive for a carbon between both groups. Note that this compound would be susceptible to tautomerism; a proton transfer would gie a more stable conjugated isomer.
Problem NMR16.5.
a) The additive effect of three electronegative chlorines shift this hydrogen far downfield. For comparison, CH2Cl2 has a peak around 5.2 ppm and CH3Cl has a peak around 3 ppm.
b) This upfield shift results from π-donation from the oxygen, which places some negative charge on the CH2 position (but not the neighbouring CH position).
c) Both the ortho- (or 1,2-) and para- (or 1,4-) positions are strongly deshielded by the nitro group, a strong π-acceptor. The meta- (or 1,3-) position is not as strongly deshielded by this resonance effect.
Problem NMR16.6.
a) This is a typical position for a hydrogen on an aromatic (benzene) ring.
b) This is a typical position for the acidic hydrogen of a carboxylic acid group. The acidity of the positions places partial positive charge on this hydrogen, deshielding it and moving it downfield.
c) This is a typical position for a hydrogen on an sp3 or tetrahedral carbon that is attached to an oxygen.
d) This is a typical position for a hydrogen on an sp2 or trigonal planar carbon that is attached to an oxygen by a double bond (C=O or carbonyl). This position is usually diagnostic of an aldehyde
e) This is a typical position for a hydrogen on an aromatic (benzene) ring with an attached electron-withdawing group. For example, a carbonyl or a nitro group ortho- or para- to this position would strongly deshield it by π-accepting resonance effects. Less commonly, pyridine hydrogens (aromatic ring containing nitrogen) can show up here because of the electronegative nitrogen in the ring. Also less commonly, phenol OH hydrogens (OH attached to benzene) can show up around 7-8 ppm because of the acidity of the proton; all other alcohol OH hydrogens show up between 1 and 5 ppm.
f) This is a position seen in hydrogens on tetrahedral or sp3 carbons attached to double bonds (alkenes and aromatics). In addition, hydrogens on tetrahedral or sp3 carbons attached to carbonyls also show up in this region.
g) This is a typical position for an alkene hydrogen.
Problem NMR16.7.
a) Close to 8 ppm. Aromatic hydrogens are typically around 7 ppm, but the resonance effect of the neighbouring ester, an electron-withdrawing group, places partial positive charge on the carbon attached to this hydrogen, deshielding it and moving its position downfield.
b) Approximately 5 ppm. A hydrogen on an sp3 (or tetrahedral) carbon next to an oxygen is often between 3-4 ppm, whereas one next to an alkene or benzene is just above 2 ppm. These effects are additive, so a set of hydrogens on a tetrahedral carbon between a benzene and an oxygen shows up near 5 ppm.
c) About 3.5 ppm. A hydrogen on an sp3 (or tetrahedral) carbon next to an oxygen is often between 3-4 ppm.
d) Around 10 ppm. This hydrogen is attached to a carbonyl carbon, resulting in both a geometry effect (sp2 carbon) and a strong electronegativity effect that move it downfield.
e) Around 6 ppm. The typical range for alkene hydrogens is 5-6 ppm, although neghboring electron-donating groups can shift them slightly upfield and electron-withdrawing groups can shift them downfield into the aromatic region.
f) A little below 7 ppm; maybe 6.8 ppm. Aromatic hydrogens are typically around 7 ppm, but the resonance effect of the neighbouring ether, an electron-donating group, places partial negative charge on the carbon attached to this hydrogen, shielding it and moving its position upfield.
g) About 2.1 ppm. A hydrogen on an sp3 (or tetrahedral) carbon next to an carbonyl is usually just above 2 ppm. If this were a ketone, the hydrogens might show up at 2.3 ppm, but the π-donor effect of the ester oxygen shields this carbonyl slightly.
h) About 2.1 ppm. A hydrogen on an sp3 (or tetrahedral) carbon next to a double bond (whether an alkene, a benzene, or a carbonyl) is usually just above 2 ppm.
Problem NMR16.8.
a) This quartet indicates 3 neighbouring hydrogens. The simplest explanation is that the hydrogen (or hydrogens) corresponding to this peak is next to a CH3 group.
b) This peak shows a case of complex coupling. If you don't know what complex coupling is, you may be better off sticking with the other examples. In this case, we see a doublet of doublets. That indicates two different neighbours with very different relationships to the hydrogen we are observing. For example, they may be at very different dihedral angles from the hydrogen we are observing; one of them could be cis- to the observed hydrogen whereas the other is trans- to it, either across a double bond or in terms of faces on an aliphatic or paraffinic (non-aromatic) ring. Note that trans-relationships lead to larger coupling constants and wider splittings.
c) This triplet indicates 2 neighbouring hydrogens. The simplest explanation is that the hydrogen (or hydrogens) corresponding to this peak is next to a CH2 group.
d) This peak shows a case of complex coupling. If you don't know what complex coupling is, you may be better off sticking with the other examples. In this case, we see a doublet of triplets. That indicates two different sets of neighbours with very different relationships to the hydrogen we are observing. For example, they may be at very different dihedral angles from the hydrogen we are observing; two of them could be cis- to the observed hydrogen whereas the other is trans- to it, in terms of faces on an aliphatic or paraffinic (non-aromatic) ring. Another common case is that one neighbour is at the other end of a C=C bond whereas the other nighbours are at the other end of a C-C bond.
e) This septet indicates 6 neighbouring hydrogens. That is too many hydrogens to be on one neighbouring carbon, which can only have 4 bonds, after all. The simplest explanation is that the hydrogen (or hydrogens) corresponding to this peak is next to two CH3 groups.
f) This peak shows a case of complex coupling. If you don't know what complex coupling is, you may be better off sticking with the other examples. In this case, we see a doublet of triplets of doublets. That indicates three different sets of neighbours with very different relationships to the hydrogen we are observing. For example, they may be at very different dihedral angles from the hydrogen we are observing. One of them could be cis- to the observed hydrogen; a second, different set of two hydrogens may also be cis to the one we are looking at; whereas the third set, just one hydrogen, is trans- to it.
Problem NMR16.10.
The para- (or 1,4-) disubstituted benzene has an axis or plane of symmetry, but the 1-end and 4-end are different from each other. That results in two unique sets of hydrogens: those nearer the nitro and those nearer the chlorine. Each hydrogen in either set has just one near neighbour (one of the hydrogens from the other set. The result is two different doublets.
The ortho- (or 1,2-) disubstituted benzene has no symmetry in this case, as it is broken by the difference between the nitro and chloride. Each hydrogen is therefor unqique. The hydrogens nearest the chlorine and the nitro each have one neighbour, so their resonances appear as doublets. The other two hydrogens each have one neighbour on either side, so their peaks appear as triplets.
The meta- (or 1,3-) disubstituted benzene has no symmetry in this case, as it is broken by the difference between the nitro and chloride. Each hydrogen is therefor unqique. The hydrogens nearest the chlorine and the nitro each have one neighbour, so their resonances appear as doublets. The single hydrogen between those two has one neighbour on either side, so its peak appears as a triplet. Finally, there is one hydrogen in between the nitro and chlorine; with no near hydrogen neighbours, the peak due to this hydrogen is a singlet.
Problem NMR16.11.
a) 2H : 1H : 1H : 3H
b) 2H : 2H : 1H : 6H
c) 2H : 1H : 2H : 1H : 3H. Note that it is sometimes difficult to integrate nearby peaks independently. The NMR software is not telling you that these shapes form just one peak; it does not have the intelligence to make that decision. Look for an inflection point (a bend in the integral line) that may tell you the integral is transitioning from one peak to the next.
This site is written and maintained by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's
University (with contributions from other authors as noted). It is freely
available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
Navigation:
Back to NMR
Back to Structure Determination
Back to Structure & Reactivity






![]()























