in Coordination Complexes and Organometallic Compounds

CC13. More Solutions to Selected Problems

Problem CC7.1.

a)  Zn(II), because it is smaller and less polarizable.

b)  K⁺, because it is less electronegative.

c)  Fe(III), because of the higher charge.

Problem CC7.2.

a)  Me₃P, because phosphorus is larger and more polarizable than nitrogen.

b)  Iodide, which is larger and more polarizable than chloride.

c)  Azide, which has a more polarizable, delocalized pi bonding system.

Problem CC7.3.

a)  ZrO₂

b)  CdS

c)  WO₃

d)  ZnS

e)  Cu₂S

Problem CC7.4.

a)  Hg(I) and Hg(II) are both large, polarizable ions.  They are soft cations and should bind well to soft donors. 

b)  The most common soft donor is a sulfur atom or sulfide ion; in amino acids, that suggests cysteine or methionine.

Problem CC7.5.

Fe(III) is a hard cation and should bind well to oxygen donors.  Enterobactin has several oxygen donors it could provide to the iron.  In fact, there is a pair of OH groups on each of the benzene rings in enterobactin.  These benzene rings with two OH groups next to each other are called "catechols".  Because there are three of these groups in enterobactin, and there is enough space in between for the groups to fold around a central atom, enterobactin is a chelating (hexadentate) donor with a high binding constant.

Problem CC8.1.

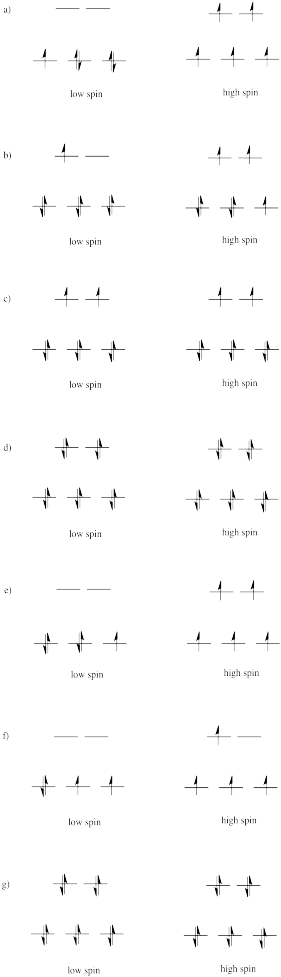
Problem CC8.2.

The three orbitals shown above interact a little more strongly with the ligands.  The three orbitals shown below interact a little more weakly.

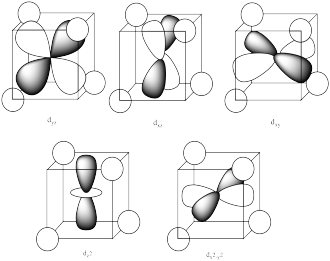
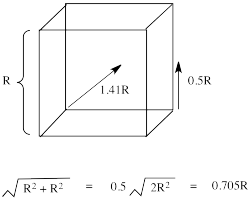
The reason for the difference in the interaction has to do with how close the nearest lobe of a d orbital comes to a ligand.  There are really two possible positions:  the face of a cube or the edge of a cube.  If the ligands are at alternating corners of the cube, then the orbitals pointing at the edges are a little closer than those pointing at the faces of the cube.

Problem CC8.3.

The ligands do not overlap with the d orbitals as well in tetrahedral complexes as they do in octahedral complexes.  Thus, there is a weaker bonding interaction in the tetrahedral case.  That means the antibonding orbital involving the d electrons is not raised as high in energy, so the splitting between the two d levels is smaller.

Problem CC8.4.

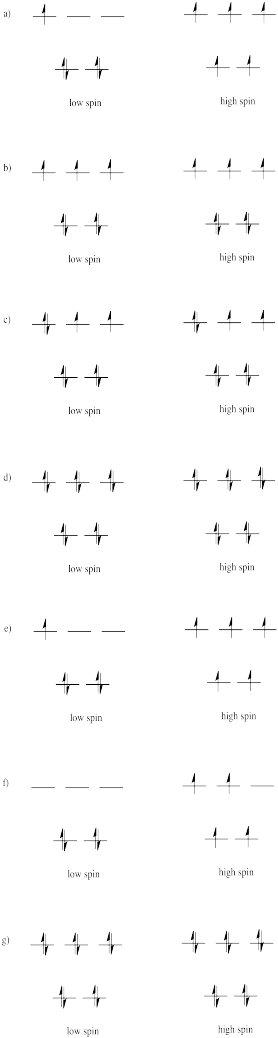
Problem CC8.5.

Because the d orbital splitting is much smaller in the tetrahedral case, it is likely that the energy required to pair two electrons in the same orbital will be grester than the energy requied to promote an electron to the next energy level.  In most cases, the complex will be high spin.

Problem CC8.6.

The orbitals are shown in order of energy.

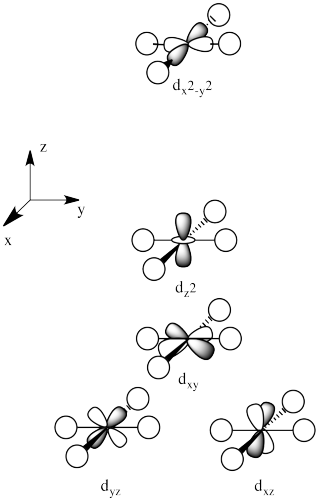
Problem CC8.7.

a. [Fe(py)₆]²⁺ 3d metal, M⁺², pi acceptor ligand → low spin

b. [Fe(H₂O)₆]²⁺ 3d metal, M⁺², pi donor ligand → high spin

c. [FeBr₆]^3- 3d metal, M⁺³, pi donor ligand → high spin

d. [Co(NH₃)₆]³⁺ 3d metal, M⁺³, sigma donor ligand → low spin

e. [Cu(NH₃)₆]²⁺ 3d metal, M⁺², sigma donor ligand → low spin

f. [Rh(CO)₆]³⁺ 4d metal, M⁺³ → low spin

g. [Cr(CO)₆]³⁺ 3d metal, M⁺³, pi acceptor ligand → low spin

f. [PtCl₆]^2- 5d metal, M⁺⁴ → low spin

Problem CC8.8.

a. [Zn(NH₃)4] ²⁺ 3d metal, d¹⁰, sigma donor ligand → tetrahedral

b. [NiCl₄] ²⁺ 3d metal, d⁸, pi donor ligand → tetrahedral

c. [Ni(CN)₄] ^2- 3d metal, d⁸, pi acceptor ligand → square planar

d. [Ir(CO)(OH)(PCy₃)₂] ²⁺ 5d metal, d⁸ → square planar

e. [Ag(dppb)₂]¹⁺ 4d metal, d¹⁰, sigma donor ligand → tetrahedral

f. [PtCl₂(NH₃)₂] 5d metal, d⁸ → square planar

g. [PdCl₂(NH₃)₂] 4d metal, d⁸, M⁺², sigma donor ligand → square planar

i. [CoCl₄] ^2� 3d metal, d⁷, sigma donor ligand → tetrahedral

f. [Rh(PPh₃)₃Cl] 5d metal,  d⁸ → square planar

Problem CC9.1.

a. Fe⁺²

d⁶ low spin
SE = [-0.4(6)+ 0.6(0)] Δo + 3PE
= [-2.4] Δo + 3PE

d⁶ high spin
SE = [-0.4(4)+ 0.6(2)] Δo + 1PE
= [-.4] Δo + 1PE


b. Co⁺²

d⁷ low spin
SE = [-0.4(6)+ 0.6(1)] Δo + 3PE
= [-1.8] Δo + 3PE

d⁷ high spin
SE = [-0.4(5)+ 0.6(2)] Δo + 2PE
= [-.8] Δo + 1PE

c. Co⁺³
d6 so this looks the same as Fe+2

d. Mn⁺²

d⁵ low spin
SE = [-0.4(5)+ 0.6(0)] Δo + 2PE
= [-2.0] Δo + 2PE

d⁵ high spin
SE = [-0.4(3)+ 0.6(2)] Δo + 0PE
= [0] Δo

e. Ti⁺³
d¹ so there is no possibility of low spin or high spin

Problem CC9.2.

a)  [Mn(OH₂)₆]²⁺: low-spin: SE = LFSE + PE = [0 - (0.4(5)]Δ_o + 2PE = (-2.0)(7,800) + 2(20,400) cm^-1 = -14,000 + 40,800 = 26,800 cm^-1

high-spin: SE = LFSE + PE = [(0.6(2) - (0.4(3)]Δ_o + 0PE = (1.2 - 1.2)(7,800) + 0(20,400) cm^-1 = (0)(7,800) + 0 cm^-1 = 0 cm^-1

so high-spin.

b)  [Fe(CN)₆]^4-: low-spin: SE = LFSE + PE = [0 - (0.4(6)]Δ_o + 3PE = (-2.4)(33,200) + 3(14,200) cm^-1 = -79, 680 + 42,600 cm^-1 = -37,080 cm^-1

high-spin: SE = LFSE + PE = [(0.6(2) - (0.4(4)]Δ_o + PE = (1.2 - 1.6)(33,200) + 14,200 cm^-1 = (- 0.4)(33,200) + 14,200 cm^-1 = -13, 280 + 14,200 = 920 cm^-1

so low-spin.

c)  [Co(NH₃)₆]³⁺: low-spin: SE = LFSE + PE = [0 - (0.4(6)]Δ_o + 3PE = (-2.4)(23,000) + 3(16,900) cm^-1 = -55,200 + 50,700 cm^-1 = -4,500 cm^-1

high-spin: SE = LFSE + PE = [(0.6(2) - (0.4(4)]Δ_o + PE = (1.2 - 1.6)(23,000) + 16,900 cm^-1 = (- 0.4)(23,000) + 16,900 cm^-1 = -9,200 + 16,900 = 7,700 cm^-1

so low-spin.

Problem CC9.3.

high-spin d⁶

octahedral

SE = [2(0.6) -4(0.4)]Δ_o + PE

SE = -0.4Δ_o + PE

tetrahedral

 SE = [3(0.4) - 3(0.6](4/9)Δ_o + PE

SE = -0.6Δ_o + PE

ΔSE = SE_oh - SE_td  =  -0.4Δ_o + PE -(-0.6Δ_o + PE) = +0.2Δ_o

This is a slight preference for tetrahedral.

low-spin d⁶

octahedral

SE = [0(0.6) -6(0.4)]Δ_o + 3PE

SE = -2.4Δ_o + 3PE

tetrahedral

 SE = [2(0.4) - 4(0.6](4/9)Δ_o + 2PE

SE = -1.6Δ_o + PE

ΔSE = SE_oh - SE_td  =  -2.4Δ_o + 3PE -(-1.6Δ_o + 2PE) = -0.8Δ_o + PE

This is a preference for octahedral, although it would be offset by the pairing energy.

Problem CC9.4.

high-spin d⁸

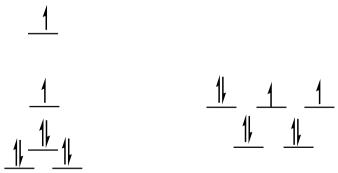
square planar

SE = [1.23 + 0.23 - 2(0.43) -4(0.51)]Δ_o + 3PE

SE = -1.44Δ_o + 3PE

tetrahedral

 SE = [4(0.4) - 4(0.6](4/9)Δ_o + 3PE

SE = -0.36Δ_o + 3PE

ΔSE = SE_sq - SE_td  =  -1.44Δ_o + 3PE -(-0.36Δ_o + 3PE) = -1.08Δ_o

This is an appreciable preference for square planar.

low-spin d⁸

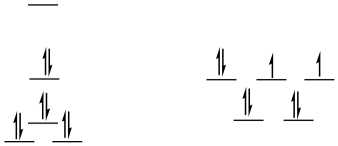
square planar

SE = [0 + 2(0.23) - 2(0.43) -4(0.51)]Δ_o + 4PE

SE = -2.44Δ_o + 4PE

tetrahedral = same as before (ls = hs for d⁸ tetrahedral)

ΔSE = SE_sq - SE_td  = -2.44Δ_o + 3PE -(-0.36Δ_o + 3PE) = -2.08Δ_o + PE

This is an even more appreciable preference for square planar, although it is offset by pairing energy.  Pairing energy would have to be twice as big as Δ_o in order to completely offet the LFSE.

Problem CC10.1.

The weaker donors include halides and oxygen donors.  Nitrogen atom donors are mostly a little stronger than that.  The strongest donors include carbon donors, especially with pi bonds.

Problem CC10.2.

Problem CC10.3.

Pi donation raises the t₂g electrons (the d electrons of proper symmetry for pi overlap with the ligands in an octahedral geometry).

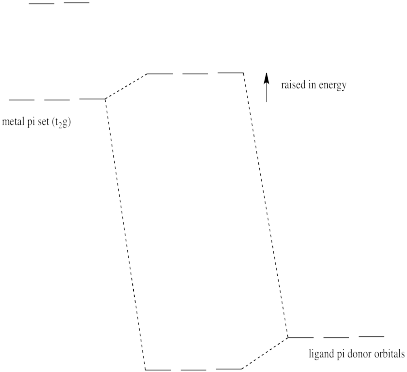
Problem CC10.6.

Because chloride is a weaker ligand than hydroxide, the d orbital splitting gets smaller.  A d-d transition would involve less energy, so it would move to longer wavelength (red shift).  

Problem CC10.7.

a) The [Cu(OH₂)₆]²⁺ ion appears blue-green, so it absorbs a reddish orange, about 650 nm; whereas the [Cu(NH₃)₂(OH₂)₄]²⁺ ion appears indigo-violet, so it absorbs yellow, about 600 nm.

b) Shorter wavelength is higher energy, according to the Planck-Einstein relation: E = hc/λ (in which h = Planck's constant, c = speed of light, λ = wavelength of photon).  The [Cu(NH₃)₂(OH₂)₄]²⁺ ion absorbs the shorter wavelength, higher energy photon.

c)  The [Cu(NH₃)₂(OH₂)₄]²⁺ ion has the greater d-d gap.

d)  The ammonia must be a stronger field ligand than water.  In general terms we might think of that as a result of ammonia being only a sigma-donor, whereas water is also a pi-donor.

Problem CC10.8.

a) The [Cu(NH₃)₆]³⁺ ion appears yellow, so it absorbs violet, about 400 nm; whereas the [Cu(NH₃)₅Cl]²⁺ ion appears pink, so it absorbs green, about 550 nm.

b) Shorter wavelength is higher energy, according to the Planck-Einstein relation: E = hc/λ (in which h = Planck's constant, c = speed of light, λ = wavelength of photon).  The  [Cu(NH₃)₆]³⁺ ion absorbs the shorter wavelength, higher energy photon.

c)  The  [Cu(NH₃)₆]³⁺  ion has the greater d-d gap.

d)  The ammonia must be a stronger field ligand than chloride.  In general terms we might think of that as a result of ammonia being only a sigma-donor, whereas chloride is also a pi-donor.

Problem CC10.9.

The green compound absorbs red; the violet compound absorbs yellow; the yellow compound absorbs violet.

 In terms of energy these absorbances can be ranked:

 (high energy) violet photon > yellow photon > red photon (low energy)

or in terms of d-d gap:

 large gap > middle gap > small gap

In the spectrochemical series, we would expect the order of corresponding ligands to be:

^-CN > H₂O > F^-

The cyano compound absorbs violet and appears yellow; the aquo compound absorbs yellow and appears violet; the fluoro compound absords red and appears green.

Problem CC10.10.

a) The [V(OH₂)₆]³⁺ ion appears yellow, so it absorbs violet, about 400 nm; whereas the [V(OH₂)₆]²⁺ ion appears pink, so it absorbs green, about 550 nm.

b) Shorter wavelength is higher energy, according to the Planck-Einstein relation: E = hc/λ (in which h = Planck's constant, c = speed of light, λ = wavelength of photon).  The   [V(OH₂)₆]³⁺ ion absorbs the shorter wavelength, higher energy photon.

c)  The   [V(OH₂)₆]³⁺  ion has the greater d-d gap.

d)  One ion contains V³⁺, whereas the other ion contains V²⁺.  As charge increases on an ion, electrons contract toward the nucleus.  However, low-lying electrons, which are closer to the nucleus to begin with, are attracted even more than are high-lying electrons.  thus, as charge increases on the ion, the d-d splitting increases.

Problem CC10.11.

Problem CC11.1.

a)  The ions in LiF are both smaller than in KBr, so the force of attraction between the ions in LiF  is greater because of the smaller separation between the charges.

b)  Calcium has a 2+ charge in CaCl₂, whereas potassium has only a + charge, so the chloride ions are more strongly attracted to the calcium than to the potassium.

Problem CC11.3.

a) labile (electrons in higher energy d orbital set)

b) not labile (all electrons in lower energy d orbitals)

c)  not labile (all electrons in lower energy d orbitals)

d)  labile (electrons in higher energy d orbital set)

e)  labile (electrons in higher energy d orbital set)

Problem CC12.1.

a) yes; ls d⁷ is eg¹, so one level has one electron and the other has none - net decrease in energy upon distortion

b) no; d⁸ is eg², so both levels have one electron -- no net change in energy upon distortion

Problem CC12.2.

a) Co²⁺ yes; d⁷ so e_g¹

b) Ag²⁺ yes; d⁹ so e_g³

c)  Ni²⁺ no; d⁸ so e_g²

d) Mn²⁺ no if hs; d⁵ so e_g².  However, if it were low-spin (unlikely with a first-row metal in a moderately low oxidation state and π-donors), then there would be degeneracy and distortion.

e) Ag⁺ no; d¹⁰ so e_g⁴

Problem CC12.3.

This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages.  It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. 

Send corrections to cschaller@csbsju.edu

This material is based upon work supported by the National Science Foundation under Grant No. 1043566.

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Navigation:

Back to Coordination Chemistry Index

Back to Reactivity

Back to Web Materials on Structure & Reactivity in Chemistry