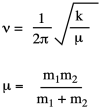
Reactivity in Chemistry
Reaction Kinetics
MK13. Kinetic Isotope Effects
The fact that atoms occur in naturally-occuring isotopes, having the same general proerties but slightly different masses, presents a useful tool for mechanistic inquiry. Different isotopomers -- that is, identical compounds containing different isotopes -- react at diffeerent rates. Most of the time, these rate differences are very small, maybe a few percent, but in some cases one isotopomer may react several times more slowly than another.
These differences in mass between two isotopomers can be detected in a number of ways, such as mass spectrometry or infrared spectroscopy. In mass spectrometry, the two isotopomers simply show up at different values of m/z because of differences in momentum between isotopomers in motion. In infrared spectroscopy, heavier isotopes are always observed at lower wavenumber than lighter isotopes. For example, a typical C-H stretching vibration is observed around 3,000 cm-1, whereas a corresponding C-D stretch shows up around 2,250 cm-1. Remember, D is a common symbol for a heavier isotope of hydrogen, 2H.
Why the difference? The classical treatment of bond vibrations observed in IR spectroscopy is rooted in Hooke's Law. This is not new science; Hooke was a 17th-century contemporary of Isaac Newton. The idea is that if you have two atoms at either end of a bond and their positions are not rigidly fixed, they can vibrate a little bit. In other words, they can stretch a little farther apart or squeeze a little closer together, at least temporarily. If the atoms get too close together, there are forces that drive them back apart; often these forces are decribed as repulsion between the nuclei, but there is also a significant kinetic energy term arising from increasing localization of the bonding electrons. If the atoms get too far apart, similarly, there is a force that snaps them back together.
Those ideas are based in quantum mechanics, but the 17th-century part comes from realizing that this bond is a little like a spring with weights at either end, and Hooke's Law is all about springs. The frequency of vibration of two weights on a spring depends on only two things: the strength of the spring and the mass of the two weights. In the context of IR spectroscopy, Hooke's Law is often presented as:
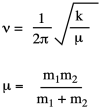
Here, k is the force constant, essentially analogous to the bond strength. We expect k to be greater for a C=O bond than a C-O bond, for example. But for two isotopomers, if we are looking at a C-H and a C-D bond, the two values of k would be essentially the same. In contrast, the value of μ (mu), the reduced mass, would vary because it depends on the mass of the two atoms at the ends of the bond, which is precisely the thing that changes between isotopes.
Problem MK13.1.
Calculate μ in the following cases:
a) a 12C-1H bond vs. a 12C-2H bond
b) a 12C-1H bond vs. a 13C-1H bond
c) a 35Cl-35Cl bond vs. a 35Cl-37Cl bond
In infrared and other vibrational spectroscopies (such as Raman spectroscopy), the spectrum shows peaks corresponding to energy differences betwen vibrational states of the molecule. When we see a C=O stretch in the IR spectrum at 1700 cm-1, we are observing the energy difference between the lowest vibrational energy level of the C=O bond and the next-lowest; we are observing the transition from the zeroth to the first excited vibrational energy level when a photon of energy corresponding to 1700 cm-1 is absorbed. If you looks very closely, you may see a small peak -- the same shape as the C=O peak at 1700 -- showing up around 3200 cm-1. This little peak is a vibrational overtone. It occurs when another photon is absorbed with energy sufficient to promote the molecule from the zeroth to the second vibrational energy level. In principle, we could observe a series of these overtones corresponding to promotion to the third, fourth, fifth vibrational levels and so on, only those peaks would become smaller and smaller and they would soon disappear off the edge of the IR spectrum.
The diagram below is called a "Morse curve" or a "Morse potential diagram". It shows the change in energy of a bond as it gets shorter or longer. At the zeroth energy level, the bond has some lassitude to lengthen and shorten. At the first excited vibrational level, it can get a little bit shorter and a little bit longer. At the second excited vibrational level, it can get a little bit longer, and so on.

Figure MK13.1. Vibrational energy levels.
At some point, we have to wonder, how long can the bond get before it isn't even a bond anymore? Conceptually, at some point, as we excite the bond one level at a time, it will eventually reach a vibrational level that allows it to break completely. We can look at that Morse curve and imagine it is showing us one side of a reaction progress diagram. At the top of the Morse curve, where the bond breaks, we have reached the transition state. After that, we slide down the other side to form an intermediate or a product.
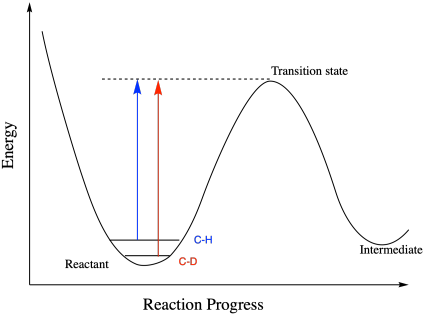
Figure MK13.2. The slightly lower vibational energy of a C-D bond results in a greater energy needed to reach the transition state than for a C-H bond.
Now we are ready to crack open kinetic isotope effects, in which two isotopomers react at different rates. Consider a C-H and a C-D bond, which are meant to break over the course of a reaction. To get either one to break, we have to get it to the top of the Morse curve. But where do they start out? At the bottom, of course, but it isn't the same bottom. Because the C-D bond has a greater reduced mass than the C-H bond, according to Hooke's Law the C-D bond has a lower vibrational frequency than the C-H bond. We all know the relationship between frequency and energy, right? They're directly proportional. That means the C-H bond is at higher energy than the C-D bond to begin with. In order to get to the transition state, the C-D bond has to travel a little bit farther in terms of energy. The C-D bond will be a little bit harder to break.
Does it really make a difference? It depends on the reaction. In the base-induced elimination of HX (or DX) from a phenethyl halide, which we expect to proceed through an E2 mechanism, it's pretty significant, as shown by work by Frank Bordwell (Columbia University) and others in the mid-twentieth century. The C-H (C-D) bond is clearly breaking as the molecule enters the transition state, and the kinetic isotope effect, kH/kD, which is the ratio of the rate of the proteo compound compared to the deutero compound, is between 5 and 7.
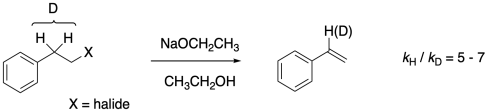
Figure MK13.3. An example of the kinetic isotope effect.
This type of case, in which an isotopic substitution probes the bond that is directly broken during the reaction, is called a primary kinetic isotope effect. Primary isotope effects are generally the largest such effects that we observe. A primary C-H isotope effect between protium and deuterium normally reaches a maximum value of approximately 7, although higher disparities have sometimes been reported for special cases such as quantum tunneling. Primary isotope effects are also quite sensitive to geometry, with larger values arising when the transfer of a hydrogen occurs in a linear fashion and much smaller values when the geometry of the interaction is nonlinear.
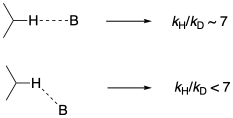
Figure MK13.4. The angle of approach can have a subtle effect on the isotope effect.
Problem MK13.2.
Primary isotope effects involving C-H bonds are relatively large. "Heavy" isotope effects, involving atoms heavier than hydrogen such as oxygen or nitrogen, are generally much smaller. Explain why.
Problem MK13.3.
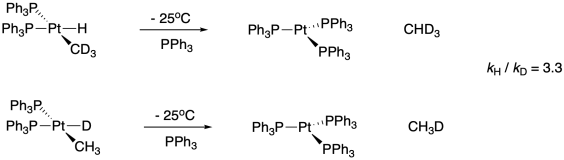
Jack Halpern's lab at University of Chicago reported the kinetic isotope effect for the reductive elimination of methane from a platinum complex. Explain the value of this isotope effect.
However, there are other, more subtle effects that can also be very important. In a secondary isotope effect, we make an isotopic substitution in the molecule, but not at the bond that is being broken. In the case above, for example, maybe we replace deuteria for the hydrogens on the carbon bearing the halide, just to see what happens.
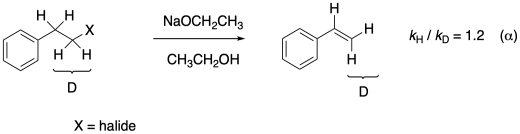
Figure MK13.5. An example of a secondary kinetic isotope effect.
It still makes a difference, even though the C-H (or C-D) bond isn't actually broken. The compound that simply contains a bystander protium reacts about 20% more quickly than the compound that contains bystander deuterium. (These numbers, by the way, are loosely based on work by A.J. Parker (Australian National University) and others in the 1960's and 1970's.) Why?
Secondary isotope effects are much more subtle and a little more complicated than primary ones. The reason for the rate difference comes from what is happening to that bystander atom as it travels from the reactant side of the reaction to the transition state. It has to do with whether that atom is in a "more tightly-held" or a "less-tightly held" position. The (mathematically-based) argument is made that in a more tightly-held position, the Morse curve describing the bond is much narrower. The rules of quantum mechanics then dictate that the vibrational levels are spaced apart at greater energy differences than they would be in a less tightly-held position, where the force constant is weaker and the Morse curve is narrower. The distinction is related to the concept of a "particle in a box", a fundamental quantum mechanical idea that says allowed energy levels in a constricted space are related by integer multiples of the lowest possible frequency of the particle. The first excited vibrational level is at an energy corresponding to double the frequency of the ground level, and so on. In any case, the wider the well, the more closely spaced the energy levels.

Figure MK13.6. The spacing between vibrational energy levels depends on the relationship between bond length and energy.
As a consequence, the difference between the C-D and C-H vibrational level is also smaller in a less-tightly held position and greater in a more-tightly held position. As a result, subtle changes in the bonding to an atom that isn't actually being broken can influence the energy needed to reach the transition state. In the example below, the difference between C-H and C-D vibrational levels gets a little smaller in the transition state than it was in the reactant, and so the reaction involving the deuterium takes a little more energy even though the C-D bond isn't being broken..
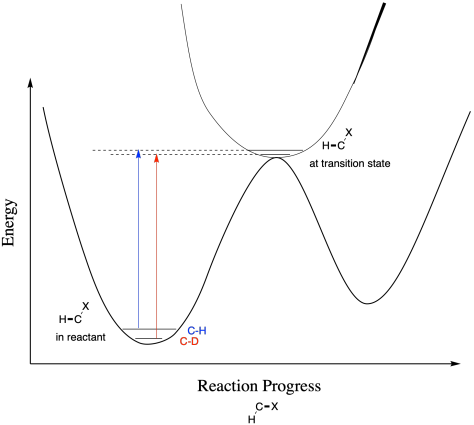
Figure MK13.7. In a secondary kinetic isotope effect, the bond is not broken at the transition state, so there is a more complicated outcome.
A secondary isotope effect is also seen when the hydrogen on the next carbon is substituted by a deuterium. These two secondary effects are called α and β secondary isotope effects based on their position relative to the leaving group.

Figure MK13.8. An example of a β secondary kinetic isotope effect.
What happens when the mechanism shifts? In this case, what happens when the mechanism changes from E2 to E1? The distinction depends very much on base strength, so in a solvolysis reaction, where the solvent is the only base present, the same reactant would be expected to undergo an E1 reaction. The secondary isotope effect indicates the deuterated molecule reacts about 30% more slowly than the proteo molecule. Secondary isotope effects are clearly pretty sensitive to the mechanistic pathway.
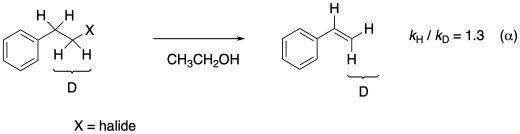
Figure MK13.8. An example of a α secondary kinetic isotope effect.
So far, all of the deuterium-containing molecules have reacted more slowly than the all-proteo molecules. That doesn't necessarily have to be the case. In a secondary isotope effect, we looked at an argument about moving to a less tightly held position in the transition state, but what if the opposite happens? What is a C-H bond moves to a more tightly held position in the transition state? In that case, the gap between the C-H and C-D energy levels should increas, and the C-D isotopomer actually has a lower activation energy than the C-H isotopomer. The deuterated molecule would react more quickly. The ratio of kH/kD would be less than one. In this case, we would have something called an "inverse isotope effect". Inverse isotope effects are also possible in primary isotope effects if the bond involving the isotope in question is becoming stronger in the transition state.
We wouldn't necessarily be able to predict whether we should expect a regular or inverse kinetic isotope effect without some knowledge of the transition state. That information might come from computational chemistry studies.
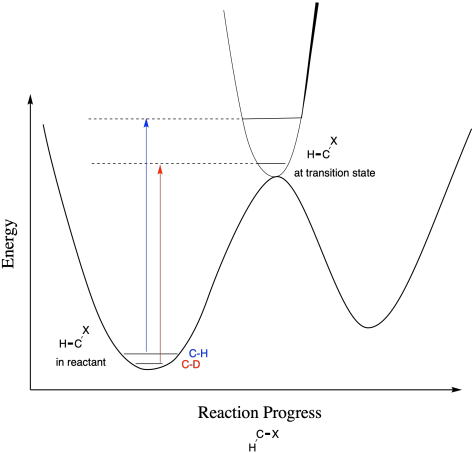
Figure MK13.9. Another complicated situation leading to an inverse secondary kinetic isotope effect.
In addition, all of the cases we have looked at so far have resulted from changes heading into the transition state, but equilibrium isotope effects are also a documented phenomenon. These isotope effects result from the difference in energy between the reactant and the product or intermediate.
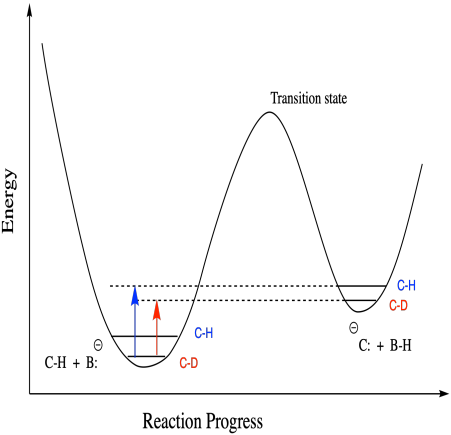
Figure MK13.10. The origin of an equilibrium kinetic isotope effect.
It's interesting to note that much of our understanding of kinetic isotope effects comes from collaborative work between Maria Goeppert Mayer and Jacob Bigeleisen during WWII's Manhattan Project. Bigeleisen later taught at University of Rochester and Stony Brook. Goeppert Mayer was paid to teach and do research at University of California, San Diego, where she was employed when she was awarded the Nobel Prize for nuclear physics, although several other institutions had graciously allowed her to work for free prior to that appointment.
This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages. It is freely available for educational use.

Structure & Reactivity in Organic,
Biological and Inorganic Chemistry by
Chris Schaller
is licensed under a
Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
This material is based upon work supported by the National Science Foundation under Grant No. 1043566.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Navigation: