MK4. Elementary Reactions and the Rate Law

How can you confirm a particular rate law through experiment?

The rate law is just the mathematical expression that shows how the rate of production of the product varies with concentrations of reactants.

Rate = d[P]/dt = k[R]^x

In other words, the rate of the reaction can be defined as the change in product concentration over changing time.  It is proportional to some rate constant, k,  as well as some reactant concentrations.  The relationship may not be linear, so the exponent x indicates that the rate will vary with reactant concentrations to some power; x might be a whole number or it might be a fraction.

If all we know is the overall equation for the reaction (these reactants are converted into those products), it is difficult to tell what the rate law will be.  The rate law will depend on the series of steps that occur to transform the reactant into product.  However, if we think we know what those individual steps are, we can use that knowledge to make educated guesses about what the rate law will look like.  In other words, knowing the mechanism of the reaction allows us to predict the rate law.  Conversely, knowing the rate law for the reaction can help us to determine the mechanism.

Consider the simplest reaction of all: one that occurs in only one step.  A is transformed into B.

A -->  B

The most common examples of these kinds of reactions are in nuclear chemistry.  Elements occur in a number of isotopes, some of which are less stable than others.  Unstable atoms tend to spontaneously decay.  A mother atom turns into a daughter atom.  They don't do it all at once, but according to a sort of clock: a certain fraction of the nuclei will decay in a certain period of time.  That same fraction of the remaining nuclei will decay in the next period of time, and so on.  That fraction per unit time corresponds to the rate constant of the reaction.

Of course, if it is always a certain fraction of atoms decaying per unit time, then the more atoms we have the more quickly we will be producing daughter atoms.  The rate of production of daughter atoms depends on the amount of mother atoms.  Consequently, the rate depends both on the concentration of mother atoms and the rate constant.

Rate = d[B]/dt = k[A]

Rate = d[daughter atom]/dt = k[mother atom]

Now let's look at another, relatively simple reaction.  Consider an aliphatic nucleophilic substitution reaction.  The kind we will think about involves the direct displacement of a leaving group by a nucleophile.  The two molecules come together and, in one step, form the products.

A + B -->   C + D

Now, this reaction will also depend on a rate constant.  At a given temperature, over a given period of time, a specific fraction of these molecules will have enough energy to undergo reaction and they will collide in the proper orientation for the substitution to take place.

What happens if the concentration of available nucleophile is doubled?  The electrophile is twice as likely to collide with a nucleophile.  What happens if the concentration of electrophile is doubled?  The nucleophile is twice as likely to collide with the electrophile.  The rate varies linearly with the concentration of both the electrophile and nucleophile.

Rate = d[C]/dt = k[A][B]

For example, in the substitution of bromomethane with sodium methylsulfide to make dimethyl thioether,

NaSCH₃ + CH₃Br    -->    CH₃SCH₃ +  NaBr

In the most likely reaction pathway, the reaction happens all in one step: reactants come together to produce the products.  The rate law is:

Rate = d[CH₃SCH₃]/dt = k[NaSCH₃][CH₃Br]

Those two scenarios form the building blocks of rate laws.  An elementary step may involve one molecule or intermediate undergoing a change by itself.  The rate of that step will depend on the concentration of the intermediate and the rate constant of the process.  Alternatively, an elementary step may involve a collision between two species.  The rate of that step will depend on the concentration of both species and the rate constant for the reaction.

• unimolecular steps depend on the concentration of one species only

• bimolecular steps depend on the concentration of two species

Multi-Step Reactions and the Steady State Approximation

If we look at another reaction, very similar to the last one, we will see a slightly more complicated case.  In cases of more sterically crowded alkyl halides, substitution reactions can take place via initial ionization, especially if the resulting carbocation is relatively stable.

For example, in the following reaction:¹

Ph₃CCl   +  NaN₃      -->      Ph₃CN₃   +   NaCl

initial ionization appears to give rise to a cationic intermediate.

Ph₃CCl   =    Ph₃C⁺   +  Cl^-       (equation 1)

Here, the equals sign suggests an equilibrium case.

Subsequently, the azide ion combines with the triphenylmethyl cation (sometimes nicknamed "trityl" cation):

Ph₃C⁺   +   N₃^-   -->   Ph₃CN₃      (equation 2)

If we think about the rate of reaction in terms of the rate of product formation, then we are looking at a simple elementary step.  Azide and trityl cation come together to make the product.

Rate = d[Ph₃CN₃]/dt = k₂[Ph₃C⁺][N₃^-]

Because sodium azide is an ionic compound, the azide concentration is equal to the dissolved concentration of sodium azide.  We know what the azide concentration is because we know how much sodium azide we dissolved.

What about the trityl cation?  What is its concentration?  The thing about reactive intermediates such as cations is that they often exist so fleetingly that we don't directly observe them.  It's not like the sodium azide, which we weigh out on a balance and add to the reaction flask.  We don't really know how much of the trityl cation is in the flask at a given time.

We do know where the trityl cation comes from.  We can use that knowledge to work out what its concentration should be.  The trityl cation comes from the trityl chloride, and that would be measured on a balance and added to the reaction mixture.

That tells us how quickly trityl cation could be produced.

Rate = d[Ph₃C⁺]/dt = k₁[Ph₃CCl],

if k₁ is the elementary rate constant for the forward equilibrium step in equation 1.

We also know that the trityl cation is a reactive intermediate, so it is probably converted into products as soon as it is formed.  Either that, or it collapses back to the trityl chloride from which it came in the first place.  We can look at that rate of consumption.  That will depend on the elementary steps that use up the cation:

Rate = -d[Ph₃C⁺]/dt = k_-1[Ph₃C⁺][Cl] + k₂ [Ph₃C⁺][N₃^-]   

 if k_-1 is the reverse step in the initial equilibrium

If the reactive intermediate is consumed as soon as it is produced, then the rate of formation equals the rate of consumption.

d[Ph₃C⁺]/dt = -d[Ph₃C⁺]/dt

or

 k₁[Ph₃CCl] =  k_-1[Ph₃C⁺][Cl^-] + k₂ [Ph₃C⁺][N₃^-]

The right hand side has some common terms.

 k₁[Ph₃CCl] =  [Ph₃C⁺] (k_-1[Cl^-] + k₂[N₃^-])

We can isolate the trityl cation concentration.

 [Ph₃C⁺]  =  k₁[Ph₃CCl]  / (k_-1[Cl^-] + k₂[N₃^-])

That means we can express that unknown concentration in terms of other quantities, and we may be able to use that to simplify things.

We already knew the rate law for product formation:

Rate = d[Ph₃CN₃]/dt = k₂[Ph₃C⁺][N₃^-]

But now we can replace that unknown quantity:

Rate = d[Ph₃CN₃]/dt =  k₁ k₂ [Ph₃CCl] [N₃^-] / (k_-1[Cl^-] + k₂[N₃^-])

So the steady state approximation, the assumption that a reactive intermediate is consumed as soon as it is formed, leads to a rate law that is independent of that unknown intermediate concentration.  That may not make you very happy, because the rate law looks a little complicated.  That's normal.  The key part now is looking at specific cases in which the rate law may simplify, and thinking about what that simplification tells us.

Looking at Limiting Cases

This rate law would be pretty straightforward if it were not for that denominator.  The denominator has two additive terms, and that makes analysis complicated.  It would be more straightforward if we did not have two things adding together.

The question we need to ask now is whether there are situations in which one of those additive terms can be ignored?  In general, that's true if one of the terms is a whole lot bigger than the other.  There are some different situations in which that could occur.  Maybe the chloride concentration is much, much smaller than the azide concentration, so small that those two terms added together are not much different from the second term alone:

i.e. if k_-1[Cl^-] + k₂[N₃^-] =  k₂[N₃^-], approximately

In that case, the rate law simplifies to a form that is easier to use:

Rate = d[Ph₃CN₃]/dt =  k₁ k₂ [Ph₃CCl] [N₃^-] / k₂[N₃^-]

or Rate = d[Ph₃CN₃]/dt =  k₁  [Ph₃CCl]

So there may be some reaction conditions under which the rate law becomes much simpler.

For the purposes of thinking about mechanism, it can also be useful to think about cases in which those elementary rate constants are very large or very small.  For example, suppose k_-1 >> k₂.

In that case,

Rate = d[Ph₃CN₃]/dt =  k₁ k₂ [Ph₃CCl] [N₃^-] / (k_-1[Cl^-] + k₂[N₃^-]) = k₁ k₂ [Ph₃CCl] [N₃^-] / k_-1[Cl^-]

That suggests a bimolecular reaction, but one that is inhibited by the leaving group.

On the other hand, suppose k₂ >> k_-1.  In that case,

Rate = d[Ph₃CN₃]/dt =  k₁ k₂ [Ph₃CCl] [N₃^-] / (k_-1[Cl^-] + k₂[N₃^-]) = k₁ k₂ [Ph₃CCl] [N₃^-] / k₂[N₃^-]

Or

Rate = k₁  [Ph₃CCl]

And that is what we think of as a first order rate law for an S_N1 reaction.  In other words, in that kind of reaction, the step in which the cation and anion combine is rapid compared to the initial equilibrium for ion formation.

Problem MK4.1.

The Bergman lab (Berkeley) discovered a novel reaction of a cobalt nitrosyl complex that could undergo cycloaddition and cycloreversion with alkenes.

The following mechanism was suggested:

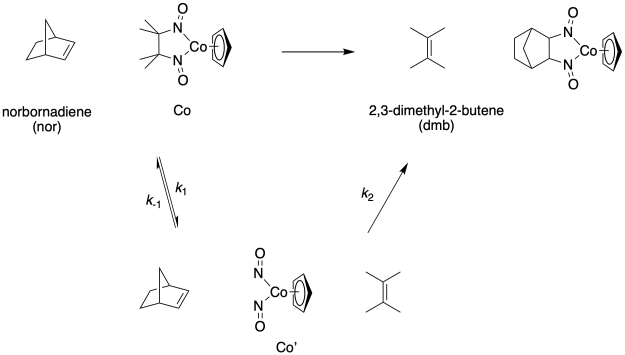
a)  Perform a steady state approximation on Co' to determine the expected rate law.

b)   A plot of the experimentally determined 1/k_obs against [dmb]/[nor] was linear.  Does this experiment match the expectation from the rate law?

References Cited:

1. Schleyer,  P. v. R.; Raber, D. J.; Harris, J. M.; Hall, R. E.  Use of added sodium azide as a mechanistic probe for solovolysis reactions.   J. Am. Chem. Soc. 1971, 93(9), 4821-4828.

2.  Becker, P. N.; Bergman, R. G. Reversible exchange of (.eta.5-cyclopentadienyl)(dinitrosoalkane)cobalt complexes with alkenes. Kinetic and spectroscopic evidence for cyclopentadienyldinitrosylcobalt as a reactive intermediate.  J. Am. Chem. Soc. 1983, 105, 2985-2995.

This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages.  It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. 

Send corrections to cschaller@csbsju.edu

This material is based upon work supported by the National Science Foundation under Grant No. 1043566.

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Back to Mechanistic Determination

Back to Kinetics Index

Back to Reactivity

Back to Structure & Reactivity