Reactivity in Chemistry
Advanced Reaction Kinetics
MK8. The Mathematics Behind Enzyme Kinetics
The Origin of the Michaelis-Menten Equation
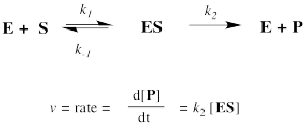
But where does the Michaelis-Menten relationship come from? That takes a little bit of heavy lifting with kinetics. If you feel the need to know, then we'll start with the approximation that the reaction essentially boils down to two steps: substrate binding and the stuff after that. The binding step is described as k1/k-1. The stuff after that is summed up in k2.
The rate of product formation really depends on the rate of the elementary step k2. That rate depends upon the amount of enzyme substrate complex and its rate of passage through the subsequent step.

The trouble is, the enzyme substrate complex is an intermediate. We don't know exactly how much of it we have. We might assume that, as a reactive intermediate, the complex doesn't have much of a lifetime. It gets used up pretty much as soon as it forms.
That assumption helps us to express the concentration of enzyme substrate complex in terms of other things we might know more about: the enzyme and the substrate. Of course, the enzyme and the substrate react together to make the enzyme substrate complex. They react together with rate constant k1.
Two possible fates await the enzyme substrate complex. Either it is released back to enzyme and free substrate, with rate constant k-1, or else it goes on to make product, with rate constant k2. In a steady state approximation, the enzyme substrate complex is consumed as soon as it is formed.
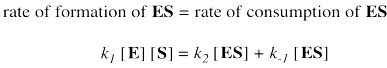
Again, we don't know how much free enzyme there is. We don't know how much enzyme-substrate complex we have. We do know how much enzyme is added at the beginning of the kinetics experiment. We'll call that concentration [Etot], meaning the total amount of enzyme. Some of that enzyme remains free, and some of it is bound as enzyme-substrate complex.
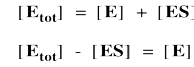
It's useful to express the concentration of free enzyme as the total enzyme minus that portion bound with substrate. That way, we'll be able to eliminate the term for free enzyme from the rate equation. A few steps of algebra let us express the concentration of the enzyme-substrate complex solely in terms of the total enzyme concentration, the substrate concentration and some rate constants.
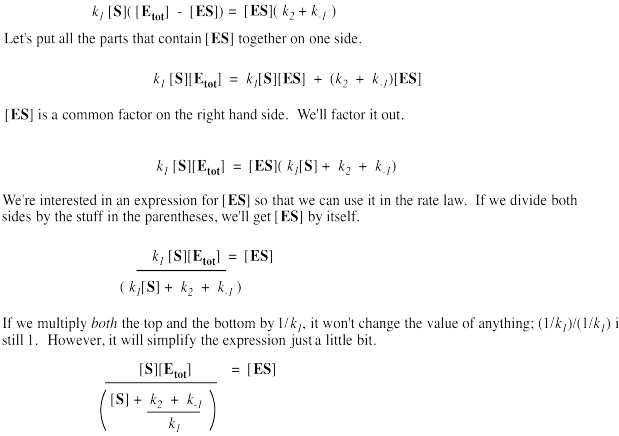
Remember, the rate of product formation just depends on the amount of enzyme-substrate complex and the rate constant for the catalysis step.
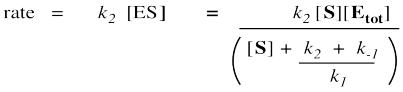
That collection of constants in the denominator is just a group of numbers. It's a constant. We'll call it the Michalis-Menten constant.
![]()
That brings us back to the Michaelis Menten equation.

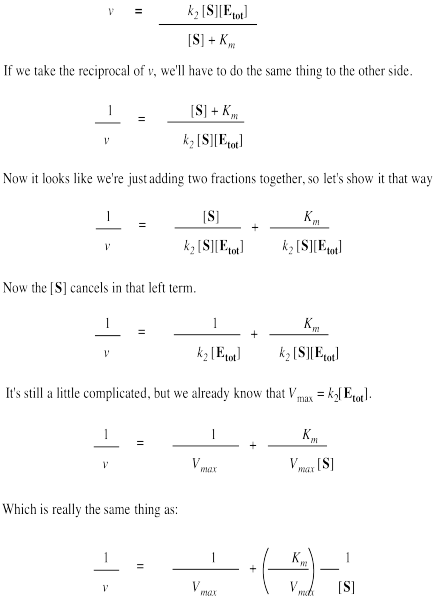
The Lineweaver-Burk equation is arrived at starting from the Michaelis-Menten equation and taking the reciprocal of both sides. Rearranging gives a plot of
This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages. It is freely available for educational use.

Structure & Reactivity in Organic,
Biological and Inorganic Chemistry by
Chris Schaller
is licensed under a
Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
This material is based upon work supported by the National Science Foundation under Grant No. 1043566.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Navigation: