MK6. Enzyme Kinetics:  Michaelis-Menten Plots

An enzyme-catalysed reaction can be roughly divided into three stages: enzyme-substrate binding,  "catalysis" and product release.  "Catalysis" refers to all the steps that happen to convert substrate into product.  Sometimes, these steps are too fast to distinguish from each other.  To simplify, we sometimes refer to this whole sequence of events as though they were just one step.

Figure MK6.1. Equation of reaction for a generalized enzyme-catalyzed reaction.

Often, but not always, that catalysis part is the rate determining step.  Product release is sort of an afterthought.

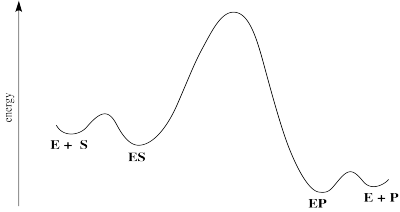
Figure MK6.2. Reaction progress diagram for a generalized enzyme-catalyzed reaction.

In that case, we might simplify and only consider those steps up through catalysis. Here, k₂ is the rate constant for all of the reaction steps after binding, up to the rate-determining step. The reason we do this is just to make the kinetics a little less complicated.

Figure MK6.3. Simplified equation of reaction for an enzyme-catalyzed reaction.

If we do that, we find that enzyme reactions can be summarized by a relation called the Michaelis-Menten equation, named after the early 20th century biochemist Leonor Michaels and his collaborator, the immensely talented artist, physician and biochemist, Maud Menten.

The numerator in this equation should make sense -- of course the rate should increase when we add either more substrate or more enzyme and the relationship will depend on the speed of that product-forming step. Remember, k₂ is just a rate constant that sums up the steps after substrate binding. It is sometimes called k_cat, or the rate constant for catalysis.

The denominator is a little more complicated and contains the composite constant K_m, the Michaelis-Menten constant.

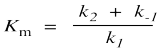
The Michaelis-Menten constant is related to enzyme-substrate binding, although the relationship is subtle. If we think about that first step in any enzyme-catalyzeed reaction, substrate binding, we can imagine there being an equilibrium between the free substrate plus enzyme (E + S) and the bound enzyme-substrate complex (ES). We can think about the equilibrium in terms of concentration ratios: K_binding = K_assoc = [ES]/[E][S]. The equilibrium constant for binding is seen in the ratio of bound complex to free enzyme and substrate at equilibrium. The tighter the substrate is bound, the greater that ratio will be. We can also think about the equilibrium in terms of how quickly the enzyme-substrate complex forms, compared to how quickly that complex comes apart again. We call this concept "kinetic approach to equilibrium": K_assoc = k₁/k_-1.

That relationship doesn't directly help us understand what K_m tells us, but it gets us a step closer. K_m has k_-1 in the numerator (on top of the fraction) and k₁ in the denominator (on the bottom of the fraction). That's the opposite of K_assoc, which has k₁ in the numerator and k_-1 in the denominator. K_m looks a little more like the equilibrium constant for the opposite reaction, dissociation of the enzyme-substrate complex to give free enzyme and free substrate: K_dissoc> = k_-1/k₁. We might say that K_m roughly resembles a dissociation constant. Whereas an association constant tells us how tightly something binds, a dissociation constant just flips that relationship over, telling us how easily something that's already bound can be released. In a rough way of speaking, K_dissoc tells us looseness of binding. The larger the value of K_dissoc, the more loosely the substrate is bound, and the more easily it is released.

K_m is a little different from K_dissoc because it also contains k₂. It isn't exactly the same as the dissociation constant. However, in some situations, it becomes closer to the dissociation constant. Notice that if k_-1 is much larger than k₂, then k₂ + k_-1 is roughly k_-1. If we are adding two numbers together and one number is much bigger than the other one, then the sum is pretty close to the bigger number. In that case, we can just ignore the smaller number in that sum. If we do that, then under those conditions, K_m = K_dissoc. Sometimes, we will describe this situation as a limiting case. We look for a specific case under which the kiteics simplifies to give us more information. In this case, the Michalis-Menten products is similar to the dissociation constant when the rate of dissociation is high compared to the rate of the subsequent reaction. That would happen if the barrier to substrate binding and release was pretty low compared to the barrier for reaction. That's exactly what our reaction progress diagram looks like. It doesn't describe all cases, but it gives us a useful way to think about this constant.

• k₂ or k_cat describes the rate of reaction after substrate binding.
• The larger the value of k₂, the faster the enzyme-catalyzed reaction.
• K_m is related to the dissociation constant for the enzyle-substrate complex.
• The smaller the value of K_m, the more tightly the enzyme binds substrate, making the enzyme-catalyzed reaction more efficient.

The Michaelis-Menten relationship can also be understood most easily by examining its limits.  For instance, suppose the substrate concentration is still very low.  Perhaps it is much smaller than K_m.  How does that affect the rate of the reaction?

It is useful to keep in mind that a large number added to a small number is just a large number.  One million plus one is about a million.  One million plus three is also about a million.  One million plus five is pretty close to a million.  We can often ignore the small quantity in additions.  In that sense, if [S] is small, we can ignore it in the denominator, and think of the denominator instead as "approximately K_m".

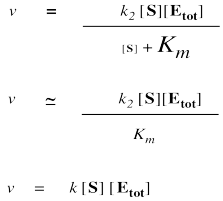
We can't ignore [S] in the numerator, of course, even if it is very small.  That's because a number multiplied by a very small number also becomes a very small number; the small number really counts when it is multiplied by something.

On the other hand, when [S] gets very large, we can ignore Km.  That means Km disappears from the denominator, leaving only [S].  At that point, the [S] in the denominator and numerator cancels.

Remember, when [S] gets very large, the reaction has reached its maximum possible rate, because the enzyme is saturated.  Adding more substrate doesn't speed things up, because the extra substrate just has to wait around until an enzyme becomes available.  We call that maximum rate V_max.

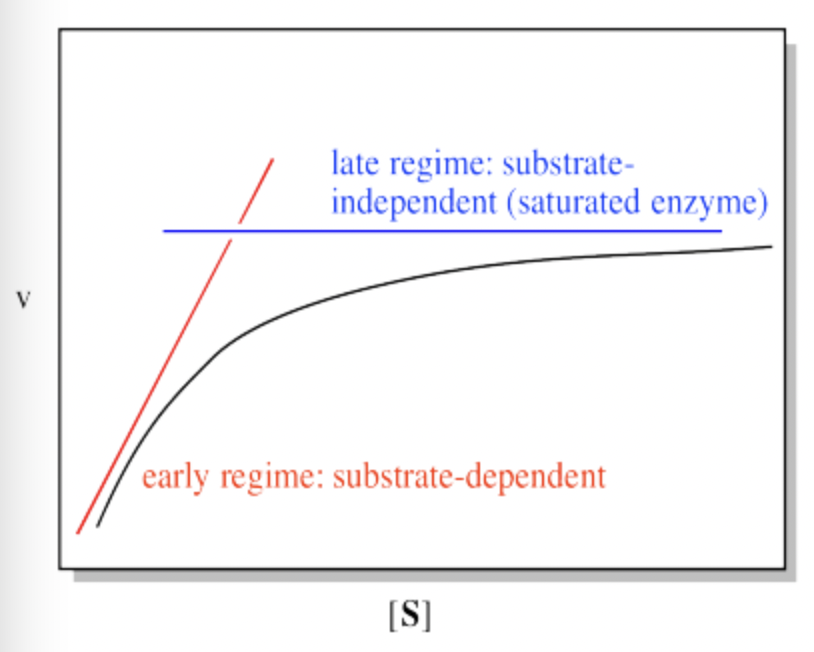
Figure MK6.4. Two regimes in the plot of rate vs substrate concentration.

• The limits of the Michaelis Menten equation explains the shape of the curve describing the rate dependence on substrate.

There is another piece of useful information we can get from this equation.  It comes at an intermediate point between the two cases we have considered so far.  What if the numerical value of K_m and [S] are exactly equal?  In that case, the value of the denominator, K_m + [S], is the same as [S] + [S].  The denominator becomes 2[S].  Just as in the limiting case that gave us the value of V_max, the [S] cancels, but this time there is still a 2 in the denominator, so we get V_max/2. 

Turning that conclusion around, if we find the point on a Michaelis Menten plot where the rate is half the maximum rate, we can drop a line down to the x axis.  The value of [S] at the intercept will be numerically the same as the value of Km.

• V_max is the point on the y axis where the rate has completely leveled off.
• K_m is the point on the x axis corresponding to y = V_max/2.

Problem MK6.1.

Determine V_max and K_m in each of the following cases.  Assume the units of [S] are millimoles per liter and the units of V are moles per liter per second.

a)

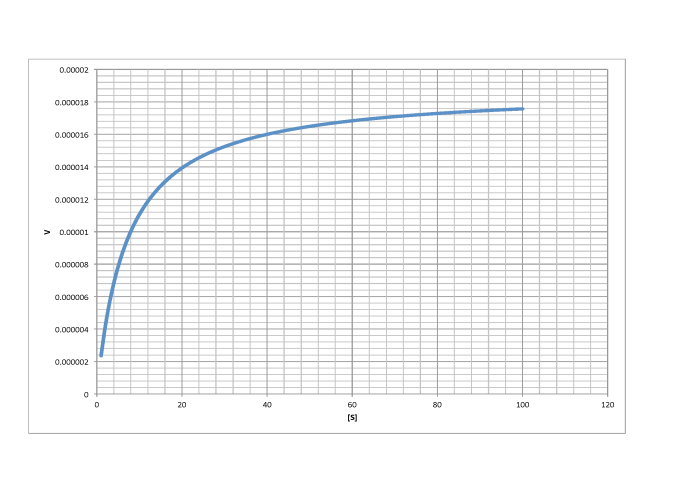
b)

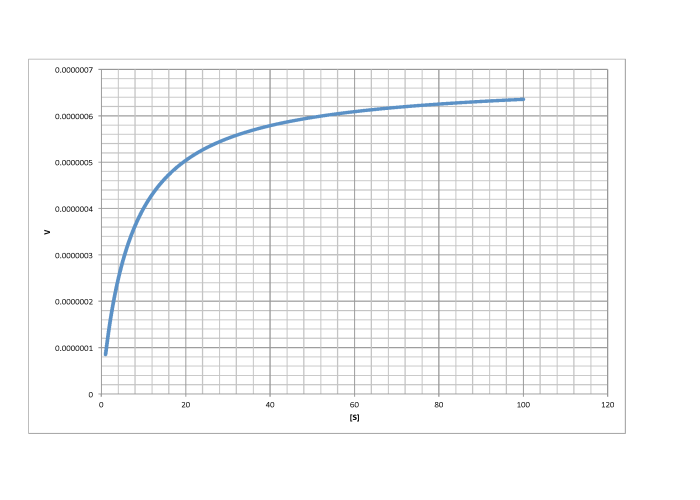
c)

d)

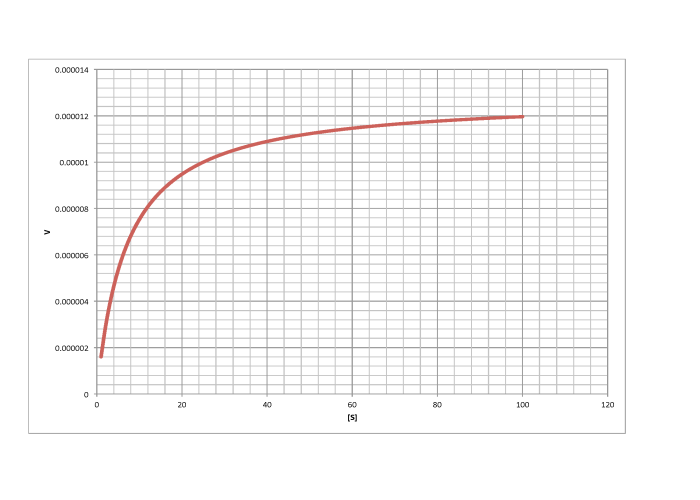
e)

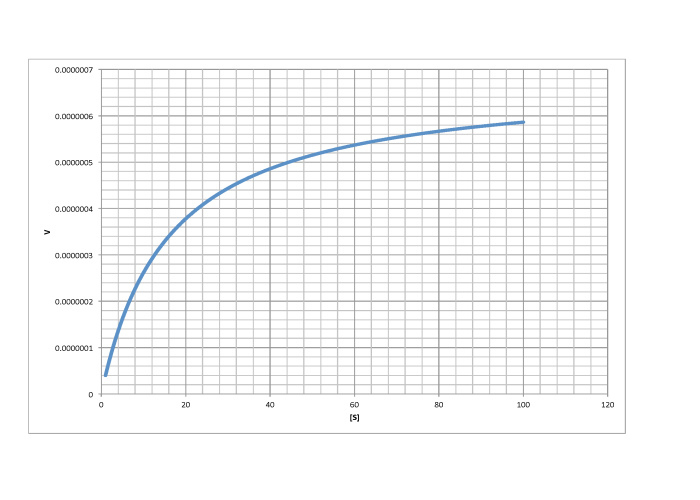
Turnover Frequency and Efficiency

If we're running an experiment, we know what the total concentration of enzyme is, because we're the ones who put it in there.  That means that we can also figure out exactly what that rate constant is for catalysis.

k_cat = k₂ = V_max / [E_tot]

That quantity, k_cat, is sometimes referred to by biochemists as the "turnover number".  The turnover number essentially means the number of molecules of product made by an enzyme in the specified period of time (usually the units of k_cat are expressed as s^-1, but they could also be written in min^-1, etc).

In industrial catalysis,  k_cat  is instead referred to as the "turnover frequency", but of course it still means the same thing.  There is an important reason for this difference in terms.  The "turnover number" in industry refers to the number of molecules of product made before the catalyst stops working.  Catalyst death can occur for any number of reasons, but you might imagine something going wrong via a side reaction that renders the catalyst unreactive toward the substrate.  This is a very important consideration in industry.  The engineer in charge of the production plant would like to replace the catalyst with a new batch before it stops working, to avoid an unscheduled halt in the process that could prove very costly.  They need to have an idea about when that is likely to happen, so they need to be aware of the turnover number in this sense.

Another consideration that is sometimes useful is enzymatic efficiency.  Remember, the reaction does not depend only on the catalysis step.  The binding step also matters.  The faster the catalysis step, the faster the production of product.  In addition, the greater the proportion of substrate bound, the faster the production of product.

Combining those two ideas:

Efficiency = k_cat / K_m

In this relationship, K_m is a stand-in for the equilibrium constant for enzyme-substrate dissociation.  It's not quite the same thing, but it's the closest we've got.  By extension, 1/K_m stands for the enzyme-substrate binding constant.  The greater the binding constant and the faster the catalysis, the more efficient the enzyme. 

Note that the units of K_m are concentration units (mol L^-1, for instance).  The units of efficiency will therefore be something like L mol^-1 s^-1.

Problem MK6.2.

In a simplified enzyme-catalyzed mechanism, k₁ represents the elementary rate constant for binding enzyme to substrate; k_-1> represents the reverse step, dissociation of substrate from enzyme. Calculate K_dissoc, the dissociation constant of the enzyme-substrate complex, for the following cases.

a) k₁ = 0.0101 M s^-1; k_-1 = 0.00765 s^-1

b) k₁ = 0.197 M s^-1; k_-1 = 0.321 s^-1

c) k₁ = 0.775 M s^-1; k_-1 = 0.542 s^-1

d) k₁ = 0.499 M s^-1; k_-1 = 0.0228 s^-1

Problem MK6.3.

In a simplified enzyme-catalyzed mechanism, k₁ represents the elementary rate constant for binding enzyme to substrate; k_-1> represents the reverse step, dissociation of substrate from enzyme; and k₂ represents the forward reaction and product release steps. Calculate K_m for the following cases.

a) k₁ = 0.0101 M s^-1; k_-1 = 0.00765 s^-1; k₂ = 0.00654 s^-1

b) k₁ = 0.197 M s^-1; k_-1 = 0.321 s^-1; k₂ = 0.000065 s^-1

c) k₁ = 0.775 M s^-1; k_-1 = 0.542 s^-1; k₂ = 0.234 s^-1

d) k₁ = 0.499 M s^-1; k_-1 = 0.0228 s^-1; k₂ = 0.0087 s^-1

Problem MK6.4.

In the following cases, compare K_m to K_dissoc if k₁ represents the elementary rate constant for binding enzyme to substrate; k_-1> represents the reverse step, dissociation of substrate from enzyme; and k₂ represents the forward reaction and product release steps.

a) k₁ = 0.326 M s^-1; k_-1 = 0.195 s^-1; k₂ = 0.00038 s^-1

b) k₁ = 0.326 M s^-1; k_-1 = 0.195 s^-1; k₂ = 0.723 s^-1

c) k₁ = 0.326 M s^-1; k_-1 = 0.195 s^-1; k₂ = 0.00239 s^-1

d) k₁ = 0.326 M s^-1; k_-1 = 0.195 s^-1; k₂ = 0.0345 s^-1

Problem MK6.5.

Calculate k_cat in each of the following cases:

a) v_max = 125.3 µM min^-1; [E] = 31.5 pM

b) v_max = 1.587 mM min^-1; [E] = 7.04 pM

c) v_max = 3.21 nM min^-1; [E] = 0.0129 pM

d) v_max = 0.129 µM min^-1; [E] = 2.27 pM

These metric conversions may be useful:

1 pmol = 10^-12 mol

1 nmol = 10^-9 mol

1 µmol = 10^-6 mol

1 mmol = 10^-3 mol

Problem MK6.6.

Calculate catalytic efficiency in each of the following cases:

a) k_cat = 409 min^-1; K_m = 31.5 nM

b) k_cat = 22.6 min^-1; K_m = 1.56 mM

c) k_cat = 1.76 min^-1; K_m = 17.4 mM

Problem MK6.7.

In each of the following cases, V was measured in nmol L^-1 s^-1 and [S] was measured in nmol L^-1. Calculate v_max and K_m from the fit to a straight line, y = mx + b, obtained in the Lineweaver-Burk plot in each case.

a) y = 0.00326x + 0.129

b) y = 0.0759x + 0.0957

c) y = 0.000434x + 0.765

This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages.  It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. 

Send corrections to cschaller@csbsju.edu

This material is based upon work supported by the National Science Foundation under Grant No. 1043566.

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Navigation:

Back to Kinetics

Back to Reactivity Index

Back to Mechanistic Determination

Back to Structure & Reactivity Web Materials