OP7. Solutions for Selected Problems

Problem OP2.1.

Problem OP2.2.

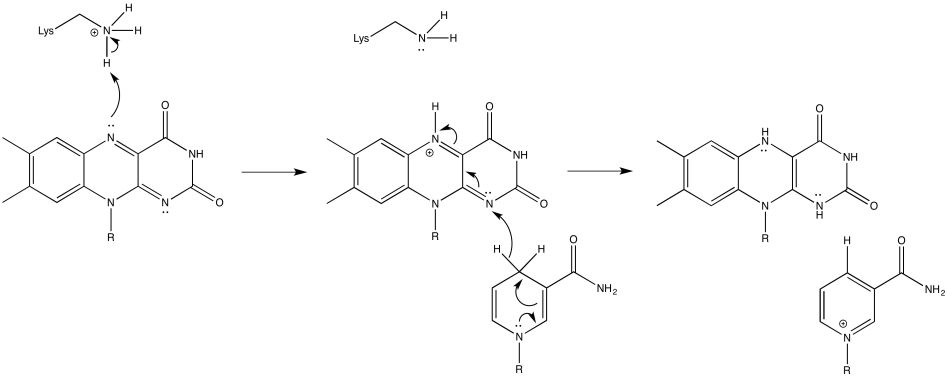
Problem OP2.3.

a)  Iron charges:   Fe(II) + Fe(III) = 5⁺

     Ligand charges:  2 sulfides = 2 x 2^-   = 4^- ; 4  cysteines = 4 x 1^- = 4^- ;  total = 8^-

     Overall:  3^- 

b)  Iron charges:   2 x Fe(II) + Fe(III) = 4⁺  +   3⁺  = 7⁺

     Ligand charges:  4 sulfides = 4 x 2^-   = 8^- ; 3  cysteines = 3 x 1^- = 3^- ;  total = 11^-

     Overall:  4^- 

c)  Iron charges:   3 x Fe(II) + Fe(III) = 6⁺  +   3⁺  = 9⁺

     Ligand charges:  4 sulfides = 4 x 2^-   = 8^- ; 4  cysteines = 4 x 1^- = 4^- ;  total = 12^-

     Overall:  3^- 

Problem OP2.4.

Upon reduction, the charge on a 2Fe2S cluster will increase from 3^- to 4^-, assuming it starts in a mixed Fe(II)/(III) state (whereas if it starts in a Fe(III)/(III) state, the overall charge will increase from 2^- to 3^-).  These anions would be stabilised by strong intermolecular interactions such as ion-dipole forces.  Both states (oxidised and reduced) will be stabilised by a polar environment, but the more highly charged reduced state will depend even more strongly on stabilisation by the environment.  As a result, we might expect the reduction potential to be lower when surrounded by nonpolar amino acid residues, and higher if surrounded by polar residues.

Problem OP2.5.

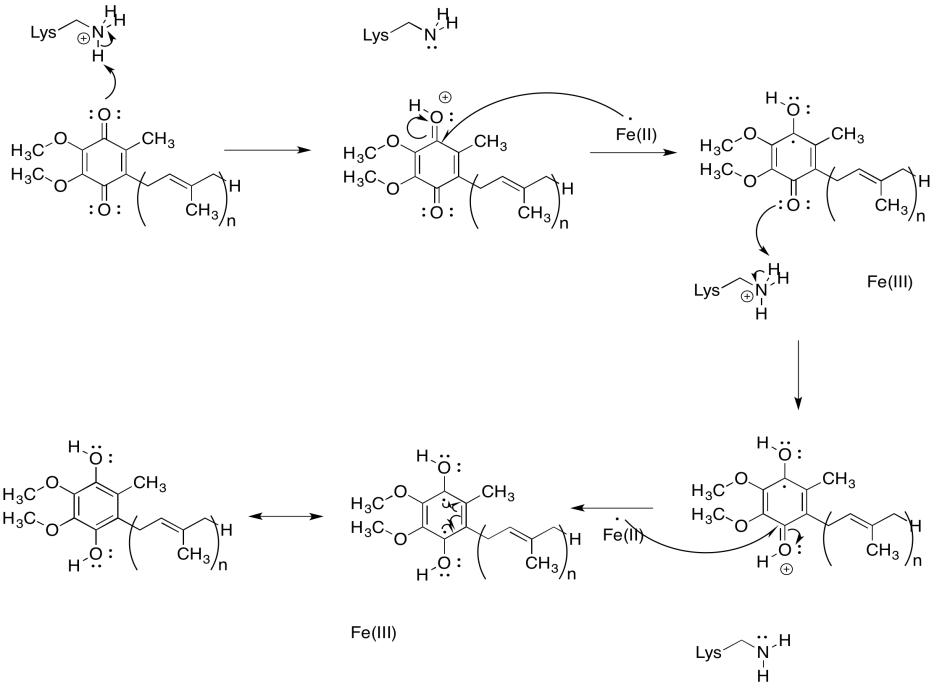
Problem OP2.6.

Problem OP2.7.

Problem OP2.8.

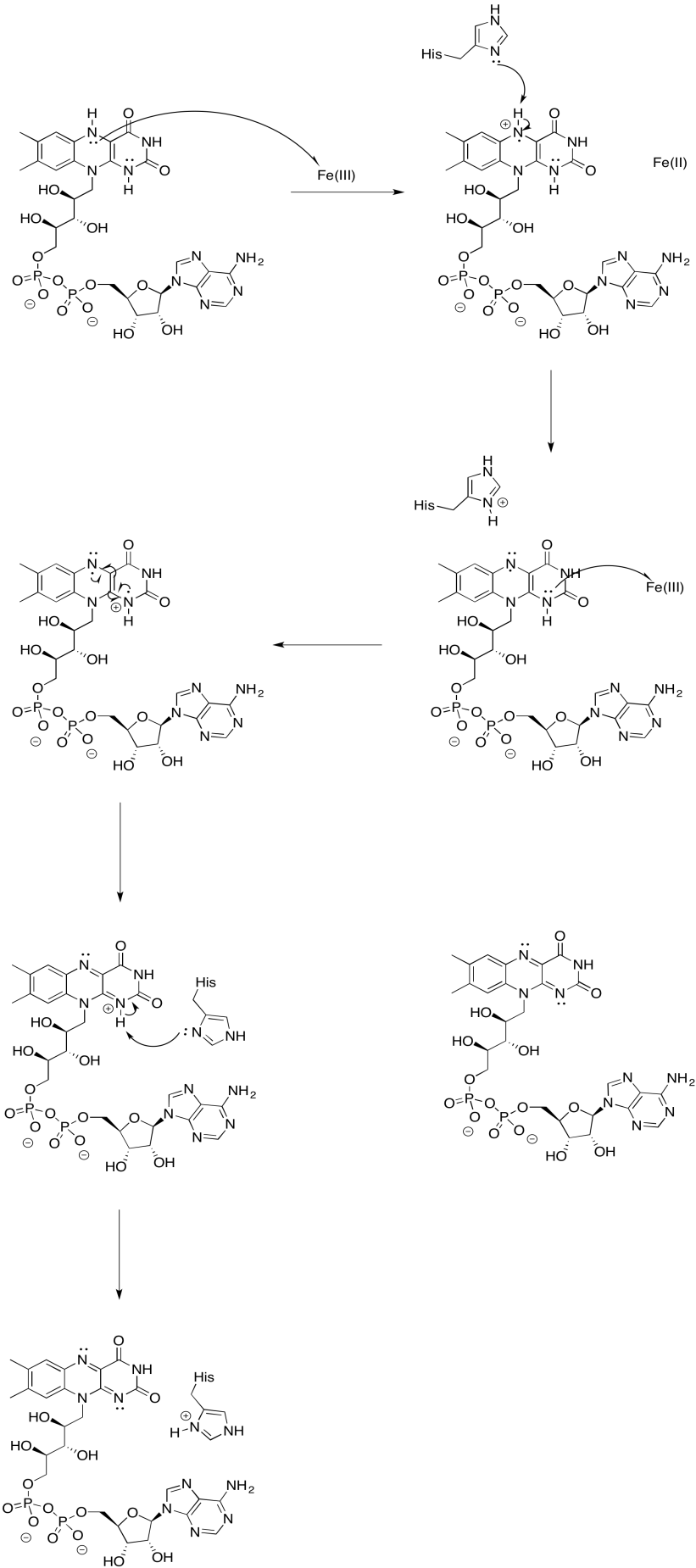
Problem OP2.9.

a)  N1a and N1b are most likely not involved, because their reduction potentials are too negative.

b)

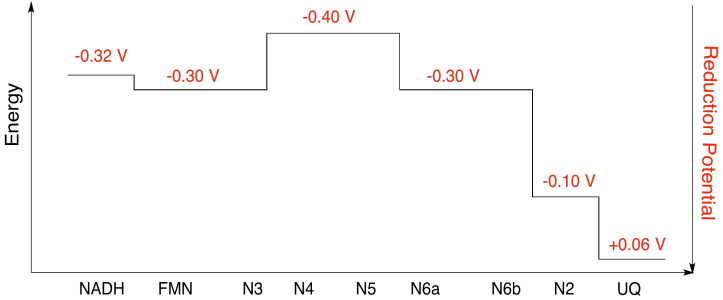
Problem OP2.10.

Assuming the reduction potentials are:

N5(ox)  +  e^-     →  N5(red)        E^o_red = -0.40 V

N6a(ox)  +  e^-     →  N6a(red)        E^o_red = -0.30 V

Then the potential difference for the reaction, ΔE^o = -0.30 - (-0.40) V = 0.10 V.

The Faraday relation ΔG = - n F ΔE^o   gives

 ΔG = - 1 x 96,485 J V^-1 mol^-1 x 0.10 V = 9,649 J mol^-1  = 9.7 kJ mol^-1  

Problem OP3.1.

Heme b.

Problem OP3.2.

A porphyrin contains four pyrrole rings (five-membered, aromatic ring containing a nitrogen) arranged to form a 16-membered macrocycle.

Problem OP3.3.

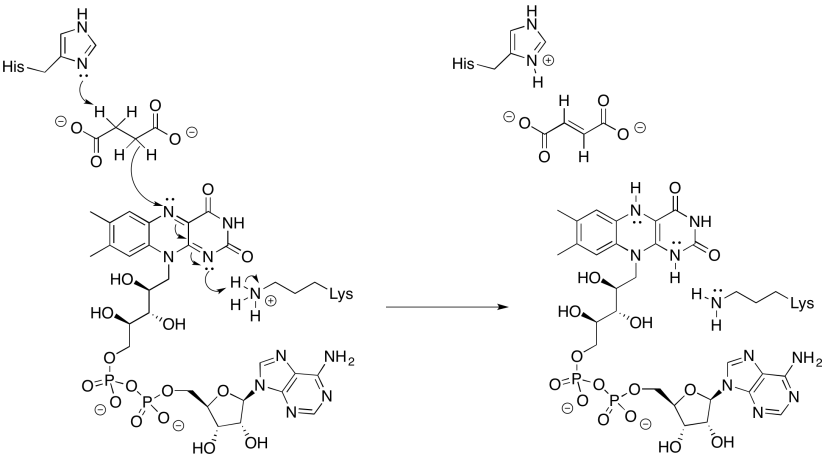
Problem OP3.4.

Problem OP3.5.

Assuming the reduction potentials are:

4Fe4S(ox)  +  e^-     →  4Fe4S(red)        E^o_red = -0.15 V

3Fe4S(ox)  +  e^-     →  3Fe4S(red)        E^o_red = 0.06 V

Then the potential difference for the reaction, ΔE^o = 0.06 - (-0.15) V = 0.21 V.

The Faraday relation ΔG = - n F ΔE^o   gives

 ΔG = - 1 x 96,485 J V^-1 mol^-1 x 0.21 V = 20,262 J mol^-1  = 20 kJ mol^-1  

Problem OP3.6.

a)  Iron charges:   2 x Fe(III) = 6⁺

     Ligand charges:  2 sulfides = 2 x 2^-   = 4^- ; 4  cysteines = 4 x 1^- = 4^- ;  total = 8^-

     Overall:  2^- 

b)  Iron charges:   3 x  Fe(III) = 9⁺

     Ligand charges:  4 sulfides = 4 x 2^-   = 8^- ; 3  cysteines = 3 x 1^- = 3^- ;  total = 11^-

     Overall:  2^- 

c)  Iron charges:   4 x Fe(III)  = 12⁺

     Ligand charges:  4 sulfides = 4 x 2^-   = 8^- ; 4  cysteines = 4 x 1^- = 4^- ;  total = 12^-

     Overall:  0

Problem OP4.1.

Arninine and lysine are positively charged at neutral pH.

Problem OP4.2.

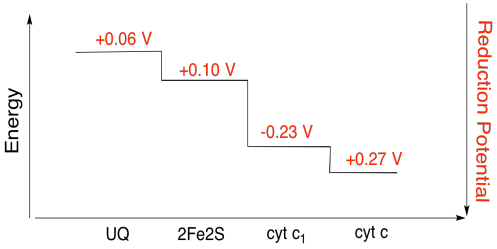
Problem OP4.3.

Assuming the reduction potentials are:

2Fe2S(ox)  +  e^-     →  2Fe2S(red)        E^o_red = 0.10 V

cyt c₁(ox)  +  e^-     →  cyt c₁(red)        E^o_red =  0.230 V

Then the potential difference for the reaction, ΔE^o = 0.23 - (0.10) V = 0.13 V.

The Faraday relation ΔG = - n F ΔE^o   gives

 ΔG = - 1 x 96,485 J V^-1 mol^-1 x 0.13 V = 12,543 J mol^-1  = 12.5 kJ mol^-1  

Problem OP4.4.

The positive arginine residues would confer partial positive charge on the ubiquinone via hydrogen bonding; the ubiquinone would have a more positive reduction potential as a result.

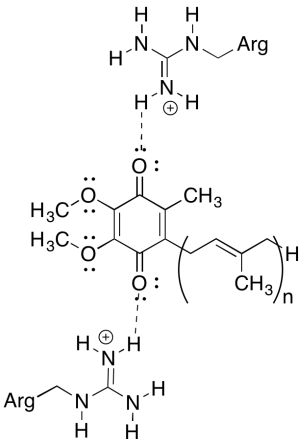
Problem OP5.1.

O₂  →  H₂O

O₂  →  2 H₂O   (O balanced)

O₂ + 4H⁺ →  2 H₂O   (H balanced)

O₂ + 4e^-  + 4H⁺  →   2 H₂O  (charge balanced)

Problem OP5.2.

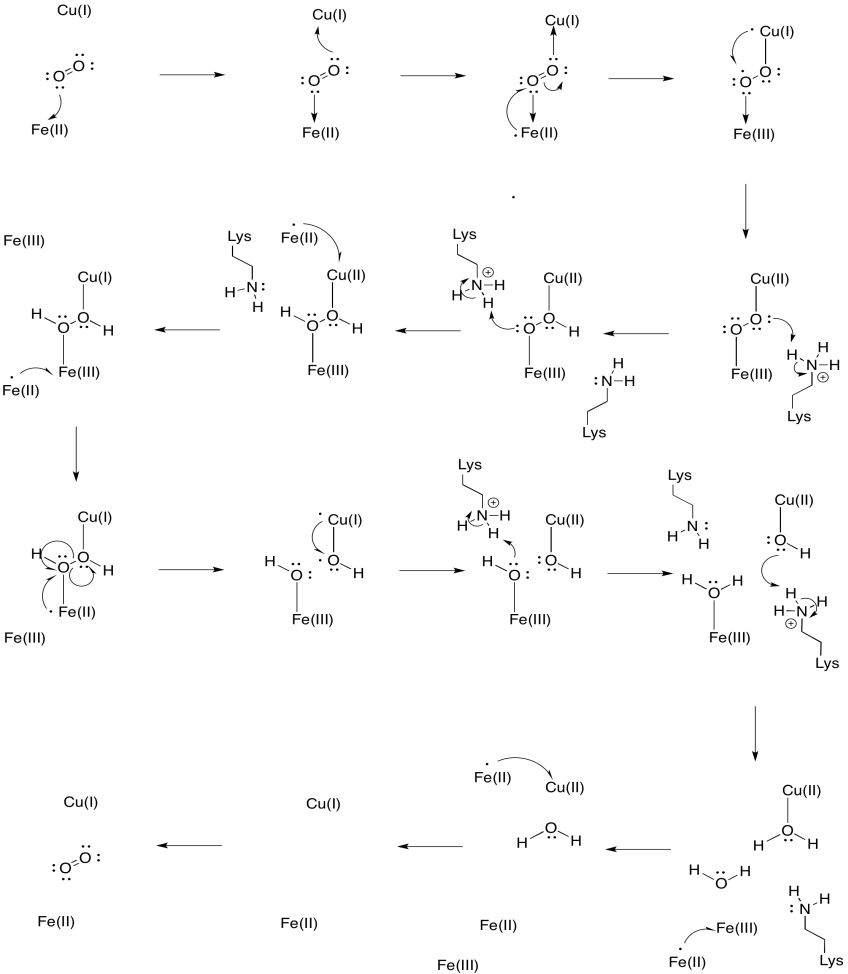
Problem OP5.3.

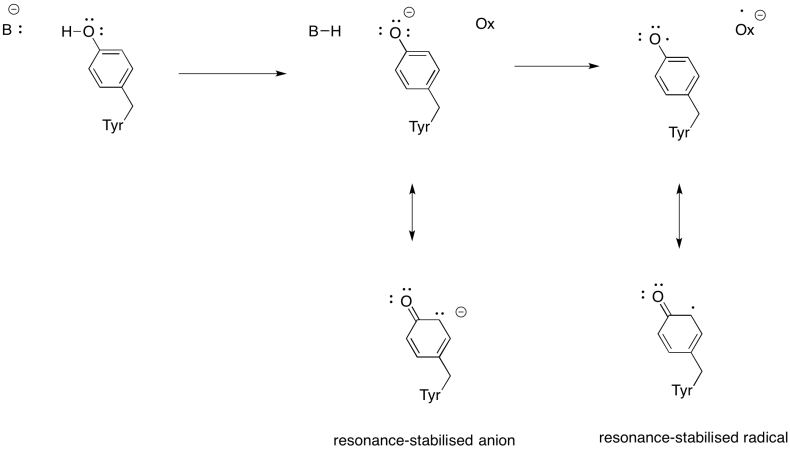
Problem OP5.4.

a) 

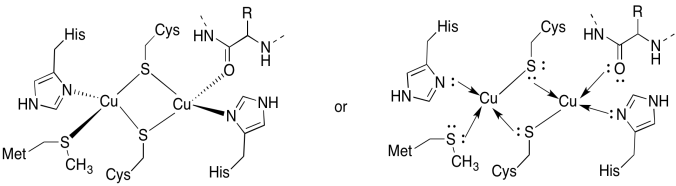
b) tetrahedral

c) Cu(I) = d¹⁰

    4 donors = 8 e^-

    total = 18e^- 

d) 2 x Cu(I) = 2⁺

    2 x Cys-S^- = 2^-

    All others neutral

   Total = 0 

Problem OP5.5.

a)

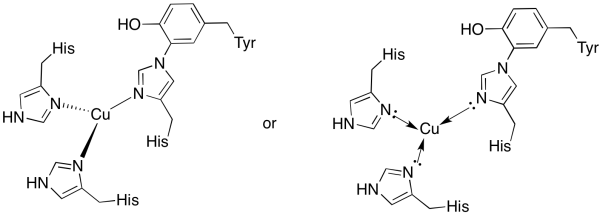
b) trigonal planar

c) Cu(I) = d¹⁰

     3 donors = 6 e^-

     total = 16 e^- 

d) Cu(I) = 1⁺

    histidines neutral

   Total = 1⁺ 

Problem OP5.6.

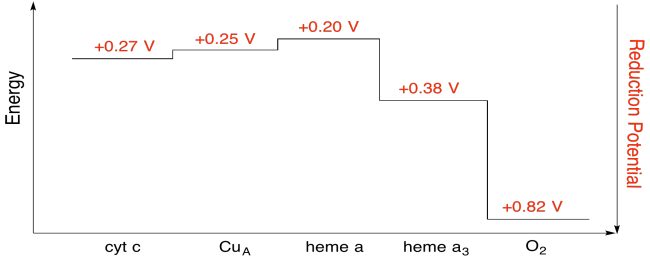
Problem OP5.7.

Assuming the reduction potentials are:

heme a(ox)  +  e^-     →  heme a(red)        E^o_red = 0.20 V

heme a₃(ox)  +  e^-     →  heme a₃(red)        E^o_red =  0.38 V

Then the potential difference for the reaction, ΔE^o = 0.38 - (0.20) V = 0.18 V.

The Faraday relation ΔG = - n F ΔE^o   gives

 ΔG = - 1 x 96,485 J V^-1 mol^-1 x 0.13 V = 17,367 J mol^-1  = 17.4 kJ mol^-1  

Problem OP6.1.

These amino acids would probably be non-polar: alanine, glycine, methionine, isoleucine, leucine, methionine, phenylalanine, tryptophan, valine.

Problem OP6.2.

There is always an equilibrium between the protonated state and the deprotonated state in a charged amino acid residue.  For this position, an amino acid is needed that is more reliably in the protonated state; that is, the equilibrium lies more heavily to the protonated side of the equation.  Because of the resonance-stabilised cation that results from protonation, arginine is much more likely to remain in a protonated state than lysine.  That will make for a more efficient millwheel.

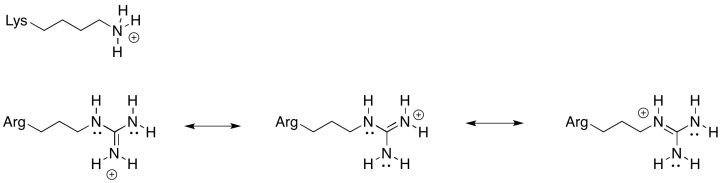
Problem OP6.3.

ADP and phosphate are both anions; they would repel normally each other.  When bound in the active site, their charges are likely neutralized by complementary charges in the active site.

Problem OP6.4.

Assuming the reduction potentials are:

NAD⁺  +  2e^-  + 2 H⁺   →  NADH        E^o_red = -0.32 V

0.5 O₂  +  2e-  + 2 H+   →  H₂O        E^o_red = 0.816 V

Then the potential difference for the reaction, ΔE^o = 0.816 - (-0.32) V = 1.136 V.

The Faraday relation ΔG = - n F ΔE^o   gives

 ΔG = - 2 x 96,485 J V^-1 mol^-1 x 1.136 V = 219,213 J mol^-1  = 219 kJ mol^-1

so 219 kJ mol^-1 / 30 kJ mol^-1 = 7.3

With 100% efficiency, 7 moles of ATP could be produced per mole of NADH.  In reality, about half that amount is produced (closer to 3 moles ATP per mole NADH).

This site is written and maintained by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with contributions from other authors as noted.  It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. 

This material is based upon work supported by the National Science Foundation under Grant No. 1043566.

Navigation:

Back to Oxidative Phosphorylation

Back to Reactivity Index

Back to Structure & Reactivity Web Materials