Reactivity in Chemistry
Reduction & Oxidation Reactions
RO5. Factors Influencing Redox Potential: Thermodynamic Cycles
In general, the ions of very late transition metals -- those towards the right-hand end of the transition metal block, such as copper, silver and gold -- have high reduction potentials. In other words, their ions are easily reduced. Alkali metal ions -- on the very left edge of the periodic table, such as potassium or cesium -- have very negative reduction potentials. These ions are very difficult to reduce. These trends are not surprising, because alkali metals are generally at the lower end of the electronegativity scale and are typically found as cations, not as neutral atoms. Late transition metals are comparatively electronegative in this case, and so we would expect their ions to attract electrons more easily than alkali metal ions.
The nice thing about redox is you can always look at it from either direction. Oxidation is simply the opposite of reduction. How easily does an alkali metal lose an electron? If the standard reduction potential of lithium is very negative, then the oxidation potential of lithium ion is very positive. If it is uphill to transfer an electron from hydrogen to lithium cation, it must be downhill to transfer an electron from a lithium atom to a proton. After all, hydrogen is more electronegative than any of the alkalis. Of course, since a late transition metal is generally more electronegative than an alkali metal, copper or silver or gold ought to be more difficult to oxidize than sodium or potassium.
The large trends in redox chemistry are not surprising, then. It's simply a matter of the electron moving to a lower energy level on another atom.
If we look a little more closely, though, there are plenty of exceptions to the general trend. For example, in the coinage triad, gold has the most positive reduction potential, followed by silver, then copper. That's exactly the opposite of expectations; copper, at the top of the column, should be the most electronegative and have the most positive reduction potential, not the least. What's going on in those cases?
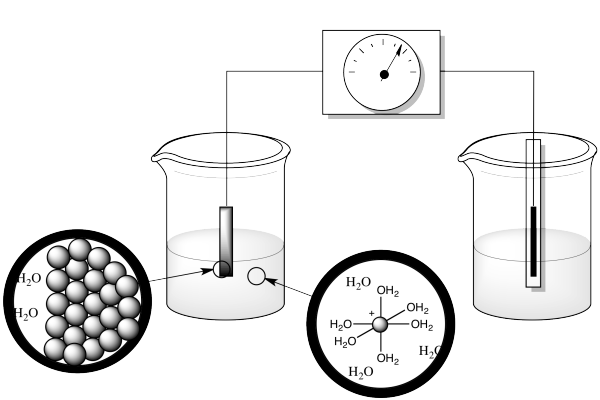
Well, there's more going on than just moving an electron. Remember, in the measurement of a reduction potential, we are generally working with a metal electrode in an aqueous solution of ions.

Figure RO5.1. A "microscopic" or nanoscopic view of two sides of a redox half-reaction.
What else is going on in this reaction? Well, the atom that gets reduced starts out as an ion in water, but an ion in water doesn't sit around on its own. It's a Lewis acid, an electrophile. Water is a nucleophile, a potential ligand. So the ion in solution is actually a coordination complex. It swims around for a while, then bumps into the cathode, where it picks up the electron. But the resulting ion doesn't stay in solution; it gets deposited at the electrode, along with others of its kind. It becomes part of a metal solid.
So there are three different things happening here: ligand dissociation, electron transfer and solid formation. If we could get some physical data on each of those events, we might be able to explain why these reduction potentials are contrary to expectations.
The kinds of data we have available for these individual steps may actually fit the opposite reaction better. We can estimate the energy involved in the removal of a metal atom from the solid, the loss of an electron from the metal, and the binding of water to the resulting ion. These data come from measurement of the heat of vaporization of the metal, the ionization energy of the metal, and the enthalpy of hydration of the metal.
We can use these data to construct a thermodynamic cycle. The cycle describes an alternate pathway from copper metal to aqueous Cu(I) ion. The alternative pathway, if we've chosen it correctly, ought to give us a pretty good idea of the enthalpy change involved in the reduction of copper.
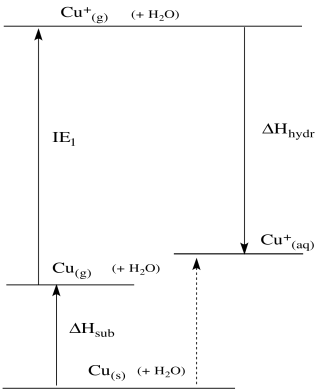
Figure RO5.2. A thermodynamic cycle for the oxidation of Cu(s) to CuI(aq).
The trouble is, these data all involve the gas phase. If they really applied to this situation, it would be as if metal atoms sprayed out into the air above the electrode, shot their electrons back, grabbed some water molecules that drifted by, and then dropped down into the solution. Of course that doesn't happen; we don't see a little, sparkly, metallic mist appear when we connect the circuit, or little lightning bolts from the cloud of metal atoms to the electrode, and we don't see a splash or a fizz or little tendrils of steam as the resulting ions drop into the water.
That doesn't matter. The data we have here are still very useful. That's because what we are looking at -- the energy difference between two states -- is a state function. That means it doesn't matter how we get from one state to the other; the overall difference will always be the same. So if the reaction did happen via the gas phase, the energy change would be exactly as it is when it happens directly at the electrode - solution interface. We can do a sort of thought experiment using the data we know, and even though those steps don't really happen the way they do in the experiments that gave rise to the data, they will eventually lead to the right place. This sort of imaginary path to mimic a reaction we want to know more about employs an idea called "Hess's Law". It is frequently used to gain insight into reactions throughout chemistry.
Here are the data for copper, silver and gold.
Table RO5.1. Values for a thermodynamic cycle that models a redox half-reaction.
| element | copper | silver | gold |
| reduction potential, Eo, V | +0.520 | +0.7996 | +1.83 |
| 1st ionization energy, kJ/mol | 745.5 | 731 | 890 |
| heat of sublimation, kJ/mol | 313 | 265 | 355 |
| enthalpy of hydration, kJ/mol | -593 | -473 | -615 |
| covalent radius, Angstroms | 1.32 | 1.45 | 1.36 |
Taking all of these data together, we can get a better picture of the overall energy changes that would occur during a reduction or, more directly, an oxidation.
The first thing to note is that copper has a higher ionization energy than silver. As expected, Cu+ really is harder to form than Ag+, because copper is more electronegative than silver. But wait a minute -- Au+ appears to be the hardest to form of all three. It's as if gold were the most electronegative of these three elements -- but it's at the bottom of this column.
Gold really is more electronegative than copper or silver. Take a look at the electronegativity chart below.
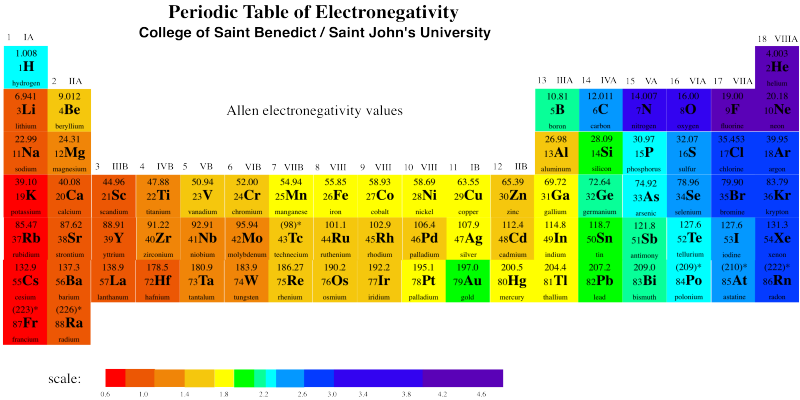
Figure RO5.3. A periodic table showing electronegativity trends.
There are a few deviations from expectation in periodic trends, but this one is probably attributable to a phenomenon called "the lanthanide contraction". Notice the covalent radii of gold and silver in the table above. Normally, we expect atoms to get bigger row by row, as additional layers of electrons are filled in. Not so for the third row of transition metals. To see the probable reason for that, you have to look at the whole periodic table, and remember for the first time ever that the lanthanides and actinides -- the two orphaned rows at the bottom -- actually fit in the middle of the periodic table. The lanthanides, in particular (lanthanum, La, to ytterbium, Yb), go in between lutetium (Lu) and Hafnium (Hf).
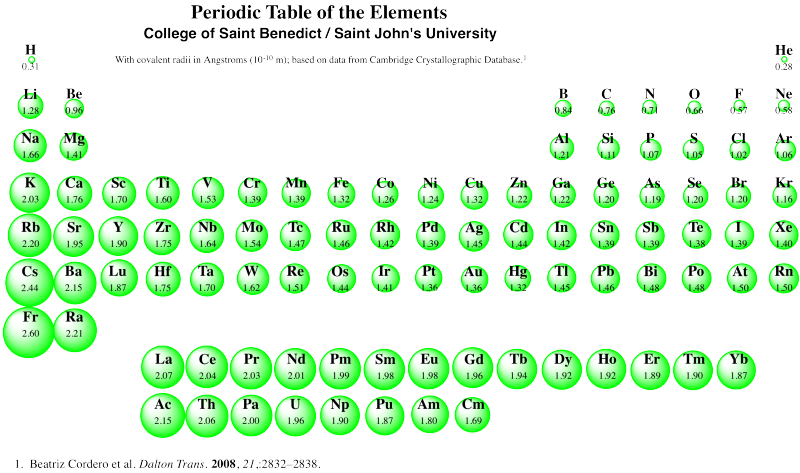
Figure RO5.4. A periodic table showing trends in covalent radii.
As a result, the third row of transition metals contain many more protons in their nuclei, compared to the second row transition metals of the same column. Silver has ten more protons in its nucleus than rubidium, the first atom in the same row as silver, but gold has twenty four more than cesium. The third row "contracts" because of these additional protons.
So the exceptionally positive reduction potential of Au+ (and, by relation, the exceptionally negative oxidation potential of gold metal)may be a result of the lanthanide contraction.
What about copper versus silver? Copper still has a higher electronegativity than silver, but copper metal is more easily oxidized. It's not that copper is more easily pulled away from the metallic bonds holding it in the solid state; copper's heat of vaporization is a little higher than silver's. That leaves hydration. In fact, copper ion does have a higher enthalpy of hydration than silver; more energy is released when water binds to copper than when water binds to silver. The difference between these two appears to be all about the solvation of the copper ion, which is more stable with respect to the metal than is silver ion.
Why would that be? Well, copper is smaller than silver. A simple look at Coulomb's law reminds us that the closer the electrons of the donor ligand are to the cation, the more tightly bound they will be. Looking at it a slightly different way, copper is smaller and "harder" than silver, and forms a stronger bond with water, which is a "hard" ligand.
Taking a look at a Hess's Law cycle for a redox reaction is a useful approach to get some additional insight into the reaction. It lets us use data to assess the influence of various aspects of the reaction that we can't evaluate directly from the reduction potential, because in the redox reaction all of these factors are conflated into one number.
Problem RO5.1.
Compare the reduction potentials of lithium, sodium and potassium ions. Can you use data on heat of vaporization, ionization energy and enthalpy of solvation to determine what factors are responsible for the order of ease of oxidation of these metals?
Problem RO5.2.
Compare the reduction potentials of copper, nickel and zinc ions. Can you use data on heat of vaporization, ionization energy and enthalpy of solvation to determine what factors are responsible for the order of ease of oxidation of these metals?
Problem RO5.3.
Born Haber cycles are another example of thermodynamic cycles based on Hess' Law. These particular constructions are used to calculate the lattice energy of an ionic solid: the amount of energy released when ions in the gas phase condense to form an ionic lattice. This quantity is not easily measured directly.
The alternative pathway taken in the Born Haber cycle imagines that the separate ions in the lattice are first formed from the individual elements. The heat of formation of the ionic solid from the elements is usually known (or easily found on the internet, Herr Born and Herr Haber's favourite tool for evening relaxation), as are other physical parameters such as enthalpy of sublimation, ionization energies, electron affinities and so on.
Construct diagrams for the Born Haber cycle and estimate the lattice energy in each of the following cases.
a) LiCl b) CaF2 c) HgO d) ZnS
Some useful data can be found below. Note that enthalpy is a state function, so enthalpy of sublimation is roughly equal to enthalpy of fusion plus enthalpy of vaporization.
| mp (°C) | bp (°C) | ΔHfus (kJ/mol) | ΔHvap (kJ/mol) | IE1 (kJ/mol) | IE2 (kJ/mol) | Eea1 (kJ/mol) | Eea2 (kJ/mol) | |
| lithium | 180 | 1330 | 3 | 136 | 520 | 7298 | -50 | - |
| calcium | 842 | 1484 | 9 | 155 | 590 | 1155 | - | - |
| zinc | 419 | 907 | 7 | 115 | 906 | 1733 | - | - |
| mercury | -39 | 356 | 2 | 59 | 1007 | 1810 | 85 | - |
| oxygen | -218 | -183 | 0.4 | 7 | 1314 | 3388 | -226 | 879 |
| fluorine | -219 | -188 | - | 7 | 1681 | 3374 | -347 | - |
| sulfur | 115 | 444 | 2 | 45 | 1000 | 2252 | -100 | 435 |
| chlorine | -101 | -34 | 6 | 20 | 1250 | 2298 | -368 | - |
Problem RO5.4.
Thermodynamic cycles such as the ones we have used here are commonly used to determine phitsical data in chemistry.
For example, Bond strengths are fundamental to chemistry, but how do we determine the strength of a bond? A recent example comes from workers at University of Minnesota (Kass, J. Org. Chem. 2016, 81, 9175-9179), who looked at a particular bond in phenylcyclopropane.

a) Draw a thermodynamic cycle in which the reaction above is replicated by these steps:
i) the phenylcyclopropane
ionizes to form a proton plus a phenylcyclopropane anion
ii) the
phenylcyclopropane anion gives up one electron
iii) the proton gains an
electron
b) To study step (i), they
introduced hydroxide ion and phenylcyclopropane into a mass spectrometer.
Show the equilibrium that would result.
c) They measured the forward (kf = 2.0 x 10-9 s-1) and reverse (kr = 1.9 x 10-11 s-1) rate constants. Estimate the equilibrium constant, Keq.
d) Calculate the free energy of this reaction using ΔG = -RTlnKeq.
e) The reaction in (b) can also be broken down into a thermodynamic cycle with:
i) the phenylcyclopropane ionizes to form a proton plus a
phenylcyclopropane anion.
iv) water ionizes to form a proton plus a hydroxide
ion.
Draw this cycle.
f) Free
energy of step (iv) is calculated from the gas phase acidity of water (ΔG =
383.7 kcal/mol). You already calculated the free energy of (b).
What is ΔG of
step (i)?
g) To study step (ii), they treated phenylcyclopropane anion with different neutral molecules and looked for the appearance of corresponding anions in the mass spectrometer, indicating electron transfer had occurred.
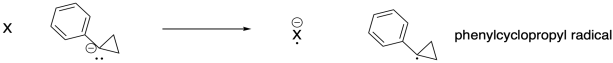
They obtained the following data:
|
Compd X |
Electron Affinity (eV) | Electron transfer? |
| SO2 | 1.107 | yes |
| C6F5Cl | 0.82 | yes |
| o-CF3C6H4CN | 0.70 | no |
| CS2 | 0.51 | no |
Estimate the electron affinity of phenylcyclopropyl radical.
h) That numerical value corresponds to the reduction potential of the phenylcyclopropyl radical in Volts. Calculate the free energy of this electron transfer using ΔG = - n F Eo. (n is the number of electrons transfered; F is the Faraday constant, 23 kcal V-1mol-1)
j) Step (iii) is a well-established quantity, the electron affinity of a proton, for which ΔG = -313.6 kcal/mol.
Calculate the bond dissociation energy of
phenylcyclopropane.
This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages. It is freely available for educational use.

Structure & Reactivity in Organic,
Biological and Inorganic Chemistry by
Chris Schaller
is licensed under a
Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
This material is based upon work supported by the National Science Foundation under Grant No. 1043566.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Navigation: