
Reactivity in Chemistry
Reduction & Oxidation Reactions
RO13. Solutions to Selected Problems
Problem RO1.1.
a) Ag+ b) Ni2+ c) Mn7+ d) Cr6+ e) Cu3+ f) Fe3+ g)Os8+ h) Re5+
Problem RO1.3.
a) Pb2+ & S2- b) Sn4+ & 2 O2- c) Hg2+ & S2- d) Fe4+ & 2 S2- e) 2 Fe3+ & 3 O2- f) 2 Fe3+ & 1 Fe2+ & 4 O2-
Problem RO1.4.
Probably Fe2+, to replace Zn2+ ions.
Problem RO1.5.
a) C 2+ b) C4+ c) 4- d) C0 e) C3+
Problem RO1.7.
a) Mg2+ b) Cu2+ c) Mn3+ d) Ca2+ e) Mn2+ f) Mn2+
Problem RO1.8.
a) Cu(II), Fe(II) b) Zn(II), Fe(III) c) Be(II), Al(III) d) Cu(I), Fe(III) e) Cu(II), Al(III)
Problem RO2.1.
a) Cu → Cu(+ + e-
b) Fe3+ + 3 e-→ Fe
c) Mn → Mn3+ + 3 e-
d) Zn2+ + 2 e- → Zn
e) 2 F- → F2 + 2 e-
f) H2 → 2 H+ + 2 e-
Problem RO2.2.
a) Cu(I) + Fe(III) → Cu(II) + Fe(II)
b) Cu(I) + Ag(0) → Cu(0) + Ag(I)
c) 3 F2 + 2 Fe → 6 F- + 2 Fe(III)
d) 2 Mo3+ + 3 Mn → 2 Mo + 3 Mn2+
Problem RO2.3.
a) MnO2 + 2 H+ + 2 e- → Mn(OH)2
b) 2 NO + 2 e- + 2 H+ → N2O + H2O
c) HPO32- + 2 e- + 3 H+ → H2PO2- + H2O
d) Sn(OH)62- + 2 e- + 3 H+ → HSnO2- + 4 H2O
Problem RO2.4
a) yes b) no c) yes d) no e) yes f) yes g) yes h) no
Problem RO2.5.
a) Erxn = - 0.153 V - 0.33 V = - 0.483 V
b) No.
c)

d) The O2 is activated as an electrophile. Addition of an electron may become easier.
e) The reduction potential is 0.2 V more positive when the resulting superoxide ion is stabilised by binding a proton. A similar shift could occur when coordinated to copper.
f)
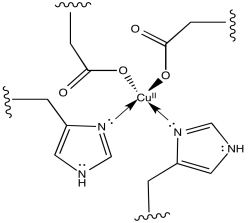
g) The two aspartate ions would make the copper complex less cationic. That may make it easier to remove an electron from the copper complex.
Problem RO2.6.
a) Fe2+ + ClO2 → Fe3+ + ClO2-
b) Erxn = 0.95 V - 0.77 V = 0.18 V
c) yes.
d)

e) ClO2 has an unpaired electron. ClO2- has electrons paired.
f) It could be inner sphere: the oxygen in the ClO2 could coordinate to the iron.
g) The mixture quickly forms (H2O)5Fe(ClO2)2+ via inner sphere electron transfer.
Problem RO3.1.
MnO4- : 4 x O2- (= 8-) + Mn7+ = 1- overall
MnO2 : 2 x O2- (= 4-) + Mn4+ = neutral overall
difference = 3 e-
Problem RO3.2.
a) SO42- : 4 x O2- (= 8-) + S6+ = 2- overall
S2O82- : 8 x O2- (= 16-) + 2 x S7+ (= 14+) = 2- overall
difference = 1 e- per S, or 2 e- overall
S2O82- + 2 e- → 2 SO42-
b) HPO32- : 3 x O2- (= 6-) + H+ + P3+ = 2- overall
P : P(0)
difference = 3 e-
HPO32- + 3 e- + 5 H+ → P + 3 H2O
c) Ti2O3 : 3 x O2- (= 6-) + 2 x Ti3+ (= 6+) = neutral overall
TiO : O2- + Ti2+ = neutral overall
difference = 1 e- per Ti, or 2 e- overall
Ti2O3 + 2 e- + 2 H+ → 2 TiO + H2O
d) N2 : N(0)
NH2OH : O2- + 3 x H+ (= 3+) + N- = neutral overall
difference = 1 e- per N, or 2 e- overall
N2 + 2 e- + 2 H+ + 2 H2O → 2 NH2OH
Problem RO3.3.
Lithium is an alkali metal, in the first column of the periodic table. It has a relatively low ionization energy because it has a noble gas configuration as a cation. That noble gas configuration is stable because of the relatively large number of nuclear protons and a relatively short distance between the nucleus and the outermost shell of electrons. In lithium metal, the outermost electron is relatively far from the nucleus and so it is at a relatively high energy, and easily lost.
Problem RO3.4.
Fluorine is a halogen, with a relatively high electron affinity. It easily gains an electron to get to a noble gas configuration as a fluoride anion. That noble gas configuration is stable because of the relatively large number of nuclear protons and a relatively short distance between the nucleus and the outermost shell of electrons.
Problem RO3.5.
From most easily oxidized to least easily oxidized: Li > Al > Fe > Cu > Au
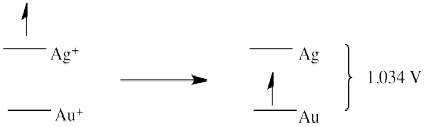
Problem RO3.6.
a) E0 = + 0.796 (Ag+/Ag) - 1.83 (Au/Au+) = -1.034 V (no forward reaction)
b) E0 = - 0.44 (Fe2+/Fe) + 0.762 (Zn/Zn2+) = + 0.0322 V (forward reaction)
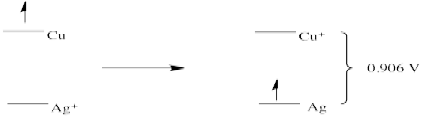
c) E0 = + 0.52 (Cu+/Cu) + 3.04 (Li/Li+) = + 3.56 V (forward reaction)
d) E0 = + 0.77 (Fe3+/Fe2+) - 0.796 (Ag/Ag+) = - 0.026 V (no forward reaction)
Problem RO3.7.
When the table of standard reduction potentials is displayed with the most negative value at the top and the most positive value at the bottom, any given half-reaction will go forward if it is coupled with the reverse of a half-reaction that lies above it in the table. The opposite is not the case; no half reaction will go forward if it is coupled with the reverse of a half-reaction below it in the table.
Problem RO4.1.
a)
 a
a
b)
c)

Problem RO4.2.
a) 2 Li + F2 → 2 Li+ + 2 F-
b) Eo = +5.91 V
c) Things look pretty grim.
d)
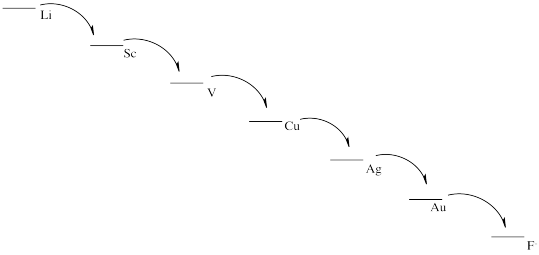
e) This scheme would result in the release of a small amount of energy at each stage. Each step could be harnessed to perform a task more efficiently, with less heat loss.
Problem RO4.3.
![]()
Problem RO4.4.
![]()
Problem RO4.5.
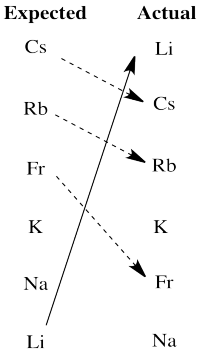
There are really two significant departures from expectation here. Lithium is much more active than expected based on electronegativity. The larger alkali metals, cesium, rubidium and francium, are all less active than expected on that basis.
We will see that another factor the influences activity in redox is the stability of ions in aqueous solution. Lithium cation is a small ion; water molecules bind very strongly to the ion because the electrons get relatively close to lithium's nucleus. That strong binding stabilizes this ion especially, tipping the malance of the reaction more strongly towards oxidation of lithium. The larger alkali metal ions are not nearly as stabilized by water ligands in aqueous solution, so the balance of their reactions does not tilt as strongly towards aqueous ions.
Problem RO5.1.
Li+/Li: E0 = - 3.04 V; ΔHvap = 147 kJ/mol; IE = 520 kJ/mol; ΔHh = -520 kJ/mol
Na+/Na: E0 = - 2.71 V; ΔHvap = 97 kJ/mol; IE = 495 kJ/mol; ΔHh = -406 kJ/mol
K+/K: E0 = - 2.931 V; ΔHvap = 77 kJ/mol; IE = 419 kJ/mol; ΔHh = -320 kJ/mol
Potassium should be the easiest of the three to oxidize. It is easier to oxidize than sodium. However, lithium's high heat of hydration reverses the trend and tips the balance of reaction in favour of ion formation.
Problem RO5.2.
Cu2+/Cu: E0 = + 0.340 V; ΔHvap = 300 kJ/mol; IE = 745 kJ/mol & 1958 kJ/mol; ΔHh = - 2099 kJ/mol
Ni2+/Ni: E0 = - 0.25 V; ΔHvap = 377 kJ/mol; IE = 737 kJ/mol & 1753 kJ/mol; ΔHh = - 2096 kJ/mol
Zn2+/Zn: E0 = - 0.7618 V; ΔHvap = 123 kJ/mol; IE = 906 kJ/mol & 1733 kJ/mol; ΔHh = - 2047 kJ/mol
In this case, zinc may be considered the outlier. Copper should be easier to reduce than nickel based solely on electronegativity. However, zinc's very low heat of vaporization suggests that formation of the solid metal is less favoured in that case, helping to tilt the balance toward zinc ion instead.
Problem RO5.3.
a)
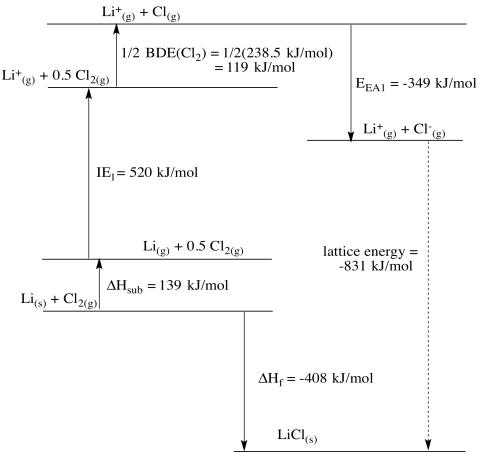
b)
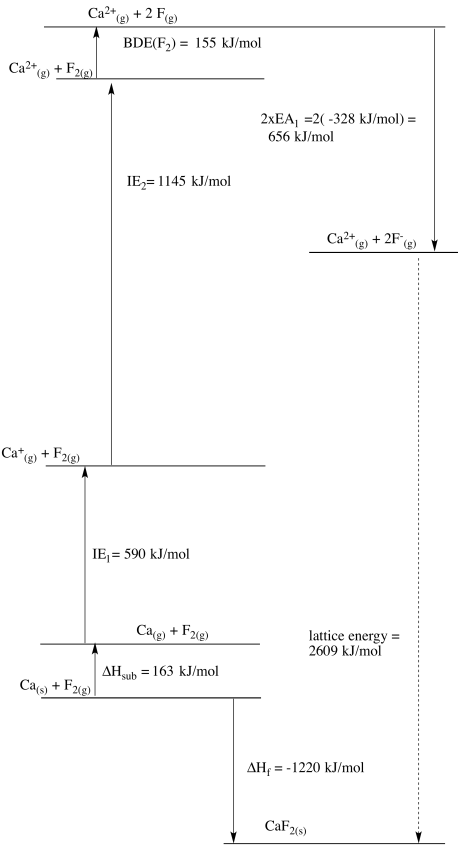
c)
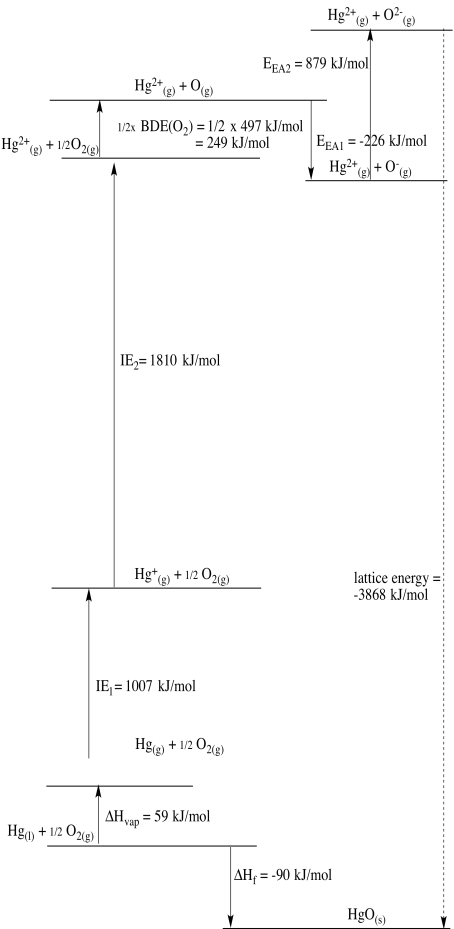
d)
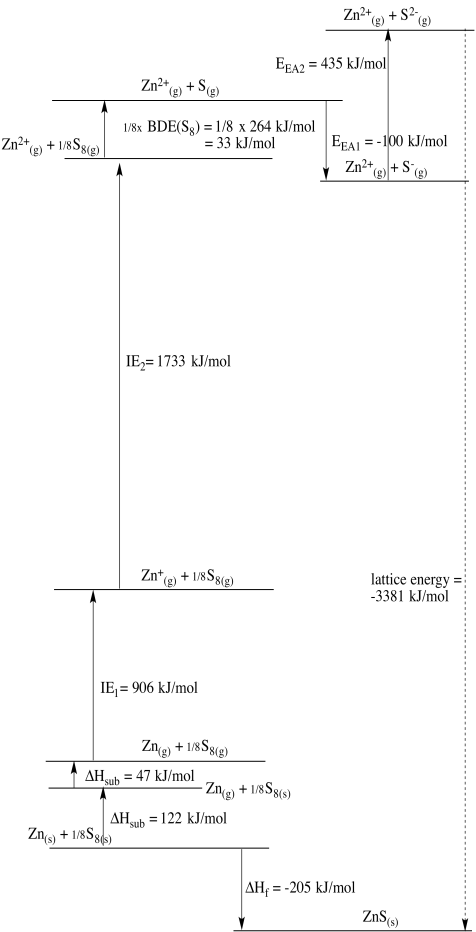
Problem RO5.4.
a)

b)

c) Keq = kf / kr = (2.0 x 10-9 s-1) / (1.9 x 10-11 s-1) = 105
d) Δg = - RTlnK = - (1.987 x 10-3 kcal K-1mol-1(298 K)[ln(105)] = -17.5 kcal/mol
e)
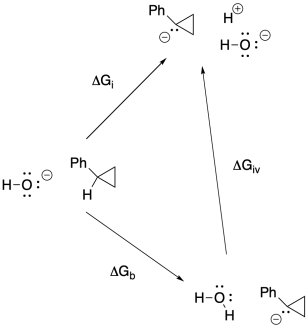
f)
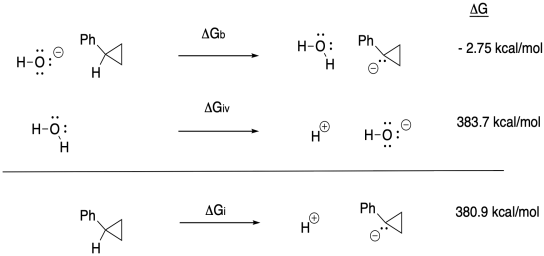
g) Anywhere between 0.70 eV and 0.82 eV, or 0.76 eV as an average.
h) ΔG = - nFEo = - (1)(23 kcal V-1 mol-1)(0.76 V) = -17.5 kcal // mol
(would be + 17.5 kcal/mol in the other direction)
j)
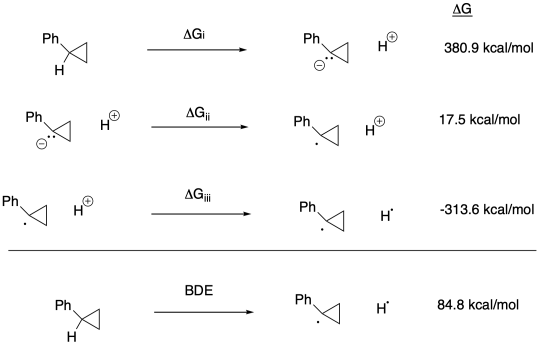
Problem RO6.1.
Both reduction potentials are very positive.
Ag+ + e- → Ag (s) E0 = + 0.796 V
Au+ + e- → Au (s) E0 = + 1.83 V
That means both metals are likely to be found in the reduced state.
Problem RO6.2.
SnO (s) + 2H+ + 2 e- → Sn (s) + H2O E0 = -0.10 V
CO(g) + H2O → CO2(g) + 2H+ + 2 e- E0 = - (-0.11 V)
SnO (s) + CO (g) → Sn (s) + CO2 (g) ΔE0 = + 0.01 V
Problem RO6.3.
Fe3O4(s) + 8 H+ + 8 e- → 3Fe(s) + 4 H2O E0 = +0.085 V
CO(g) + H2O → CO2(g) + 2H+ + 2 e- E0 = - (-0.11 V)
Fe3O4(s) + 4CO (g) → 3Fe(s) + 4CO2 (g) ΔE0 = + 0.195 V
Problem RO6.4.
Al3+(aq) + 3e- → Al (s) E0 = -1.662 V
CO(g) + H2O → CO2(g) + 2H+ + 2 e- E0 = - (-0.11 V)
2 Al3+(aq) + 3CO (g) + 3H2O → 2Al(s) + 3CO2 (g) ΔE0 = - 1.772 V
Problem RO6.5.
Al3+ + 3e- → Al (s) E0 = -1.662 V
2 O2- → O2(g) + 4e- E0 = - (.40 V, estimated)
4 Al3+(aq) + 6 O2- (aq) → 4 Al (s) + 3O2 (g) ΔE0 = - 2.062 V
Problem RO6.6.
Even if the aluminum ions from the cryolite are reduced to Al0, they will be replenished by new aluminum ions from the bauxite ore.
Problem RO7.1.
a) The potential of the zinc reaction is too negative to be spontaneous, so the zinc must be oxidized.
Zn(s) + 2OH- → ZnO(s) + H2O(l) + 2e- Eo = + 1.28 V
2 MnO2(s) + H2O(l) + 2e- → Mn2O3(s) + 2OH-(aq) Eo = + 0.15 V
The net reaction is:
2 MnO2(s) + Zn(s) → ZnO(s) + Mn2O3(s) Eo = + 1.43 V
b) This reaction involves a pair of electrons.
ΔG = - n F E0cell
ΔG = - 2 x 96,485 J V-1 mol-1 x 1.43 V
ΔG = - 275,947 J mol-1 = -276 kJ mol-1
Problem RO7.2.
a) We are told that citric acid gives up protons that form hydrogen gas. The protons are getting reduced.
2 H+ + 2 e- → H2(g) Eo = 0.0 V
That leaves either the copper or the zinc to be oxidized.
Zn2+ + 2e- → Zn(s) Eo = - 0.762 V
Cu2+ + 2e- → Cu(s) Eo = + 0.34 V
The oxidation of zinc would be spontaneous, but the oxidation of copper would not. The zinc is oxidized.
Zn(s) → Zn2+ + 2e- Eo = + 0.762 V
2 H+ + 2 e- → H2(g) Eo = 0.0 V
2 H+ + Zn(s) → Zn2+ + H2(g) Eo = + 0.762 V
b) This reaction involves a pair of electrons.
ΔG = - n F E0cell
ΔG = - 2 x 96,485 J V-1 mol-1 x 0.762 V
ΔG = - 147,043 J mol-1 = -147 kJ mol-1
Problem RO7.3.
a) The reactions are:
oxidation: Pb → Pb2+ + 2 e-
reduction: PbO2 + 4 H+ + 2 e- → Pb2+ + 2 H2O
b) The reactions are:
oxidation: Cd → Cd2+ + 2 e-
reduction: NiO(OH) + 3 H+ + 3 e- → Ni + 1.5 H2O
c) The reactions are:
oxidation: Zn → Zn2+ + 2 e-
reduction: MnO2 + H+ + e- → MnO2H
To learn about balancing reactions, see here.
Problem RO7.4.
a) The reactions are:
Ag2O (s) + H2O + 2 e- → 2 Ag (s) + 2 -OH (aq) E0 = +0.342 V
Zn (s) → Zn2+ (aq) + 2e- E0 = -(-0.762 V)
Ag2O (s) + H2O + Zn (s) → 2 Ag (s) + 2 -OH (aq) + Zn2+ (aq) ΔE0 = +1.104 V
b) Zn | Zn2+, HO- || HO- | Ag | Ag2O
Note the presence of the "extra" vertical line because hydroxide is in solution in the electrolyte but the silver metal would be a solid, in contrast to the zinc ion that is in solution with the hydroxide.
Problem RO7.5.
a) Charge on complex is calculated as follows:
charge on metal: 3+
charge on ligand donors (4 neutral N, 2 anionic N donors): 2-
other charges on ligand (carboxylate arm): 1-
overall: 0
b) ΔG = RT log K = RT (-pKa) = - 8.314 J K-1 mol-1 x 300 K x (-20.2) = 50,382 J mol-1 = 50.4 kJ/mol
c) It is more difficult to add the electron to the more negatively charged anion, so the reduction potential is more negative in that case.
d) ΔG = -n F E° = - 1 x 96,485 J V-1 mol-1 x (-0.545 V) = 52,583 J mol-1 = 52.6 kJ/mol
e) ΔG = -n F E� = - 1 x 96,485 J V-1 mol-1 x (-0.575 V) = 55,479 J mol-1 = 55.5 kJ/mol
f)
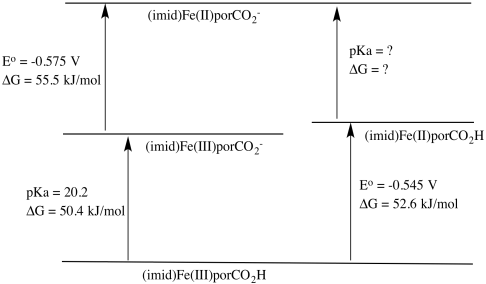
ΔGFe(II)CO2H/CO2- = 50.4 + 55.5 -52.6 kJ mol-1 = 53.3 kJ/mol
ΔG = -RT logKa
Ka = e(-ΔG/RT) = e((-53,300/(8.314 J /K mol x 300 K)) = e-21.4
pKa = 21.4
g) The Fe(III) complex is easier to deprotonate because it yields an anionic species, whereas the Fe(II) complex yields a dianionic species. The greater charge buildup in the latter would cost more energy.
Problem RO8.1.
a) Cu --> Cu2O MoO2 --> Mo
2 Cu --> Cu2O MoO2 --> Mo
2 Cu + H2O --> Cu2O MoO2 --> Mo + 2 H2O
2 Cu + H2O --> Cu2O + 2 H+ 4H+ + MoO2 --> Mo + 2 H2O
2 Cu + H2O --> Cu2O + 2 H+ + 2e- 4e- + 4H+ + MoO2 --> Mo + 2 H2O
2x (2 Cu + H2O --> Cu2O + 2 H+ + 2e- ) 4e- + 4H+ + MoO2 --> Mo + 2 H2O
adding:
4 Cu + 2 H2O --> 2 Cu2O + 4 H+ + 4e-
4e- + 4H+ + MoO2 --> Mo + 2 H2O
equals
4 Cu + MoO2 --> 2 Cu2O + Mo
b) NH2OH --> N2 Ag2O --> Ag
2 NH2OH --> N2 Ag2O --> 2 Ag
2 NH2OH --> N2 + 2 H2O Ag2O --> 2 Ag + H2O
2 NH2OH --> N2 + 2 H2O + 2 H+ 2 H+ + Ag2O --> 2 Ag + H2O
2 NH2OH --> N2 + 2 H2O + 2 H+ + 2 e- 2 H+ + Ag2O + 2 e- --> 2 Ag + H2O
adding:
2 NH2OH --> N2 + 2 H2O + 2 H+ + 2 e-
2 H+ + Ag2O + 2 e- --> 2 Ag + H2O
equals
2 NH2OH + Ag2O --> N2 + 2 Ag + 3 H2O
c) Fe3O4 --> Fe CO --> CO2
Fe3O4 --> 3 Fe CO --> CO2
Fe3O4 --> 3 Fe + 4 H2O H2O + CO --> CO2
8 H+ + Fe3O4 --> 3 Fe + 4 H2O H2O + CO --> CO2 + 2 H+
8 e- + 8 H+ + Fe3O4 --> 3 Fe + 4 H2O H2O + CO --> CO2 + 2 H+ + 2 e-
8 e- + 8 H+ + Fe3O4 --> 3 Fe + 4 H2O 4x (H2O + CO --> CO2 + 2 H+ + 2 e- )
adding:
8 e- + 8 H+ + Fe3O4 --> 3 Fe + 4 H2O
4 H2O + 4 CO --> 4 CO2 + 8 H+ + 8 e-
equals
Fe3O4 + 4 CO --> 3 Fe + 4 CO2
d) I2 --> IO3- MnO4- --> MnO2
I2 --> 2 IO3- MnO4- --> MnO2
6 H2O + I2 --> 2 IO3- MnO4- --> MnO2 + 2 H2O
6 H2O + I2 --> 2 IO3- + 12 H+ 4H+ + MnO4- --> MnO2 + 2 H2O
6 H2O + I2 --> 2 IO3- + 12 H+ + 10 e- 3 e- + 4H+ + MnO4- --> MnO2 + 2 H2O
3x (6 H2O + I2 --> 2 IO3- + 12 H+ + 10 e-) 10x ( 3 e- + 4H+ + MnO4- --> MnO2 + 2 H2O)
adding
18 H2O + 3 I2 --> 6 IO3- + 36 H+ + 30 e-
30 e- + 40 H+ + 10 MnO4- --> 10 MnO2 + 20 H2O
equals
3 I2 + 4 H+ + 10 MnO4- --> 6 IO3- + 10 MnO2 + 2 H2O
e) H3Mo7O24 --> Mo S2O32- --> SO32-
H3Mo7O24 --> 7 Mo S2O32- --> 2 SO32-
H3Mo7O24 --> 7 Mo + 24 H2O 3H2O + S2O32- --> 2 SO32-
45 H+ + H3Mo7O24 --> 7 Mo + 24 H2O 3H2O + S2O32- --> 2 SO32- + 6 H+
45 e- + 45 H+ + H3Mo7O24 --> 7 Mo + 24 H2O 3H2O + S2O32- --> 2 SO32- + 6 H+ + 4 e-
4 x (45 e- + 21 H+ + H3Mo7O24 --> 7 Mo + 24 H2O) 45 x (3H2O + S2O32- --> 2 SO32- + 6 H+ + 4 e- )
adding:
180 e- + 180 H+ + 4 H3Mo7O24 --> 28 Mo + 96 H2O
135 H2O + 45 S2O32- --> 90 SO32- + 270 H+ + 180 e-
equals
4 H3Mo7O24 + 45 S2O32- + 39 H2O --> 28 Mo + 90 SO32- + 90 H+
checking:
28 Mo --> 28 Mo; 90 S --> 90 S; 90 H --> 90 H; 270 O --> 270 O
Problem RO8.2.
a) Fe(OH)2 --> Fe2O3 N2H4 --> NH4+
2 Fe(OH)2 --> Fe2O3 N2H4 --> 2 NH4+
2 Fe(OH)2 --> Fe2O3 + H2O N2H4 --> 2 NH4+
2 Fe(OH)2 --> Fe2O3 + H2O + 2 H+ 4 H+ + N2H4 --> 2 NH4+
2 Fe(OH)2 --> Fe2O3 + H2O + 2 H+ + 2 e- 2 e- + 4 H+ + N2H4 --> 2 NH4+
adding:
2 Fe(OH)2 --> Fe2O3 + H2O + 2 H+ + 2 e-
2 e- + 4 H+ + N2H4 --> 2 NH4+
equals:
2 Fe(OH)2 + 2 H+ + N2H4 --> Fe2O3 + H2O + 2 NH4+
in basic conditions:
2 Fe(OH)2 + 2 H+ + 2 -OH + N2H4 --> Fe2O3 + H2O + 2 NH4+ + 2 -OH
2 Fe(OH)2 + 2 H2O + N2H4 --> Fe2O3 + H2O + 2 NH4+ + 2 -OH
2 Fe(OH)2 + H2O + N2H4 --> Fe2O3 + 2 NH4+ + 2 -OH
b) MnO4- --> HMnO4- V3+ --> VO2+
MnO4- --> HMnO4- V3+ + H2O --> VO2+
H+ + MnO4- --> HMnO4- V3+ + H2O --> VO2+ + 2 H+
e- + H+ + MnO4- --> HMnO4- V3+ + H2O --> VO2+ + 2 H+ + e-
adding:
e- + H+ + MnO4- --> HMnO4-
V3+ + H2O --> VO2+ + 2 H+ + e-
equals:
MnO4- + V3+ + H2O --> HMnO4- + VO2+ + H+
under basic conditions:
MnO4- + V3+ + H2O + -OH --> HMnO4- + VO2+ + H+ + -OH
MnO4- + V3+ + H2O + -OH --> HMnO4- + VO2+ + H2O
MnO4- + V3+ + -OH --> HMnO4- + VO2+
Problem RO9.1.
The bonds to iron would contract because the increased charge on the iron would attract the ligand donor electrons more strongly. The bonds to copper would lengthen because of the lower charge on the copper.
Problem RO9.2.
a) Most likely there are repulsive forces between ligands if the bonds get too short.
b) Insufficient overlap between metal and ligand orbitals would weaken the bond and raise the energy.
c) The range of possible bond lengths gets broader as energy is increased. The bond has more latitude, with both longer and shorter bonds allowed at higher energy.
Problem RO9.3.
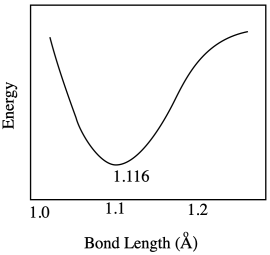
Problem RO9.4.
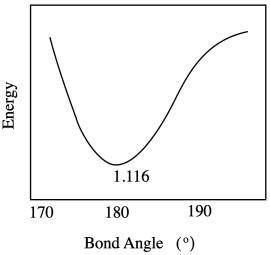
Problem RO9.5.
The water molecules may pivot toward the more highly charged Fe(III), or they may shift closer to it because of the attraction between the ion and the dipole of the water molecule.
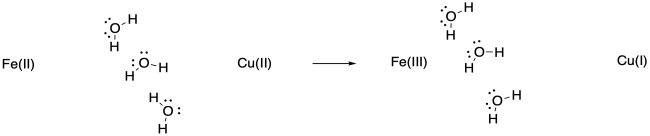
Keep in mind that such adjustments would happen in non-polar solvents, too, although they would involve weaker IMFs such as ion - induced dipole interactions.
Problem RO9.6.
The reactants and products are very similar in this case. However, the Fe(III) complex has shorter bonds than the Fe(II) complex because of greater electrostatic interaction between the metal ion and the ligands. These changes in bond length needed in order to get ready to change from Fe(III) to Fe(II) (or the reverse) pose a major barrier to the reaction.
Problem RO9.7
a) The drawing is an oversimplification, but in general the water molecules are shown reorienting after the electron transfer because of ion-dipole interactions. In this case, the waters are shown orienting to present their negative ends to the more positive iron atom after the electron transfer. In reality, in a protein there are lots of other charges (including charges on the ligand) that may take part in additional ion-dipole interactions.
b) Because electron transfer is so fast, atomic and molecular reorganisations are actually thought to happen before the electron transfer. The water molecules would happen to shift into a position that would provide the greatest possible stabilisation for the ions and then the electron would be transferred. A less polar solvent than water would be less able to stabilize ions and the electron would be slower to transfer as a result. In addition, a less polar solvent than water would be a poor medium to transmit an electron, which is charged and therefore stabilized by interactions with polar solvents.
Problem RO9.8.
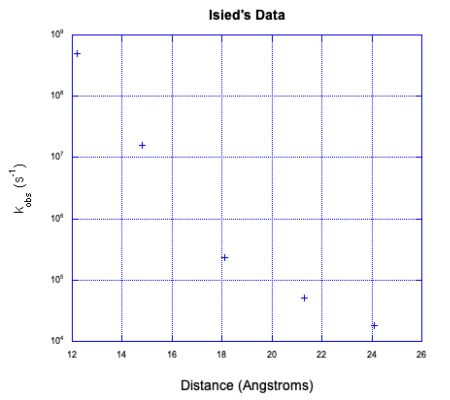
a) Here is a plot of the data.
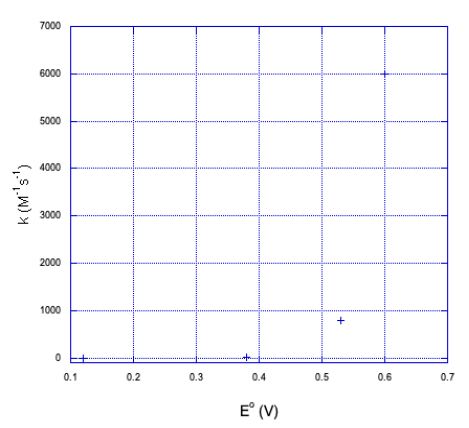
b) It doesn't look linear. If we plot the y axis on a log scale, things become a little more linear.
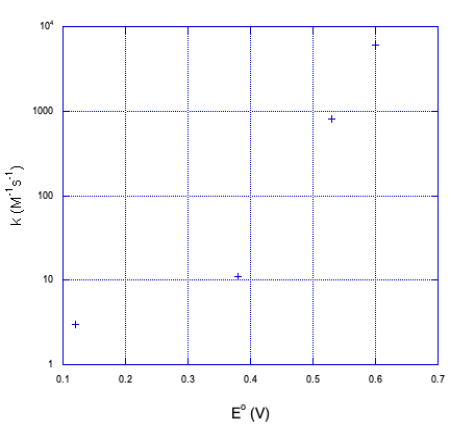
It looks closer to a logarithmic relationship than a linear one.
c) Assuming one electron transfer:
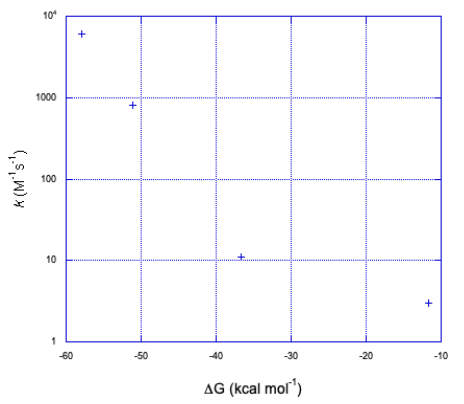
The graph takes the same form but in the opposite direction along the x axis.
Problem RO9.9.
a)
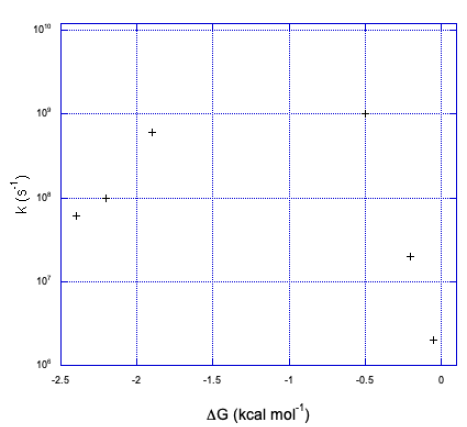
b) We can see two sides of an inverted curve. The reaction gets much faster as the free energy becomes more negative, but at some point the rate begins to decrease again.
Problem RO9.10.
The acceptor compound becomes an anion when it accepts an electron. The first three compounds do not appear to be strongly electrophilic; they can accept electrons simply because of resonance stability of the resulting anion. The last three have electron withdrawing groups (chlorines and oxygens) that would stabilize the anion even further.
Problem RO9.11.
a) octahedral; bpy is a bidentate ligand.
b) Co is first row; Co(I) and Co(II) have relatively low charge. Usually we would expect them to be high spin. Co(III) is at a cut-off point in the first row; it is just electronegative enough that isit is udually low spin.
c)
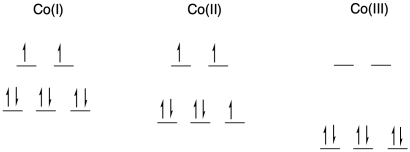
d) In a transfer from Co(II) to Co(III), there is additional reorganization needed because the metal changes between high and low spin. Not only does one electron have to move from one metal to another metal, but additional electrons have to shuffle from one orbital to another on the same metal to accommodate the change. These reorganizations have a barrier, slowing the reaction.

Problem RO10.1.
a) octahedral
b) In the first row, 2+ complexes are almost always high spin. However, 3+ complexes are sometimes low spin.
c)
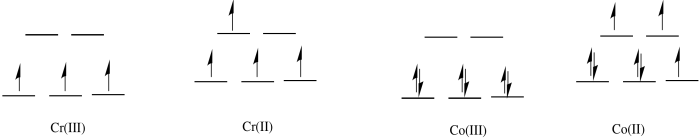
d) The Co(II) complex is high spin and labile. The ligands are easily replaced by water.
e) The Cr(III) complex is only d3; it is inert.
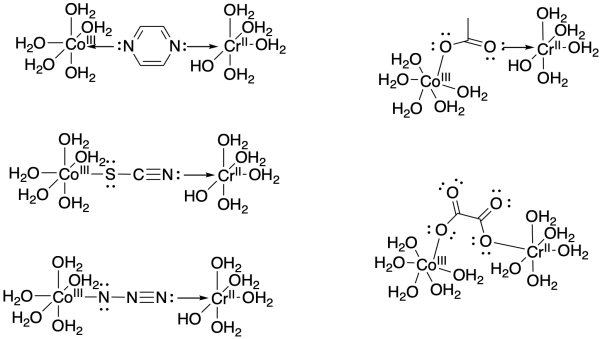
Problem RO10.2.
Problem RO10.3.
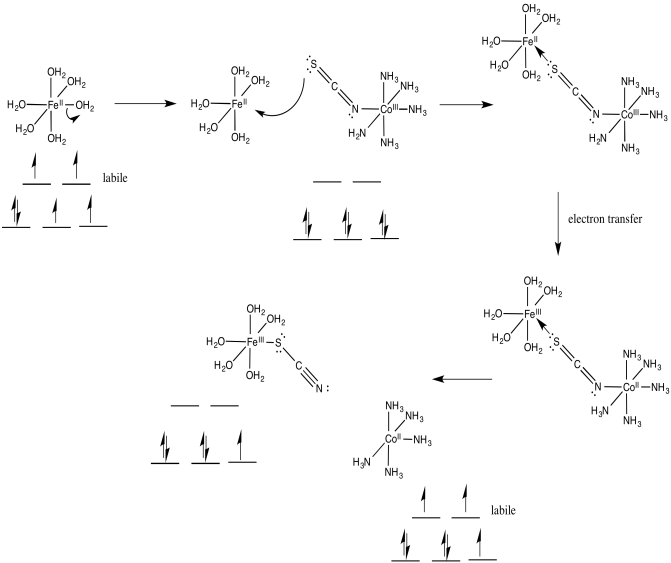
Problem RO10.4.
a)
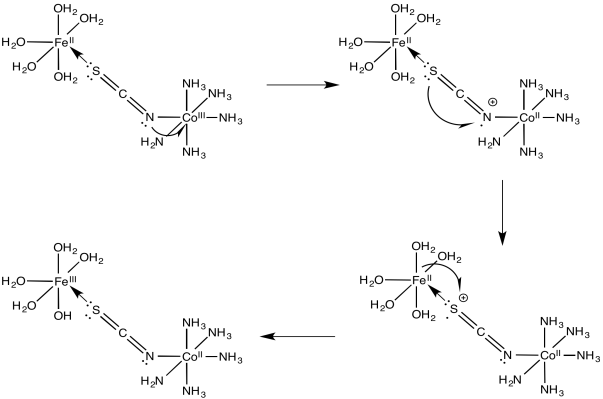
b)
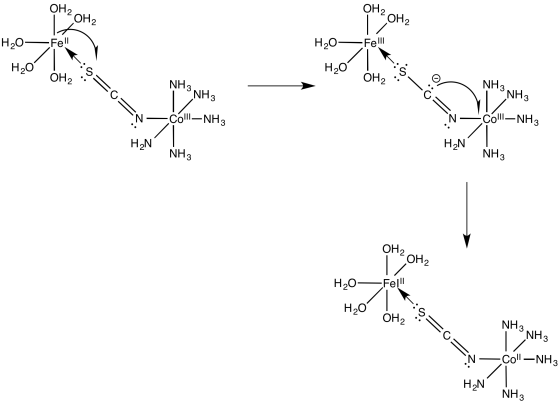
Problem RO10.5.
a)
b) The electron transfer between Os(II) and Ru(III) will not involve any electron reorganization because both are low spin to begin with. However, the electron transfer between Os(II) and Co(III) will result in cobalt changing from low spin to high spin. The need to move electrons between different d orbitals on the cobalt will add to the barrier, slowing down the reaction.
c) The pathway is probably inner sphere because of the bridging ligand. Furthermore, the conjugation in the bridging ligand would help in conducting an electron from one end of the ligand to the other, either through an electron mechanism or a hole mechanism.
Problem RO10.6.
a) The rate decreases exponentially as distance increases.
b) You might keep the concentration low in order to increase the distance between molecules, reducing the likely hood of an outer-sphere electron transfer.
c) If you ran the experiment at a series of dilutions, intramolecular electron transfer would be unaffected but outer sphere electron transfer would not. If the rates were the same across a number of different concentrations, the reaction would probably be intramolecular.
Problem RO10.7.
a) Rings are frequently used to introduce conformational rigidity (or decrease conformational flexibility), limiting the range of potential shapes a molecule could adopt. If the molecule can't wiggle around as much, then the distance between the ends of the molecule should be more constant.
b) Although the ligand is bridging, it would be difficult to picture either an electron or hole mechanism of inner sphere electron transfer. There are few pi bonds or lone pairs to use as places to put electrons or temporarily remove electrons from, shuttling the electrons from place to place along the ligand. A conjugated system would be much more likely to carry out inner sphere electron transfer.
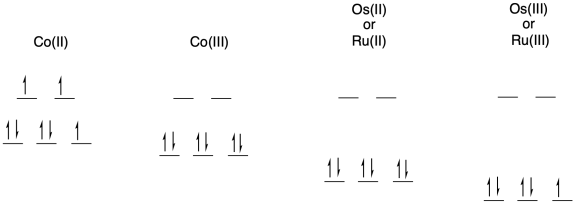
c)
d) The data is not linear.
e) The data appear to show two lines that cross. That's a classic symptom of two competing mechanisms. The faster mechanism, to the left, is probably an intramolecular electron transfer. The slower mechanism, to the right, may be an intermolecular electron transfer.
Problem RO1.8.
a)
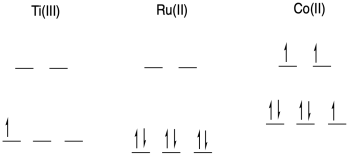
b) With an open t2g level, Ti(III) is associatively labile.
With a filled t2g level and empty eg level, Ru(II) is inert to substitution.
With an occupied eg level, Co(II) is dissociatively labile.
c) Outer sphere. Ruthenium lacks a bridging ligand, so it would have to be supplied by Co. Even if Co had such a ligand, it would be unable to bind to the ruthenium until another ligand left, which is unlikely as the ruthenium is inert.
d) The ones that fall on the line undergo the same mechanism. Since ruthenium undergoes outer sphere electron transfer, the titanium complexes along this line also undergo OSET.
e) These points are above the line, so they represent cases that are much faster with titanium compared to what is expected by looking at ruthenium.
f) These last one smust undergo inner sphere electron transfer. ISET would be possible with titanium, as it could easily bind a bridging ligand provided by the cobalt.
Problem RO11.1.
The compound undergoes a two-electron oxidation. The oxidized species then undergoes a two-electron reduction.
Problem RO12.2.
a) CH2CHCH3
| C-H bonds | 6- |
| C-X bonds | 0 |
| Oxidation Level | 6- |
CH3CH2CH3
| C-H bonds | 8- |
| C-X bonds | 0 |
| Oxidation Level | 8- |
Propane results from a two-electron reduction of propene.
b) CH3CH2CHO
| C-H bonds | 6- |
| C-X bonds | 2+ |
| Oxidation Level | 4- |
CH3CH2CH2OH
| C-H bonds | 7- |
| C-X bonds | 1_ |
| Oxidation Level | 6- |
Propanol results from a two-electron reduction of propanal.
c) CH3CH(OH)CH2CH2OH
| C-H bonds | 8- |
| C-X bonds | 2+ |
| Oxidation Level | 6- |
CH3COCH2CHO
| C-H bonds | 6- |
| C-X bonds | 4+ |
| Oxidation Level | 2- |
3-oxobutanal results from a four-electron oxidation of 1,3-butanediol.
Problem RO12.4.
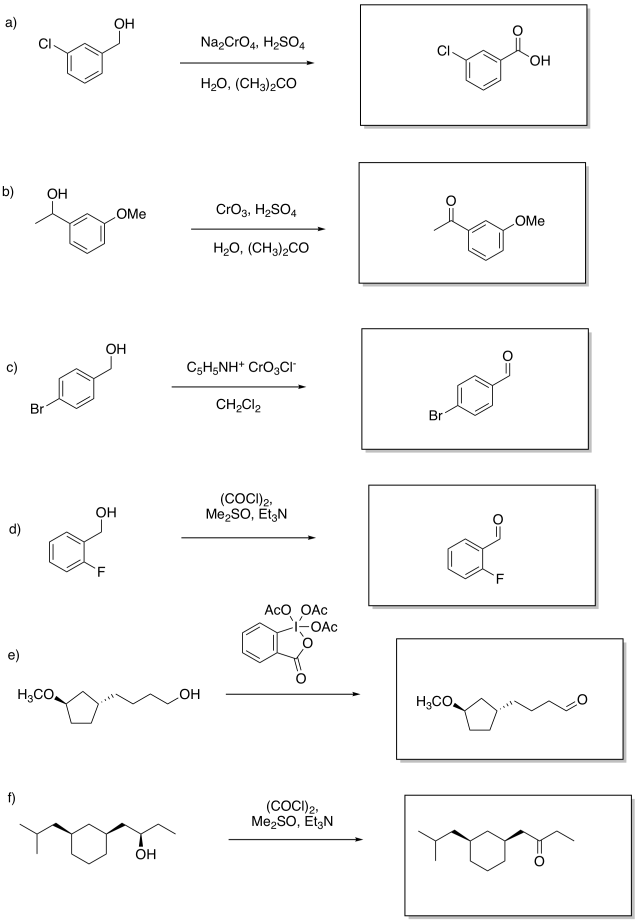
Problem RO12.5.
Multiple answers may be possible. However, (a) and (e) require aqueous oxidizing conditions whereas (b) excludes aqueous oxidizing conditions.
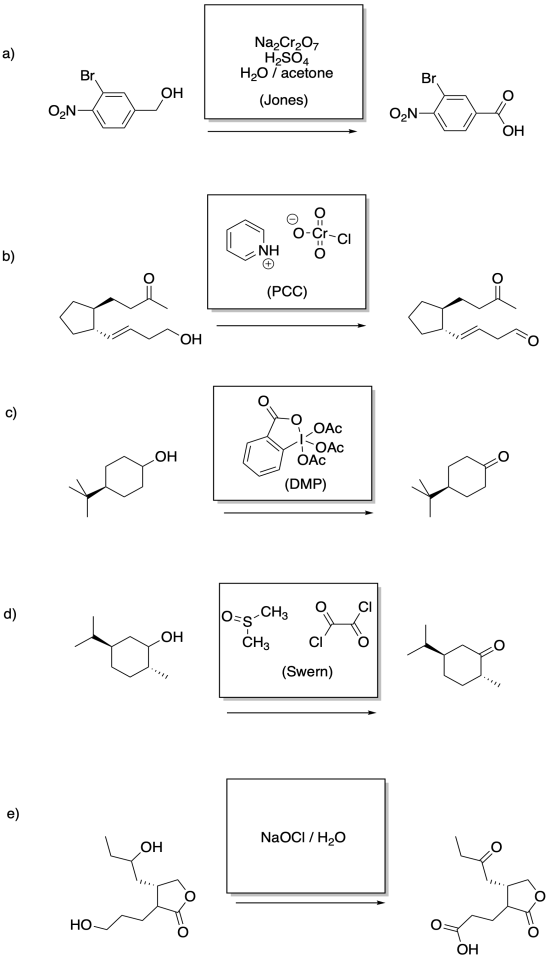
Problem RO12.6.
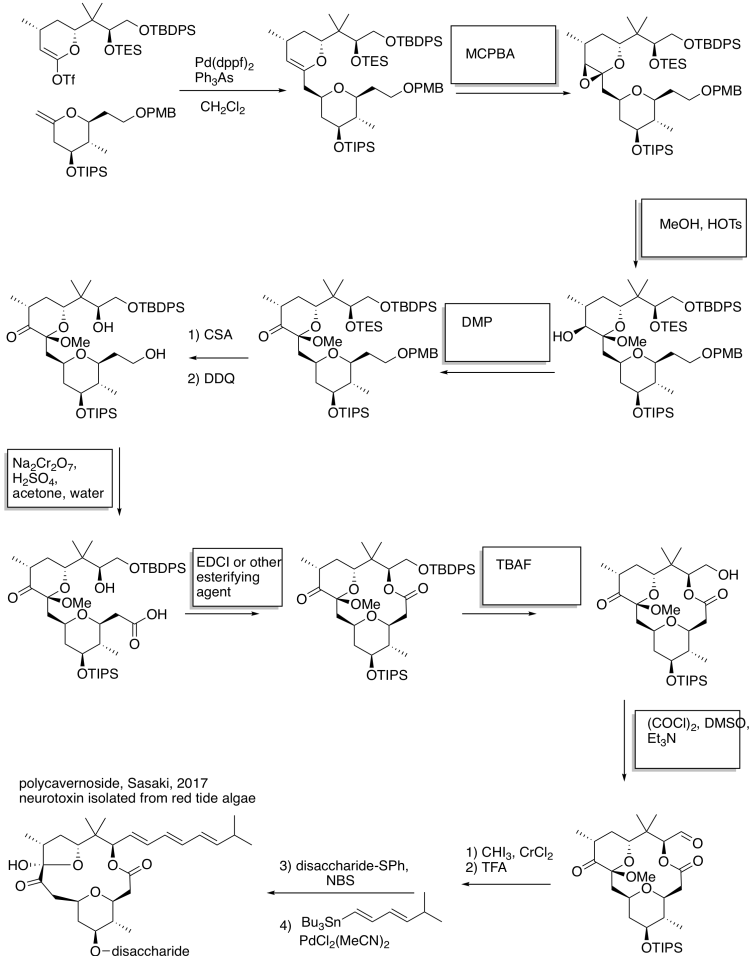
Problem RO12.7.

This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages. It is freely available for educational use.

Structure & Reactivity in Organic,
Biological and Inorganic Chemistry by
Chris Schaller
is licensed under a
Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
This material is based upon work supported by the National Science Foundation under Grant No. 1043566.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Navigation: