Reaction Rates and Equilbrium
As we have studied chemical reactions, we have learned
For the most part, we have also assumed that reactions occur in only one direction, that is, from reactant to product. We did mention, however, that in acid/base reactions, and for redox reactions, the reactions are hypothetically reversible, but prefer to go in the direction of strong to weak acid/base or oxidizing/reducing agent. Now we would like to expand our discussion of reactions to consider reactions that are readily reversible. We would like to know three additional features of any reaction:
As we will see the first two are closely related. Energy changes are extremely important to a world that has great energy needs to drives its technological civilization.
Reversible/Irreversible Reactions, Extent of Reactions, Equilibrium: Consider a hypothetical reversible reaction in which you start with some reactants, A and B, each at a 1 M concentration (1 mol of each/L solution). but no products, P and Q. For ease assume that the total volume of solution is 1 L, so that we start with 1 mol each of A and B.. At time t=0, the concentration of products is 0. The reaction can be written as:
As time progresses, the amounts or concentrations of A and B decrease as the amounts or concentrations of products P and Q increase. At some time, no further changes occur in the amount or concentrations of remaining reactants or products. At this point the reaction is in equilibrium, a term used often in our common vocabulary to denote a system that isn't changing.).
Most of the reactions that we will study occur in solution, so we will deal with concentrations (in mol/L or mmol/mL = M Lets consider how the concentration of reactants and products change as a function of time. Depending on the extent to which a reaction is reversible, 4 different scenarios can be imaged:
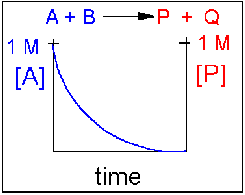
Scenario 1: Irreversible reaction in which the reverse reaction occurs to a negligible extent.
In this reaction, the reverse reaction occurs to such a small extent that we can neglect it. The only reaction that occurs is the conversion of reactants to product. Hence all the reactants are converted to product. At equilibrium [A] = 0. Since 1 mol of A reacted, it must form 1 mol of P and 1 mol Q - i.e. the concentration of products at equilibrium is 1 M. At an earlier time of the reaction, (let's pick a time when [A] = 0.8 M), only part of the reactants have reacted (in this case 0.2 M), producing an equal amount of products, P and Q. Graphs of [A] and [P] as a function of timer are shown below. A decreases in a nonlinear fashion to 0 M while P increases in a reciprocal fashion to 1 M concentration. This is illustrated in the graph below.

Examples of irreversible reactions are reactions of strong acids (like nitric, sulfuric, hydrochloric) with bases like OH- and water, or combustion reactions like the burning of sugars (like trees) and hydrocarbons (like octane) to form CO2 and H2O.
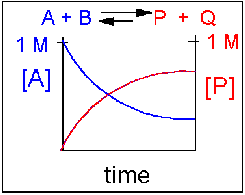
Scenario 2: Reversible reaction in which the forward reaction is favored.
Again [A] decreases and [P] increases, but in this case, some A remains since the reaction is reversible. As A and B decrease, P and Q increase, which increases the chance that they will collide and form product. Since P and Q can react to from reactants, the [A] at equilibriumis not zero as is show below.
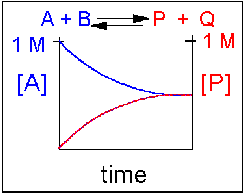
Scenario 3: Reversible Reaction in which forward and reverse reactions are equally favored.
Again [A] decreases and [P] increases, but in this case, some A remains since the reaction is reversible. As A and B decrease, P and Q increase, which increases the chance that they will collide and form product. Since P and Q can react to from reactants, the [A] at equilibrium is not zero as is show below. Because the reactants and products are equally favored, their concentration will be equal at equilibrium.
Scenario 4: Reversible Reaction in which the reverse reaction is favored.
Again [A] decreases and [P] increases, but in this case, some A remains since the reaction is reversible. As A and B decrease, P and Q increase, which increases the chance that they will collide and form product. Since P and Q can react to from reactants, the [A] at equilibrium is not zero as is show below. Because the reaction favors reactants. their concentration will be higher at equilibrium than the products.
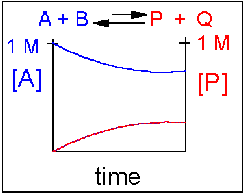
An example of this kind of reaction, one that favors reactants, is the reaction of acetic acid (a weak acid) with water.
Equilibrium Constants:
Without a lot of experience in chemistry, it is difficult to just look at the reactants and products and determine whether the reaction is irreversible, or reversible, favoring either reactants or products (with the exception of obvious irreversible reactions described above). However this data can be found in table of equilibrium constants found in reference books. Look at scenario 2 (a product favored reversible reaction). Consider A <--> P, where at t = 0, A = 1M and P=0M. At equilibrium, A might = 0.2 M implying that 0.8 mol/L A reacted forming 0.8 mol/L of P. 80% of A reacted. If initially A = 0.1 M, then at equilibrium, A = 0.02M and P = 0.08 M. Again, 80% of A reacted. The equilibrium constant, Keq, for this reaction is: Keq = [P]eq/[A]eq = 0.8/0.2 = 0.08/0.02 = 4. The equilibrium constant, as its name implies, is constant, independent of the concentration of the reactants and products. A Keq > 1 implies that the products are favored. A Keq < 1 implies that reactants are favored. When Keq = 1, both reactants and products are equally favored. For the more general reaction,
aA + bB <==> pP + qQ, where a, b, c, and d are the stoichimetric coefficients, Keq = ([P]p[Q]q)/([A]a[B]b). For a simple reaction where a, b, p, and q are all 1, then Keq = ([P][Q])/([A][B]).
For a irreversible reaction, such as the reaction of a 0.1 M HCl(aq) in water, [HCl]eq = 0, so you can't calculate a Keq. However, if we assume the reaction goes in reverse to an almost imperceptible degree, [HCl]eq might equal 10-10 M. Hence Keq >> 1.
In summary, the extend of reactions can vary from completely irreversible (favoring only the products) to reactions that favor the reactants . Our next goal is to understand what controls the extent of a reaction. Our answer will be energy changes. We will see example of these different types of reversible reactions later.
WCB Quiz - Equilibrium: Answers
Reactions and Energy Change
Why do reactions vary in extent form completely irreversible in the forward reaction to reversible reactions favoring the reactants? It might help to understand a simple physical reaction before we try more complicated chemical reactions.
Ball on a hill. Does a ball at the top of a hill roll downhill spontaneously, or does the opposite happen? No one has ever seen a ball roll spontaneously uphill unless a lot of energy was added to the ball. This physical reaction appears to be irreversible, and occurs because the ball has lower potential energy at the bottom of the hill than it does at the top. The gap in the potential energy is related to the "extent" and spontaneity of this reaction. As we have observed before, nature tends to go to a lower energy state.
ANIMATION: BALL ON A HILL - WHAT YOU ALWAYS SEE!
ANIMATION: BALL ON A HILL - WHAT YOU NEVER SEE!
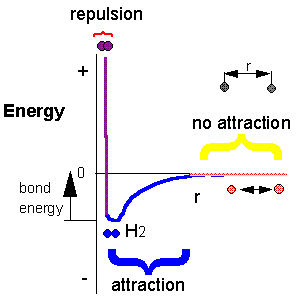
H + H --> H2 Does this reaction occur spontaneously? It does. You should remember that individual H atoms are unstable, since they don't have an completed outer shell of electrons - in this case a duet. As they approach, they can stability interact to form a covalent bond and in the process release energy. The bonded state is a lower energy state than two separated H atoms. This should be clear since energy has to be added to a molecule of H2 to break the bond.
2C8H18(l) + 25O2(g) --> 16CO2(g) + 18H2O(g). To carry out this reaction, every C-C, C-H and O-O bond in the reactants must be broken (which requires an input of energy) but a lots of energy is released on formation of C-O and H-O covalent bonds in the products. Is more energy needed to break the bonds in the reactants or is more energy released on formation of bonds in the product? The answer should be clear. The products must be at a lower energy than the reactants since huge amounts of heat and light energy are released on combustion of gasoline and other hydrocarbons.
These reactions suggests that energy must be released for a reaction to proceed to any extent in a given direction.
Now consider, however, the following reaction which I demonstrated in class:
Ba(OH)2.8H2O(s) + 2NH4SCN(s) --> 10H2O(l) + 2NH3(g) + Ba(SCN)2(aq+s)
When these two solids are mixed, and stirred, a reaction clearly takes places, as evidenced by the formation of a liquid (water) and the smell of ammonia. What is surprising is that heat is not released into the surroundings in this reaction. Rather heat was absorbed from the surroundings turning the beaker so cold that it froze to the piece of wood (with a layer of water added to the wood) on which it was placed. This reaction seems to violate our idea that a reaction proceeds in a direction in which heat is liberated. Reactions which liberate heat and raise the temperature of the surroundings are called exothermic reactions. Reactions which absorb heat from the surroundings and hence lower the temperature of the surroundings are endothermic reactions.
For exothermic reactions, the reactants have more energy than the products, and the heat energy (measured in kcalories) released is the difference between the energy of the products and reactants. When heat energy is used to measure the difference in energy, we call the energy enthalpy (H) and the heat released as the change in enthalpy (DH), as illustrated below.
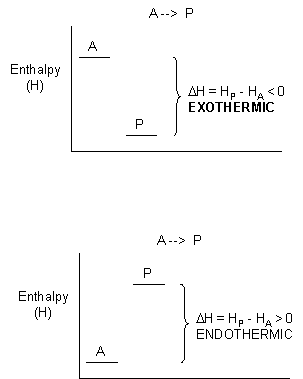
For exothermic reactions, ΔH < 0. For endothermic reactions, ΔH > 0.
Clearly, there must be something more that decides whether a reaction goes to a significant extent other that if heat is released. Another example of a spontaneous natural reaction is the evaporation of water (a physical, not chemical process).
Heat is absorbed from the surroundings to break the IMF's (H bonds) among the water molecules, allowing the liquid to be turned into a gas. If the surroundings are the skin, evaporation of water in the form of sweat cools the body. What are these reactions spontaneous and essentially irreversible even though they are endothermic? Notice that in both of these endothermic reactions, the products are more disorganized (more disordered) than the products. A solid is more ordered than a liquid or gas, and a liquid is more ordered than a gas. All our experiences with nature, from keeping your room clean or the evaporation of water, shows us that nature, ordered things become more disordered with time. Entropy (S) is a measure of the disorder of a system. The greater the entropy, the greater the disorder. All nature tends toward disorder. For reactions that go from order (low S) to disorder (high S), the changed in S, ΔS = SProducts - Sreactants > 0. For reaction that go from low order to high order, ΔS < 0.
Whether reactions are spontaneous in a given direction depends not just if the reaction is exothermic (since some reactions are endothermic) or just entropy (since some reactions that increase order occur spontaneously) but on some combination of both, as illustrated in the table below.
|
reaction |
Δenthalpy (ΔH) |
Δentropy (ΔS) |
favored/disfavored |
|
combustion of fuels |
exothermic (<0) |
positive (>0) |
always favored |
|
various |
exothermic (<0) |
negative(<0) |
depends |
|
endothermic (>0) |
positive (>0) |
depends |
|
|
synthesis of sugars from CO2 and H2O |
endothermic (>0) |
negative (<0) |
always disfavored |
WCB QUIZ: ΔG, ΔH, and ΔS. Answers
Contributions of Keq and concentration to DG
We have just seen that ΔG is a function of both enthalpy and entropy - reflecting the dual contributions to the total energy change of heat and order changes in the system. There are two other factors, more directly related to the actual chemistry of the system, that contribute to ΔG - the equilibrium constant, Keq, and the concentrations of reactants and products. Two examples - the reactions of hydrochloric acid and acetic acid - illustrate this point.
Assume that at t = 0, each acid is placed into water at a concentration of 0.1 M. When equilibrium is reached, there is essentially no HCl left in solution, while 99% of the acetic acid remains. Why are they so different? We rationalized that HCl(aq) is a much stronger acid than H3O+(aq) which itself is a much stronger acid than CH3CO2H(aq). Why? All we can say is there is something about the structure of these acids (and the bases) that makes HCl much more intrinsically unstable, much higher in energy, and hence much more reactive than the acid it forms, H3O+(aq). Likewise, H3O+(aq) is much more intrinsically unstable, much higher in energy, and hence more reactive than CH3CO2H(aq). This has nothing to do with concentration, since the initial concentration of both HCl(aq) and CH3CO2H(aq) were identical. This observation is reflected in the Keq for these acids (>>1 for HCl and <<1 for acetic acid). This difference in intrinsic stability of reactants compared to products (which is independent of concentration) is one factor that contributes to ΔG.
The other factor is concentration, as I demonstrated in class. A 0.25 M (0.25 mol/L or 0.25 mmol/ml) solution of acetic acid does not conduct electricity, implying that very few ions of H3O+(aq) + CH3CO2-(aq) exist in solution. However, as I added more concentrated acetic acid, a dim light was evident. Adding more reactant seemed to drive the reaction to form more products, even though the reverse reaction is favored if one considers only the intrinsic stability of reactants and products. Before the concentrated acid was added, the system was at equilibrium. Adding concentrated acid perturbed the equilibrium, which drove the reaction to form additional products. This is an example of Le Chatelier's Principle, which states that if a reaction at equilibrium is perturbed, the reaction will be driven in the direction that will relieve the perturbation. Hence:
These two factors more directly associated with the chemistry of the reaction, intrinsic reactivity of reactants compared to products (related to the Keq) and concentration, affect ΔG. Just as the relationship between ΔG could be expressed as the sum of the two contributions showing the effects of heat changes (enthalpy change) and entropy changes:
so can the relationship between ΔG be expressed as the sum of the two contributions showing the effects of the intrinsic stability and concentration:
where ΔGostab reflects the contribution from the relative intrinsic stability of reactants and products) and ΔGconc reflects the contribution from the relative concentrations of reactants and products (which has nothing to do with stability). Both equations are true. Both show that the total DG can be expressed as the sum of the two contributions- either changes in enthalpy and entropy, or relative stabilities and concentrations .
Meaning of ΔG
Remember that ΔG is the "driving" force for a reaction, analogous to the difference in potential energy for a ball on a hill. Go back to that analogy. if the ball starts at the top of the hill, does it roll down hill? Of course. It goes from high potential energy to low potential energy. The reaction can be written as: Balltop --> Ballbottom for which the change in potential energy, ΔPE = PEbottom -PEtop< 0. If the ball starts at the bottom, will it go to the top? Obviously not. For that reaction, Ballbottom --> Balltop, ΔPE > 0. If the top of the hill was at the same height at the bottom of the hill (obviously an absurd situation), the ball would not move. It would effectively be at equilibrium, a state of no change. For this reaction, Balltop --> Ballbottom, the ΔPE = 0. As the ball starts rolling down the hill, its potential energy gets closer to the potential it would have at the bottom. Hence the ΔPE changes from negative to more and more positive until it gets to the bottom at which case the ΔPE = 0 and movement ceases. If the ΔPE is not 0, the ball will move until the ΔPE = 0.
Likewise, for a chemical reaction that favors products, ΔG < 0. The system is not at equilibrium and the reaction will go in the direction of products. As the reaction proceeds, products build up, and there is less of a driving force for reactants to go to products (LeChatiliers Principle), so the ΔG becomes more a more positive until the ΔG = 0 and the reaction is at equilibrium. A reaction that has a ΔG > 0 is likewise not at equilibrium so it will go in the appropriate direction until equilibrium is reached. Hence for the reaction A + B <==> P + Q,
We can not measure easily the actual free energy G of reactants or products, but we can measure ΔG readily. These points are illustrated in the graph of ΔG vs time for the hypothetical reaction A + B <==> P + Q. (Also notice the two insert graphs - in blue and red - which show, in analogy to the ball on the hill graphs, the values of ΔG at the two points where the perturbation to the equilibrium were made.)

Notice the ΔG is constantly changing until the system reaches equilibrium. Initially the equilibrium is perturbed so that the system is not in equilibrium (shown in blue). The perturbation was such that the products are favored. After equilibrium was reached, the system was perturbed again, this time in a fashion to favor the reverse reaction. Notice in this case the ΔG for the reaction as written: A + B <==> P + Q is positive - i.e. it is not in a . Therefore the reaction (as written) goes backwards to products. It is important to realize that the reported ΔG is for the reaction as written.
Now let's apply ΔG = ΔGostab + ΔGconc to two reactions we discussed above:
Assume that at time t=0, 0.1 mole of HCl and CH3CO2H were added to two different beakers. At this point the forward reaction are favored, but obviously given to different extents. The ΔGconc would be identical for both acids, since each reactant is present at 0.1 M, but no products yet exist. However, the ΔGostab is much more negative for HCl than acetic acid since HCl is a strong acid. Hence at t=0, ΔG for the HCl reaction is much more negative than for acetic acid. This is summarized in table below. The direction of the arrow shows if products (-->) or reactants (<---) are favored. The size of the arrow shows very approximately to what extent the ΔG term is favored
Reaction at t=0 HCl(aq) +
H2O(l) ---------------> ---------------> -----------------------------> CH3CO2H(aq)
+ H2O(l) <------------- ---------------> ->
Now when equilibrium is reached, a state of no net changed in concentration of reactants and products, ΔG = 0. In the case of HCl, there is just an infinitessimal amount of HCl left, and 0.1 M of each product, so concentration favors its formation. However, the intrinsic relative stability of reactants and products still favors products. In the case of acetic acid, most of the acetic acid remains (0.099 M) with little product (0.001 M) so concentration favors product. However, the intrinsic relative stability of reactants and products still favors reactants. This is summarized in table below.
Reaction at equlib. HCl(aq) +
H2O(l) ---------------> <--------------- favors neither, =
0 CH3CO2H(aq)
+ H2O(l) <------------- --------------> favors neither, =
0
Compare the two tables above (one at time t= 0 and the other at equlibrium). Notice:
Summary: G determines if a reaction goes spontaneously in any given direction. If ΔG < 0, the reaction goes from reactants to products - to a state when products have a lower energy than reactants - like a ball rolling down a hill. Many factors contribute to ΔG, including ΔGconc , ΔGostab and ΔH. These are all energy terms and hence they will favor product formation if they are < 0. The other term which affects ΔG is ΔS. Entropy favors a product if ΔS >0. ΔS is not an energy term, but notice in the above equation that the term containing the contribution from entropy is -TΔS , where T is the temperature. This term is < 0, and favors product, if ΔS is positive (>0).
WCB Quiz: ΔG, ΔGostab, and ΔGconc
WCB Quiz: ΔG, ΔGostab, and ΔGconc - Answers
Speed of Reactions
We've learned a lot about chemical reactions, including:
One thing that we haven't studied is the speed (not extent) of a reaction. They are two very different concepts. Consider for example the simple reaction of octane with oxgyen.
This reaction is clearly exothermic (ΔH < 0) and proceeds with an increase in disorder (ΔS>0). Therefore, it is very favored in the forward direction. But you all know from experience that if you pour gasoline on to a table in the presence of air, nothing seems to happen. How can this be if the reaction is so favorable that it is essentially irreversible? A look at the diagram below shows how we can rationalize this behavior. If you think about it , the first thing that must happen in the reaction above is that some bonds in the products must be broken. This is clearly an endothermic process. Energy (through collisions) must be put into the reactants to do this. The molecules then go to a higher energy state. Eventually a few molecule then start forming stable bonds found in the product and in doing so, they release a lots of energy, in the form of heat. This released heat increases the temperature of the container, causing the molecules to have increased kinetic energy, increasing the number of collisions between reactant molecules which cause a cascade of bond breaking and making, resulting in a huge release of energy. This is why a spark is needed to "get the reaction going", even though it is greatly favored.
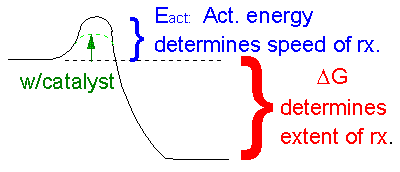
ANIMATION: ACTIVATION ENERGY AND A BALL ON A HILL