MOLECULAR MECHANICS AND DYNAMICS

04/13/16

A.  Introduction to Molecular Mechanics and Molecular Dynamics

Modeling modeling and computational chemistry are important parts of modern biochemistry.  Modeling is important to display in a meaningful and instructive fashion the large amounts of data produced when x-ray crystallography and NMR are used to determine the structure of large biological molecules and complexes.   Remember, however, that primary x-ray crystal data (in the form of electron density maps)  are just that, and the data must be interpreted like any other type of data.  Structures need to refined and energy minimized to produce more realistic structures (without van der Waals overlap or missing atoms, for example).  In addition, atoms within any molecule are not static, but move as bonds vibrate, angles bend, etc.  This implies that large biomolecules could adopt many possible conformations of different energies.  For proteins, some of these conformations might center around a average conformations situated at a local or global energy minimum separated from each other by activation energy barriers. 

In contrast to small molecules whose structure can be minimized using ab initio or semi-empirical quantum mechanics (using programs such as Spartan), large molecular structures (like DNA, RNA, proteins and their complexes) must be minimized using molecular mechanics, based on Newton's laws.  Atoms are treated as masses, and bonds as springs with appropriate force constants.  A force field, containing all the relevant parameters for given atom (for example sp3, sp2, sp2 aromatic, and sp C) and bond types is used to solve energy equations which sum all energies over all atoms and bonds in the molecule.  These energies include interactions among bonded atoms (stretching, bending, torsion, wagging) and those among nonbonded atoms (electrostatic and van der Waals).   For minimizations calculations, the positions of the atoms within a molecule must be systematically or randomly moved and the energy recalculated with the goal of finding a lower energy and hence more stable molecule.  Minimization calculations can not probe all conformational space and can not easily move a structure from a local minimum to a global minimum if two are separated by a large energy barrier.  Energy minimizations are usually done in the absence of solvent.  A common force fields used for macromolecules is CHARMM, AMBER, and GROMOS.  Parameters for specific atom type in a given bond include atomic mass, van der Waals radius, partial charge for atoms (from quantum mechanics) and bond length (from electron diffraction data), angles, and force constants for bonds (modeled as springs, obtained from IR).  These parameters are derived from experiments and theoretical (usually quantum mechanical) calculations on small organic molecules.  A potential energy equation comprised of terms from bond stretching, angle bending, and torsion angle changes (bonded interactions) as well as electrostatic and van der Waals interactions (nonbonded) is then solved (described below).

The goal of molecular dynamics is to simulate the actual changes in a molecule as a function of time after an energy input (heat application at a higher temperature) is added to a molecule at equilibrium.  To make the simulation realistic, the structure is placed in a "bath" of thousands of water molecules.  As is described below, if the energies of atoms in a large molecule are known, the forces acting on those atoms can be deduced.  From Newton's Second Law (F=ma), the velocity or change of position of an atom in the structure with time can be determined.  If the dynamic simulation can be run for a long enough period of time, alternate conformations (perhaps those centered around a global minimum as well as those nearby in energy space - a local minimum) may be sampled.  By determining what fraction of the simulated conformations resemble the two alternative conformations, the ΔG for the interconversion of the two states can be calculated.  As you can imagine, these calculations require large amounts of computer time.  They give very important information, however, since protein conformational changes are often, if not always associated with binding of a biological molecule to a binding partner.  In silico experiments offer important clues and support to results obtained using other methods of study.   

B.  Energy (E), Force (F) and Motion

To make the energy equations for the individual components more understandable, it is useful to consider the relationship between force and energy.  You have studied two general force equations in general chemistry and introductory physics.  One is Coulomb’s Law, which describes the electrostatic force of attraction, FC, between two charges, q1 and q2, separated by a distance r.

The other is Hooke’s Law, which describes the restorative force on a mass connected to a spring on stretching or compression of the spring.

where x is the displacement of the spring from an equilibrium (at rest) position. 

Our first interest is to understand how these equations might lead us to equations which describe the potential energy of a two charge system or of a compressed or stretched spring.  We can best understand this by studying the simple example of a ball placed at various locations on a hill.  If placed on a flat surface at the top and bottom of the hill, there is no net force on the ball (Fnet = 0), so it will not move.  If placed at various locations on the downslope, it will experience a net downward force, shown in a qualitative fashion in the figure below. 

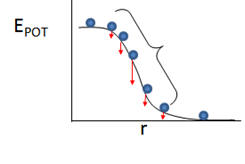
Astute observers will note that the magnitude of the force vector is proportional to the slope.  From this simplistic approach we come to the following equation relating F to E:

The minus sign is required since the force is downward but the energy increases upward.

This simplified approach can be extended into three dimensions, to give the following equation where F is the negative gradient of the potential energy:

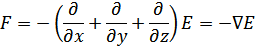
Applying the 1D equation to Hooke’s Law gives

This gives a parabolic graph of E vs displacement.

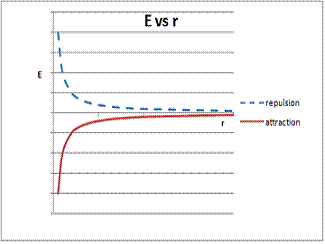
The same approach can be applied to Coulombs Law.  Notice that the result equation for E results in increasingly negative values as r get smaller only when q1 and q2 have opposite charges. 

A graph of E vs r for both attractive and repulsive interactions is shown below. 

A 3D energy landscape for the folding of a complicated protein molecule is shown below:

 EMBO reports 6, 1, 46–51 (2005) doi:10.1038/sj.embor.7400317. Published online: 17 December 2004
http://www.nature.com/embor/journal/v6/n1/fig_tab/7400317_f5.html

In this example, N is the native state at the global energy minimum, U is an unfolded state of a protein, and I is an intermediate state (a local energy minimum).  The black line represents a mechanically-induced unfolding pathway while the red is the trajectory for the folding pathway.  Both have a common intermediate.  Now lets consider molecular mechanics and dynamics in more detail.

The following review is based on an NIH Guide to Molecular Modeling, which was removed from the web, to the best of my knowledge,  in 1996.  I've recreated many of the graphs using Excel.

Molecular mechanics uses Newtonian mechanics to calculate energies of atoms in large molecules like proteins.  It assumes that nuclei and electrons are one particle with radii and calculated charged.  Bonds are treated as springs connecting atoms.  Energies are calculated classically (not with quantum mechanics).  Parameters, many based on QM calculations on small molecules, are assigned to all bonds, angles, dihedrals, etc.  Interactions are bonded (local) and nonbonded.

Bonded interactions involved atoms connected by one bond (bond stretch), two bonds (angle bending) and 3 bonds (dihedral angle change).

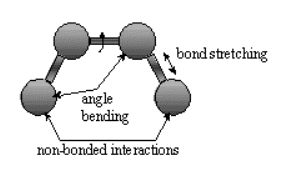
Non-bonded atoms (greater than two bonds apart) interact through van der Waals attraction, steric repulsion and electrostatic attraction/repulsion.

All energy terms from these interactions are summed to give the energy of a given conformation.  The energy should be considered relative to those of other conformations. Here is the basic energy equation for all of these energy terms:

Energy (E) = E _Stretch + E_Bending  + E_Torsion  +  E _{Non-bonded Interactions}

The "force field" consist of the energy equations and the parameters for each of the energy terms.  There are many different commercially available force fields.

D.  Bonded Interaction Energy

The mathematical form of the energy terms varies from force-field to force-field. The more common forms will be described.

Stretching Energy: E_stretch = Σ_bondsk_b (r - r_o)²

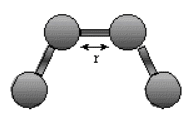
The stretching energy equation is based on Hook's law. The kb parameter defines the stiffness of the bond spring.  R₀ is the equilibrium distance between the two atoms.   It should make sense that deviations from the equilibrium length would be associated with higher energy.  The E vs r curves is hence a parabola:

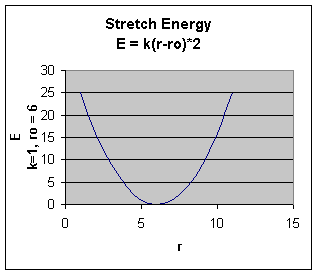
Obviously only small changes in r are allowed as to large an r value would lead to bond breaking.

Bending Energy: E_bending = Σ_angles k_Θ (Θ - Θ_o)²

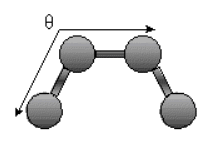The bending energy equation is also based on Hook's law. The kΘ parameter controls the stiffness of the angle spring, while the Θ₀  is the equilibrium angle. As above, the graph of E vs theta is expected to be a parabola.

. 

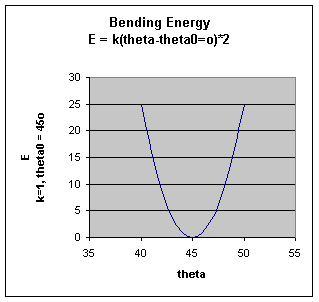
Torsion Energy E_torsion = Σ_torsions A [1 + cos ( ntau - phi) ] 

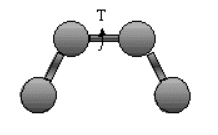
The torsion energy is modeled by a periodic function, much as you have seen with energy plots associated with Newman projections sighting down C-C bonds fro butane, for example. 

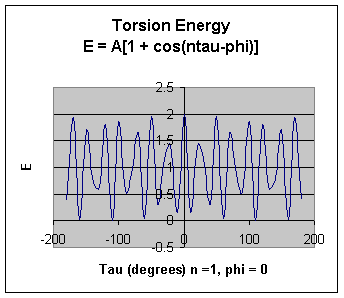
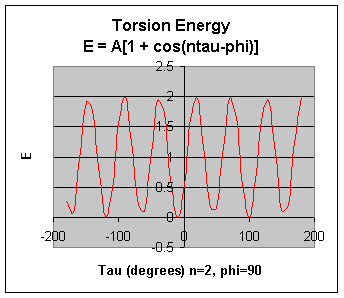
The parameters (determined for different 4 bonded atoms small molecules using curve fitting) for these are:

• amplitude A
• periodicity n (ethane, sighting along the C-C axis in a Newman projects displays a periodicity of 120 degrees)
• Phi:  shifts curve along rotation (tau) axis.  parameter controls its periodicity, and phi shifts the entire curve along the rotation angle axis (tau).

E.  Non-Bonded Interaction Energy

The non-bonded energy is calculated for all possible pairs of nonbonded atoms, i and j:

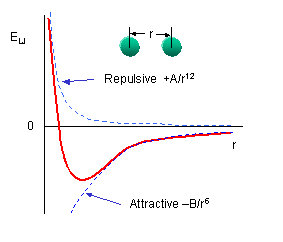
Enonbonding = Σi Σj [ -Bij/rij⁶ +A ij/rij¹² ] + Σi Σj (qi qj) / rij

The first term represents van der Waals interactions while the second terms represents Coloumbic electrostatic interactions.

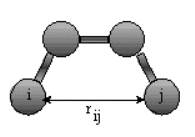
You should remember that van der Waals interactions are short range and occur among all atoms. The 6-12 energy equation based on the Lennard-Jones' potential, shows a negative (attractive) term proportional to -1/r⁶ and a repulsive term proportional to +1/r¹² :

I

The A and B parameters control the depth and position (interatomic distance) of the potential energy well for a given pair of non-bonded interacting atoms (e.g. C:C, O:C, etc.). In effect, A determined the degree of stickiness of the van der Waals attraction, and B determines the degree of hardness of the atoms (e.g. marshmallow-like, billiard ball-like, etc.).

The B parameter is related to the "stickiness" of the interactions and is related to the polarization of the atoms.  B can be obtained from atomic polarizability measurements, or it can be calculated quantum mechanically. The A parameter is empirically derived to fit nonbonded contacts between atoms in crystal structures. 

Lennard-Jones Interactive Applet

Couloumb's Law is used to calculate the electrostatic interactions based on appropriate dielectric constants (for buried or water accessible ion-ion pairs).

Enonbonding (electrostatic) =  Σi Σj (qi qj) / rij

A higher dielectric constant reflect more shielding by polar solvents of charge pairs. Partial charges on atoms are calculated using ab initio or semiempirical quantum mechanics.   (usually MOPAC or AMPAC).  The equation for the electrostatic potential is:

F.  Summary Interactions

Some programs assign charges using rules or templates, especially for macromolecules. In some force-fields, the torsional potential is calibrated to a particular charge calculation method (rarely made known to the user). Use of a different method can invalidated the force-field consistency.  Sometimes, an additional bonded interaction term, improper dihedrals, are added as illustrated below.  The potential for that is given by the following equation:

Eimproper = Σangles kω (ω - ωo)²

  All of the potential energy functions are illustrated in the graph below, where V is the potential energy.

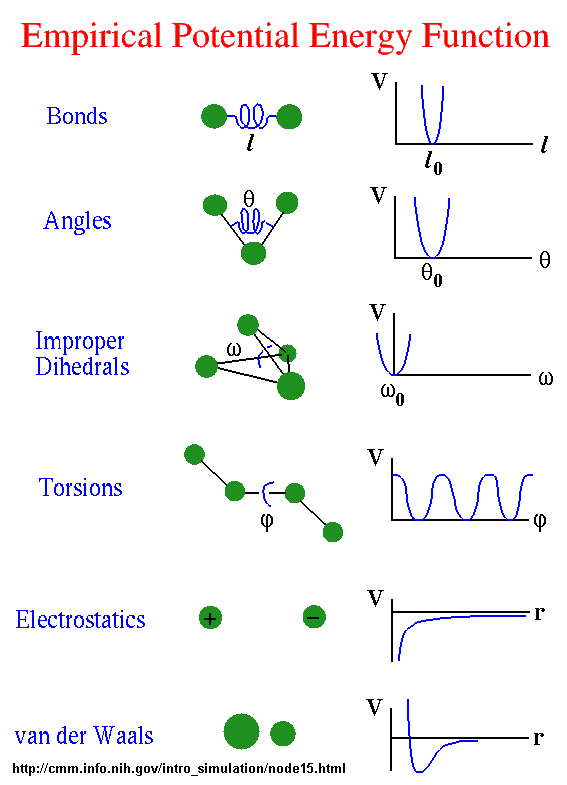
Go to this great web site by Sharon Hammes-Schiffer, Shaffer Associate Professor of Chemistry Theoretical and Computational Chemistry at Penn State to see interactive graphs for these potential functions.

G.  Molecular Dynamics

This section comes directly from the NIH tutorial:

"In the broadest sense, MD is concerned with molecular motion . Motion is inherent to all chemical processes. Simple vibrations, like bond stretching, and angle bending, give rise to IR spectra. Chemical reactions, hormone-receptor binding, and other complex processes are associated with many kinds of intra- and intermolecular motions.

The driving force for chemical processes is described by thermodynamics. The mechanism by which chemical processes occurs is described by kinetics. Thermodynamics dictates the energetic relationships between different chemical states, whereas the sequence or rate of events that occur as molecules transform between their various possible states is described by kinetics.

Conformational transitions and local vibrations are the usual subjects of molecular dynamics studies. MD alters the intermolecular degrees of freedom in a step-wise fashion, analogous to energy minimization. The individual steps in energy minimization are merely directed at establishing a down-hill direction to a minimum. The steps in MD, on the other hand, meaningfully represent the changes in atomic position, ri, over time (i.e. velocity).

Newton's equation (Fi = mi ai) is used in the MD formalism to simulate atomic motion. The rate and direction of motion (velocity) are governed by the forces that the atoms of the system exert on each other as described by Newton's equation. In practice, the atoms are assigned initial velocities that conform to the total kinetic energy of the system, which in turn, is dictated by the desired simulation temperature. This is carried out by slowly heating the system (initially at absolute zero) and then allowing the energy to equilibrate among the constituent atoms. The basic ingredients of MD are the calculation of the force on each atom, and form that information, the position of each atom through a s specified period of time (typically on the order of picoseconds = 10-12 seconds).

The force on an atom can be calculated from the change in energy between its current position and its position a small distance away. This can be recognized as the derivative of the energy with respect to the change in the atom's position: -dE/dri = Fi

Energies can be calculated using either MM or quantum mechanics methods. MM energies are limited to applications that do not involve drastic changes in electronic structure such as bond making/breaking. Quantum mechanical energies can be used to study dynamic processes involving chemical changes. The latter technique is extremely novel and of limited availability.

Knowledge of the atomic forces and masses can then be used to solve for the positions of each atom along a series of extremely small time steps (on the order of femtoseconds). The resulting series of snapshots of structural changes over time is called a trajectory. The use of this method to compute trajectories can be more easily seen when Newton's equation is expressed in the following form

-dE/dr_i = m_ia= md²r_i/dt²

In practice, trajectories are not directly obtained from Newton's equation due to lack of an analytical solution. First the atomic accelerations are computed from the forces and masses. The velocities are next calculated from the accelerations based on the following relationship:
ai = dvi/dt. Lastly, the positions are calculated from the velocities: vi = dr_i/dt. A trajectory between two states can be subdivided into a series of sub-states separated by a small time step, delta t (e.g. 1 fs).

The initial atomic positions at time t are used to predict the atomic positions at time t = delta t. The positions at t = delta t are used to predict the positions at t = 2delta t, and so on.

The leapfrog method is a common numerical approach to calculating trajectories based on Newton's equation. The method derives its name from the fact that the velocity and position information successively alternate at ½ time step intervals.

MD has no defined point of termination other than the amount of time that can be practically covered. Unfortunately, the current ps order of magnitude limit is often not long enough to follow many kinds of state to state transformations, such as large conformational transitions in proteins."

A quick-time movie of a molecular dynamics simulations of 86 water molecules, run for 1.6 ps, created using Quanta/Charmm!

QuickTime:  PhiPsi movement

MD simlulations can be used to obtained theoretical values for ΔG and Keq values for conformational changes, binding of small  ligands and changes in protonation states for side chains.   This process is based on the idea that the conformations sampled in in silico MD simulations reflect those found in vitro (i.e. they are part of the thermodynamically expected and available conformations available to the molecules during its normal conformational shifts).  This is called the Ergodic Hypothesis.  Given the short time spans for MD simulations (limited by computer power) this hypothesis can't apply to the dynamic results unless the sample conformations are close in energy without a large activation energy barrier between them.     If it is then the following equation could apply:

ΔG0 = -RTlnK_eq

ΔG0 = -RTlnP₂/P₁ = -RTlnf₂/f₁ where

Pn is the probability  of being in a given state and fn is the fraction in a given state.

You will note that none of the potential energy function use quantum mechanical parameters.  This is due, in part, to the complexity of the systems studied.   This is beginning to change as more effort is devoted to understanding quantum mechanical aspects of complex bonded systems.  New advances in even simple systems can illustrate this point.  Take for example ethane.  The conformational analysis of this simple molecule is discussed in all organic chemistry books.  Plots of energy vs dihedral angle (viewing the molecule down the C-C bond and measuring the angle between C-H bonds on adjacent C atoms) oscillates every 120^o.  The E is at a maximum when the dihedral angle is 0, 120, 240 and 360^o, each representing the eclipsed conformation.  It reaches minimums at the staggered (gauche) conformations at 60, 180, and 270^o.  Why is the eclipsed form higher in energy than the staggered form.  All organic books would state that there is greater steric repulsion (of the electron clouds) in the eclipsed forms, which raises their energy compared to the staggered forms?  However,  Pophristic shows that to be incorrect.  For the correct answer, you must turn to quantum mechanics and the phenomena of hyperconjugation.  The staggered conformation is energetically favored not since it is less sterically restricted, but since its is a lower energy form due to resonance like stabilization of the σ CH molecular orbitals.  There is greater correct phase overlap of σ CH and s* CH molecular orbitals on the adjacent Cs when they are in the staggered conformation than in the eclipsed form.

H.  Links and Reference

1. Pophristic, V. & Goodman, L.  Hyperconjugation not steric repulsion leads to the staggered structure of ethane. Nature. pg  411, 565 - 568 (2001). Also Weinhold, F. Chemistry: A New Twist on Molecular Shape.  Nature. 411, 539 - 541 (2001);
2. Autumn et al. Adhesive Forces of a single gecko foot hair.  (VdW interactions).  Nature. 405, pg 681 (2000)