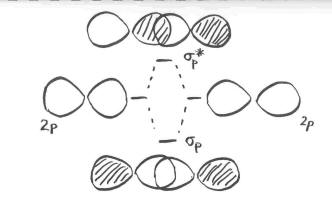
MO4. Sigma Bonding With p Orbitals
Other diatomic molecules in the upper right corner of the periodic table can be constructed in a similar way. Look at dinitrogen, N2.
We can think about how dinitrogen would form if two nitrogen atoms were placed close enough together to share electrons. Nitrogen has more electrons than hydrogen, so this interaction is more complicated.
In our qualitative examination of bonding in main group diatomics, we will take the approach used in Lewis structures and just look at the valence electrons. A quantitative molecular orbital calculation with a computer would not take this shortcut, but would include all of the electrons in the atoms that are bonding together.
Nitrogen has five valence electrons, and these electrons are found in the 2s and 2p levels. There are three possible atomic orbitals in the 2p level where some of these electrons could be found: px, py and pz. We need to look at the interaction between the s and px, py and pz orbitals on one nitrogen atom with the s and px, py and pz orbitals on the other nitrogen. That process could be extremely complicated, but:
- Orbital interactions are governed by symmetry.
Orbitals interact most easily with other orbitals that have the same element of symmetry. For now, we can simplify and say that orbitals on one atom only interact with the same type of orbitals on the other atom.
- s orbitals interact with s orbitals. We can already see how that will work out in dinitrogen, because that is what happened in dihydrogen.
- px orbitals interact with px orbitals.
- py orbitals interact with py orbitals.
- pz orbitals interact with pz orbitals.
Another complication here is that the s and p orbitals do not start out at the same energy level. When the orbitals mix, one combination goes up in energy and one goes down. Does the s antibonding combination go higher in energy than the combinations from p orbitals? Do the p bonding combinations go lower in energy than the combinations from s orbitals? We will simplify and assume that the s and p levels remain completely separate from each other. This is not always true, but the situation varies depending on what atoms we are dealing with.
- The combination of one s orbital with another is just like in hydrogen. Two old orbitals will combine and rearrange to produce two new orbitals.
- There is a bonding combination in which the orbitals are in phase. The new orbital produced has longer wavelength than the original orbital. It is lower in energy.
- There is an antibonding combination in which the orbitals are out of phase. The new orbital produced has shorter wavelength than the original orbital. It is higher in energy.
In considering the interaction of two p orbitals, we have to keep in mind that p orbitals are directional. A p orbital lies along a particular axis: x, y or z. The three p orbitals on nitrogen are all mutually perpendicular or orthogonal to each other. That situation is in contrast to s orbitals, which are spherical and thus look the same from any direction.

We first need to define one axis as lying along the N-N bond. It does not really matter which one. We arbitrarily say the N-N bond lies along the z axis. The pz orbitals have a different spatial relationship to each other compared to the py and px. The pz orbitals lie along the bond axis, whereas the py and px are orthogonal to it.

As the nitrogen atoms are brought together, one lobe on one pz orbital overlaps strongly with one lobe on the other pz orbital. The other lobes point away from each other and do not interact in any obvious way.
As with the s orbital, the pz orbitals can be in phase or out of phase. The in-phase combination results in constructive interference. (By "in-phase" here we mean the lobes that overlap are in-phase; for that to happen the two p orbitals are actually completely out of phase with each other mathematically, so that one orbital is the mirror image of the other.) This combination is at longer wavelength than the original orbital. It is a lower energy combination.

The out-of-phase combination (meaning in this case that the overlapping lobes are out of phase) results in destructive interference. This combination is at shorter wavelength than the original orbital. It is a higher energy combination.
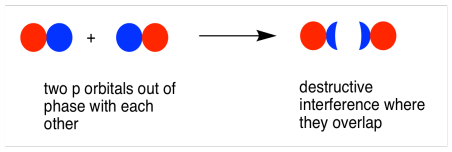
As a result, we have two different combinations stemming from two different p orbitals coming together in two different ways. We get a low-energy, in-phase, bonding combination and a high-energy, out-of-phase, antibonding combination.
What about those other p orbitals, the ones that do not lie along the bond axis? We'll take a look at that problem on the next page.
Problem MO4.1.
Draw an MO cartoon of a sigma bonding orbital formed by the overlap of two p orbitals between two oxygen atoms. Label the positions of the oxygen nuclei with the symbol "O". Label the O-O bond axis.
Problem MO4.2.
Consider the following reaction.
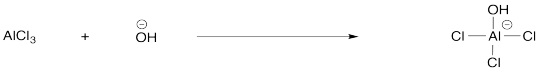
� Draw an MO mixing diagram for the reaction above:
o Draw the orbital
from the base that is likely to donate its electrons.
o Draw the
orbital from the acid that is likely to accept electrons.
o
Complete the MO mixing diagram of these two orbitals:
� Label the electron donating orbital
� Label the electron accepting
orbital
� Populate the MO mixing diagram with electrons
o
Draw a cartoon showing the mixing of these orbitals.
This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages. It is freely available for educational use.
 Structure & Reactivity in Organic, Biological and Inorganic Chemistry
by Chris Schaller is licensed under a
Creative Commons Attribution-NonCommercial 3.0 Unported License.
Structure & Reactivity in Organic, Biological and Inorganic Chemistry
by Chris Schaller is licensed under a
Creative Commons Attribution-NonCommercial 3.0 Unported License.
Send corrections to cschaller@csbsju.edu
Navigation: