SC10. Diastereomers and Physical Properties
- In a pair of diastereomers, some chiral centers are the same and some are opposite. The molecule is neither identical to nor the mirror image of its diastereomer.
Threitol is a metabolite closely related to carbohydrates. D-threitol is the enantiomer of L-threitol. The two are non-identical, but they are mirror images of each other. Both compounds can be crystallized, forming needle-like crystals. Both have melting points of 88-89oC. D-threose has an optical rotation [a]D= - 4.0 (c, 7 in H2O, but L-threose has an optical rotation [a]D= + 4.6 (c, 6 in H2O). You might notice that these two numbers are not exactly opposites, but if you have ever tried measuring an optical rotation yourself, you know that this is pretty good.
- Enantiomers have identical physical properties, except that the optical rotation is opposite.
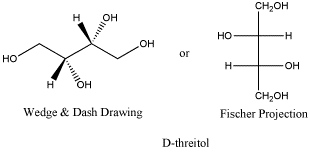
Figure SC10.1. D-threitol, a reduced form of threose.
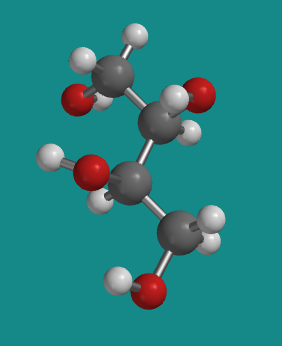
Figure SC10.2. A ball-and-stick model of D-threitol.
Go to Animation SC10.1. A three-dimensional model of D-threitol.
Here is the other anantiomer. Once again, the Fischer projection makes it really easy to see the difference, but navigating back and forth between Fischer and wedge-dash can be tricky. The ball-and-stick model is rotated a little compared to the model of D-threose; see if can confirm that this is really the enantiomer.

Figure SC10.3. L-threitol, the enantiomer of D-threitol.

Figure SC10.4. A ball-and-stick model of L-threitol.
Go to Animation SC10.2. A three-dimensional model of L-threitol.
Erythritol: a meso compound
Erythritol is a diastereomer to both L-threose and D-threose. It has one identical chiral center and one opposite one. Erythritol is a solid with a melting point of 121oC and no optical rotation. Erythritol has properties that are different from threitol.
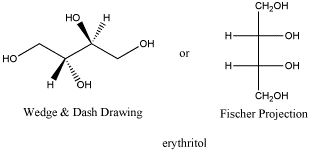
Figure SC10.5. Erythritol, the diastereomer of threitol.
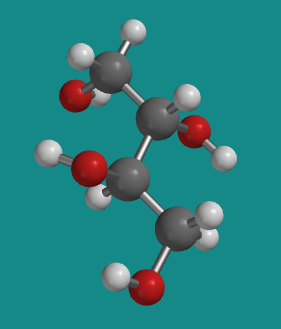
Figure SC10.6. A ball-and-stick model of D-threitol.
Go to Animation SC10.3. A three-dimensional model of erythritol.
- Diastereomers have different physical properties.
- They do not have the same overall shape.
- They fit together in different ways, and experience different intermolecular attractions.
The fact that erythritol contains chiral centers but has no optical rotation is unusual. Erythritol is chiral but not optically active. It is a special case called a meso compound.
- A meso compound contains two identical, opposite chiral centers.
- Rotation of plane-polarized light is canceled between these two centers, just like in a racemic mixture.
- Meso compounds are not optically active and do not have enantiomers, because the mirror image of a meso compound is itself.
It may be easier to see the mirror symmetry within erythritol if it is in a less-stable conformation. In the following model, the carbon backbone is held in a curled-up, eclipsed conformation rather than the usual zig-zag, staggered conformer. You might notice in the animation that this is really what we are looking at in a Fischer projection: the backbone is always curling away from us, with attached groups projecting towards us on either side. Here, the top half of the molecule is just a reflection of the bottom half.
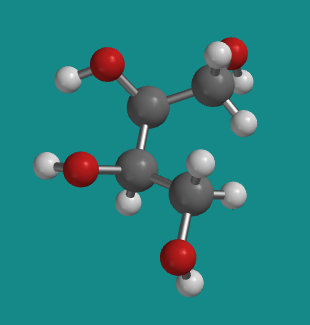
Figure SC10.7. A ball-and-stick model of erythritol in an eclipsed conformation.
Go to Animation SC10.4. Another three-dimensional model of erythritol.
Problem SC10.1.
What are the absolute configurations of each chiral carbon in:
a) D-threitol?
b) L-threitol?
c) erythritol?
Problem SC10.2.
In problem SC10.1., you should have numbered the carbons corresponding to each chiral center when you were denoting the absolute configuration. How did you know which end of the chain to start counting from?
Problem SC10.3.
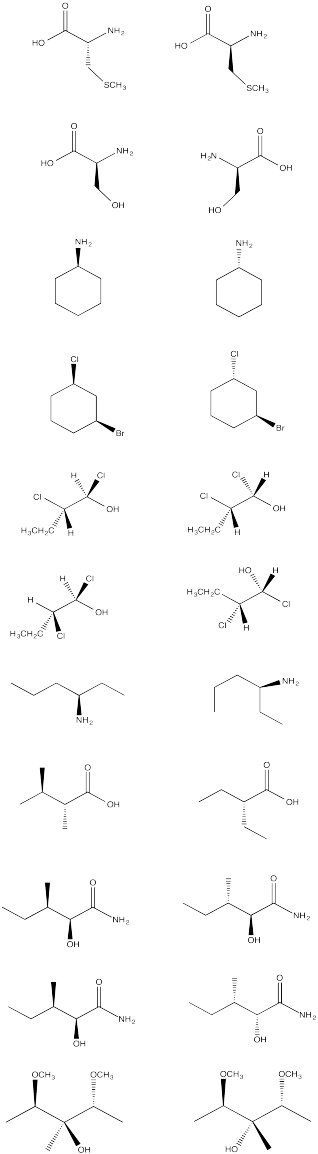
From the following group of molecules, select:
a) a pair that are the same compound.
b) a pair that would have the same physical properties but opposite optical activities.
c) a pair that have different physical properties.
d) a compound that contains chiral centers but has no optical activity.
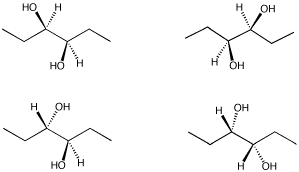
Problem SC10.4.
What is the isomeric relationship between the following pairs of molecules (diastereomers, enantiomers, constitutional isomers, identical)?