Biochemistry Online: An Approach Based on Chemical Logic

CHAPTER 1 - LIPID STRUCTURE
D: Lipids in Water - Thermodynamics
BIOCHEMISTRY - DR. JAKUBOWSKI
2/27/16
|
Learning Goals/Objectives for Chapter 1D: After class and this reading, students will be able to
|
Romanian
Translation √ by Alexander Ovsov
Ukranian Translation √ by Vlad Brown
Hindi Translation by Nathan Zed
Introduction to Chemical Potential
We have studied the intermolecular forces involved when single chain amphiphiles and double chain amphiphiles form micelles and bilayers, respectively. To gain a greater insight into the these processes, we need to understand the thermodynamics of micelle and bilayer formation. First we must understand the concept of chemical potential, which is related to the free energy of a reaction.
DG, the free energy chance for a reaction, determines the spontaneity and extent of a chemical or physical reaction. The free energy of system depends on 3 variables, T, P, and n, the number of moles of each substance. If the system is composed of two different parts, A and B, the system is at equilibrium (ΔG=0) if Ta = Tb, Pa = Pb, and dG/dn for A (μa) equals μb. μ is the chemical potential of a substance, where μa is given as μ=μo +RTln[A]. The chemical potential is really the free energy per mole.
Expressed in more formal mathematical terrms, since the natural variables of G and μ are T, P, and n, we can write:
dG = (ƒG/ƒT)P,n + (ƒG/ƒP)T,n + (ƒG/ƒn)P,T
where (ƒG/ƒx)y,z is the derivative (partial) of G with respect to x at constant y and z. That is the total dG consist of contributions to the change of G from changes in T, P and n.
Since G and m are quite similar, the following series of analogous equations apply:
ΔG = ΔGo + RTln Qrx is analagous to Δμ = Δμo + RTlnQrx
where Qrx is the reaction quotient = [P][Q]/[A][B] for the reaction A+B<==> P+Q
ΔG = ΔH - TΔS is analogous to Δμ =ΔH - TΔS
ΔGo = ΔHo - T ΔSo is analogous to Δμo = ΔHo - TΔSo
ΔGo = - RTlnKeq is analogous to Δμo = - RTln Keq
Thermodynamics of Micelle and Bilayer Formation
First, let's consider the thermodynamics of micelle formation, based on the equation below:
n SCA <==> 1 micelle
where SCA represents a single chain amphiphile. At first glance we might suspect that:
- ΔHo < 0 since the van der Waals interactions among the buried acyl chains in the micelle would be much more favorable than the water - acyl chain interactions for the monomeric amphiphile in solution. This notion is supported by our aphorism, "like dissolves like". Of course, we couldn't ignore polar interactions (H bonding for example) among the head groups and water, but we might expect these to be equally favorable in both the monomeric and micellular states.
- ΔSo < 0 since we are forming a state (a single micelle) with much less positional entropy from a state (single chains amphiphiles dispersed in solution) with much more positional entropy.
Hence it would appear that micelle formation is enthalpically favored but entropically disfavored. Lets examine this issue more closely. First we need to obtain a greater understanding of Δμo which should give us a clue as to where a SCA would "want" to be in this mixture. Remember, Δμo depends only on the relative stability of a molecule in a given environment and not its concentration.
Traube, in 1891, noticed that single chain amphiphiles tend to migrate to the surface of water and decrease its surface tension (ST.) He observed that the decrease in ST is directly proportional to the amount of amphiphile, added up until a certain point, at which added amphiphile has no additional effect. In other words, the response of ST saturates at some point.
We are more interested in what happens to amphiphiles in bulk water, not at the surface. As we mentioned earlier, monomeric single chain amphiphiles are in equilibrium with single chain amphiphiles in micelles. Assume you have a way to measure monomeric single chain amphiphile in solution. What happens to its concentration as you add more and more SCA to the mixture? Turns out you observe the same effect that Traube noted with changes in surface tension. This explanation goes like this: as more amphiphile is added, more goes into bulk solution as monomers. At some point, there are enough amphiphiles added to form micelles. After this point, added amphiphiles forms more micelles and no further increases in monomeric single chain amphiphile are noted. The concentration of amphiphile at which this occurs is the critical micelle concentration (CMC).
Figure: Graph showings distribution of single chain amphiphiles in bulk aqueous solution
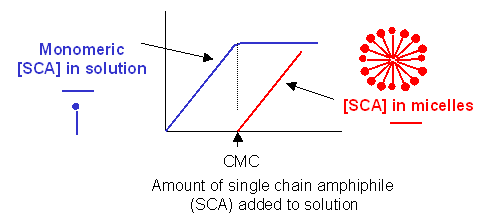
This saturation effect can be observed with other systems as well.
- measure the amount of NaCl(aq) in solution as more NaCl(s) is added to water. At some point, the water is saturated with dissolved NaCl, and no further increase in NaCl (aq) occurs.
- measure the amount of a sparing soluble hydrocarbon (HC) into water. After saturation, phase separation occurs.
Consider the example of adding a great excess of NaCl(s) to water. At the
very time the salt is added, the system is clearly not in equilibrium.
Therefore, Δμ<
0. Write the reaction as follows:
NaCl(s) ------------> NaCl (aq). Let x
stand for NaCl. Therefore,
Δμ = μ x(aq) - μ x(s) = μo x(aq) + RT ln x(aq) - (μo x(s) + RT ln x(s))
In this equation, all terms are constant except RT ln x(aq), since all the Δμ o values are constant, independent of concentration. Remember, RTln x(s) is constant since the concentration of a solid is constant. With time, Δμ becomes less negative, until the system reaches equilibrium, and Δμ = 0. The term RT ln x(aq) becomes more positive since the x(aq) is increasing. When μ x(aq) = μ x(s) , no further NaCl dissolves. Remember, a condition for equilibrium is μa = μb.
Now consider the addition of a drop of a slightly soluble hydrocarbon (HC) into water, as pictured in the diagram below. At t=0, the system is not at equilibrium and some of the HC will transfer from the pure liquid to water, so at time t=0, Δμ < 0.
Figure: Δμ for transfer of a sparingly soluble liquid solute into water
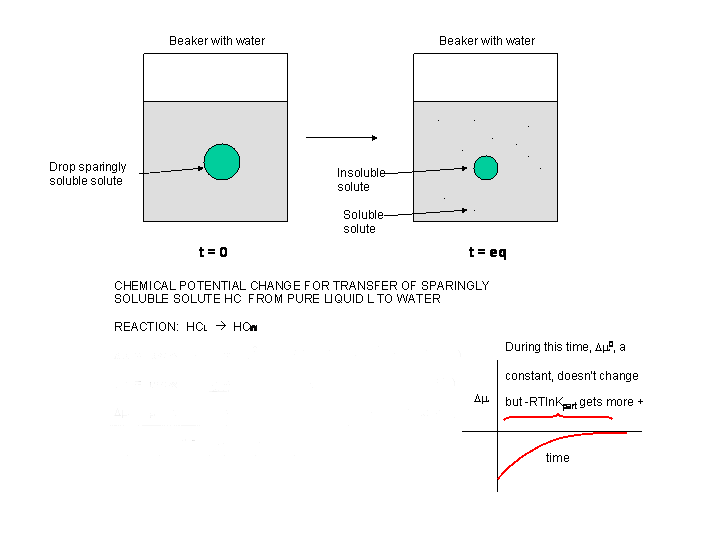
Δμ = μ HC-W - μ HC-L = μo HC-W + RT ln [HC-W] - (μo HC-L + RT ln [HC-L] =
Δμ = μ HC-W - μ HC-L = (μo HC-W - μo HC-L) + RT ln [HC-W - RT ln HC-L) =
Δμ= Δμo + RT ln (HC-W/HC-L)
Now add a bit more complexity to the last example. Add a hydrocarbon x, to a biphasic system of water and octanol. At t = 0, the system is not at equilibrium. A simple favorable reaction can be written for this system x aq -------> x oct. Clearly, Δμ < 0. Also, Δμo < 0, since this term is independent of concentration and depends only on the intrinsic stability of x in water in comparison to that of octanol. The following equation holds as well:
Δμ = μ x(oct) - μ x(aq) = μo x(oct) + RT ln x(oct) - (μo x(aq) + RT ln x(aq)) =
Δμ= (μo x(oct) - μo x(aq) ) + RT ln (x(oct)/x(aq)) =
Δμ = Δμo + RT ln (x(oct)/x(aq))
Most of the time, we will be interested in Δμo , which depends only on the relative stability, in this case, of x in octanol vs water. Clearly, in this case, Δμo < 0. At equilibrium Δμ = 0. By setting the last equation equal to 0, we can see that
Δμo = - RT ln (x(oct)/x(aq))
where the concentration are equilibrium concentrations. We can rewrite this equation as
Δμo = - RT ln Keq
where Keq is the equilibrium partition coefficient for X in octanol and water. This can readily be determined in the lab. Just shake a separatory flask with a biphasic system of octanol and water after injecting a bit of X. Then separate the layers and determine the concentration of x in each phase. Plug these numbers into the last equation. Remember, you should be able to predict the sign and relative magnitude of Δμo since it does not depend on concentration, but only on the intrinsic stability of the molecules in the different environments.
Introduction to the Hydrophobic Effect
Now we can apply our understanding of Δμo to the formation of
micelles and bilayers. Remember,
Δμo = ΔHo - T ΔSo..
The diagram below shows the standard free energies of transfer of a hydrocarbon X from aqueous solution to a pure liquid hydrocarbon (HC), x (aq) --------> x (HC).
Δμo = μo x(HC) - μo x(aq) , which should be less than 0. In each graph, Δμo is less than 0, and the value of Δμo decreases (gets more negative) in a linear fashion with increasing numbers of C in the alkyl chain. Notice the lines are unbelievably straight and parallel. Nature is speaking to us in these figures. By figuring out the surface area of the chains and the decrease in Δμo with each added CH2 (methylene group), one can calculate that the Δμo decreases by 25 cal/sq. angstrom of hydrocarbon chain added.
Figure: Standard free energy of transfer of HC from aqeuous solution to a pure liquid hydrocarbon.
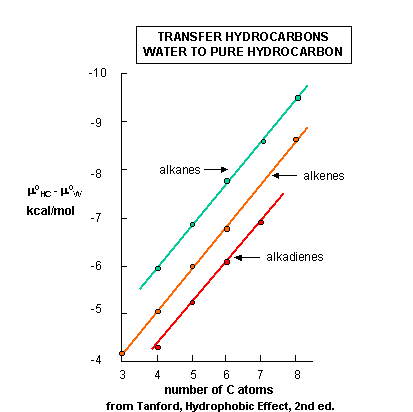
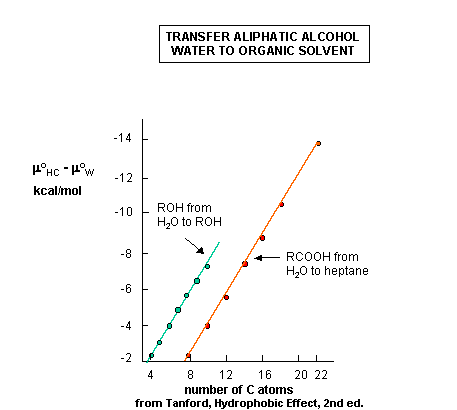
We expected that Δμo for the transfer of x to a pure liquid HC would be negative. The same is true for the transfer of aliphatic alcohols and fatty acids, both single chain amphiphiles, to organic solvents, as shown in the figure linked below. We could get more information if we would determine the entropic and enthalpic contributions. Such data is presented in the table below, which shows the transfer of single chain alcohols from the pure liquid to water (the opposite of the previous figures.) We expect the Δμo to be greater than 0 for these cases, since it should be disfavored. What is perplexing about this data is not that it is disfavored, but that the process is enthalpically favored . This seems to be counterintuitive since it goes against the adage that "like dissolves like" as was discussed earlier. From an enthalpic point of view, the amphiphiles prefer (albeit marginally) to be in water. What makes this reaction disfavored is entropy. The data shows that the aliphatic chains would prefer not to be in water because it is disfavored entropically. This seems to go against our notion from above that when single chain amphiphiles form micelles, it should be entropically disfavored. This chart shows us the if we were to take a single chain amphiphile from water into a micelle, (again the opposite of the direction used in this chart), that the entropy would be positive, and hence be favored!
Figure: Transfer of Aliphatic Alcohols and Fatty Acids from Water to Pure Liquid; Thermodynamic Parameters for Transfer of Aliphatic Alcohols From the Pure Liquid to Water.
The table below shows the thermodynamic parameters for transfer of HC from water into the interior of sodium dodecyl sulfate (SDS) micelles and from water to a pure HC liquid. Both of these processes are favored, since Δμ is less than 0. Notice once again what favors the process of a HC transferring from water into a micelle (which models at least part of micelle formation) is entropy not enthalpy. Enthalpy disfavors this process or, at minimum, is neutral.
How can we explain this counter-intuitive favorable entropic process. Again, at first glance it seems that entropy should disfavor micelle formation, since a single multimolecular aggregate of lower positional entropy (fewer possible microstates for amphiphile dispersal) is formed from many SCA. However, this is only part of the process. What we haven't considered is the entropy of water. To place a HC in water, a literal cavity in the water must be created that will accommodate the HC. Creation of this more ordered cavity must be entropically disfavored (again because the process proceeds to a state with fewer microstates and lower positional entropy) . Now transferring the HC from water to a micelle will dissipate the cavity, and lead to more available microstates for the released solvent, bulk water. It is this entropic contribution that favors micelle and hence bilayer formation. Image this scenario. When you place a HC group in water, water still wants to maintain its hydrogen bonding. Hence it is forced into a more ordered structure around the HC to maintain its H-bonding, characterized by fewer microstates. This effect, in which the spontaneous formation of micelles and bilayers is favored by the increase in entropy when water structured around the nonpolar part of the lipid is freed as the nonpolar part sequesters into the micelle and bilayer is driven by the Hydrophobic Effect.
Thermodynamic Parameters for Transfer of Aliphatic Alcohols from the Pure Liquid to Water at 25oC. (enthalpy determined by calorimeter)
| alcohol | μw0-μ ROH0 (cal/mol) | Hw0-H ROH0 (cal/mol) | Sw0-S ROH0 (cal/deg mol) | (Cp)w0-(Cp)ROH0(cal/degmol) |
| ethanol | 760 | -2430 | -10.7 | 39 |
| n-propanol | 1580 | -2420 | -13.4 | 56 |
| n-butanol | 2400 | -2250 | -15.6 | 72 |
| n-pentanol | 3222 | -1870 | -17.1 | 84 |
Thermodynamic Parameters for Transfer of Hydrocarbons from Water to Interior of Dodecyl Sulfate Micelles and from Water to Pure Liquid Hydrocarbon State
| Hydrocarbon |
Water --> Micelle Interior |
Water --> Pure Liquid Hydrocarbon |
||||
| ΔGo (kcal/mol) | ΔHo (kcal/mol) | ΔSo (cal/deg mol) | ΔGo (kcal/mol) | ΔHo (kcal/mol) | ΔSo (cal/deg mol) | |
| Ethane | -3.45 | +2.0 | +18.3 | -3.9 | +2.5 | +21 |
| Propane | -4.23 | +1.0 | +17.5 | -4.9 | +1.7 | +22 |
| Butane | -5.13 | 0 | +17.2 | -5.9 | +0.8 | +23 |
from Tanford, The Hydrophobic Effect (New York: Wiley, 1973)
How can we explain the favorable enthalpic contribution to place a nonpolar molecule into water? Again, this goes against our adage of "like dissolves like". The negative DH suggests interactions among all the participants are more favorable when the nonpolar group is in water. One source of such interactions could be the highly structured water in the "cage" that surrounds the nonpolar molecule. If it were more structured than bulk water, hence more "ice-like" in nature, then the formation of these extra H-bonds would contribute to the negative enthalpy change. When the nonpolar molecule is removed from the water, a process which proceeds with a positive ΔH, the cage of "ice-like" water would "melt", which, like the melting of ice, is not favored enthalpically. Heat energy must be supplied to break the H-bonds as ice changes state to liquid water. This molecular model to understand the thermodynamic data might yet be a simplistic model, but for time being, let's use it.
-
A Windows Media File (WMF) movie: Lipids and the Hydrophobic Effect

Biochemistry Online by Henry Jakubowski is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.