MB7. Solutions for Selected Problems

Problem MB1.1.

Problem MB1.2.

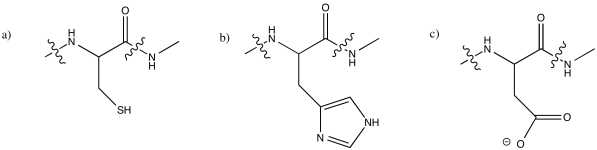
Problem MB1.3.

At neutral pH, lysine would normally be protonated.  It would noy have a lone pair on the nitrogen to coordinate a metal ion.

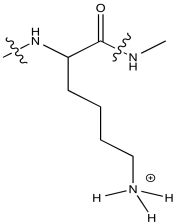
Problem MB4.6.

The pK_a of an α-position is typically about 20, although it can vary depending on what other groups are nearby. That is too high to build up a significant amount of the deprotonated species in water, which has a pK_a (in water) of 14.

Problem MB4.7.

a) The pK_a of the side chain of histidine is about 6.0; upon changing from pH 7 to pH 5, this group would become protonated and positively charged.  The positive charge would be more stabilising (or less destabilising) toward Fe²⁺ than Fe³⁺; the reduction potential would increase.

b) The pK_a of the side chain of histidine is about 3.7; upon changing from pH 4 to pH 3, this group would become protonated and positively charged.  The positive charge would be more stabilising (or less destabilising) toward Fe²⁺ than Fe³⁺; the reduction potential would increase.

c) The pK_a of the side chain of histidine is about 4.2; upon changing from pH 4 to pH 5, this group would become deprotonated and negatively charged.  The negative charge would be more stabilising (or less destabilising) toward Fe³⁺ than Fe²⁺; the reduction potential would decrease.

Problem MB5.1.

Ti⁴⁺ and Ca²⁺

Problem MB5.2.

F^- and HO^-

Problem MB5.3.

a)  Co²⁺ with  NO₂^-

b)  Mg²⁺ with CH₃CO₂^-

c)  Cu⁺ with RS^-

d)  Fe²⁺ with N₂

e)  Zn²⁺ with  imidazole

Problem MB5.4.

Choose the best match for the following metal ions.

a)  Fe³⁺ with asp

b)  Cu⁺ with met

c)  Zn²⁺ with his

d)  Cu²⁺ with his

e)  Co³⁺ with glu

Problem MB5.5.

Choose the amino acid residue that would have the effect on the metal ion as described, based on HSAB principles.

a) Increase the reduction potential of Cu²⁺: met.

b) Decrease the reduction potential of Fe³⁺: glu.

c) Make Cu⁺ easier to oxidise: his.

d)  Make Fe²⁺ easier to oxidise:  asp.

e)  Make Fe³⁺ easier to reduce:  cys.

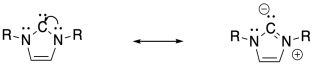
Problem MB6.1.

a)  The carbene is resonance-stabilized and aromatic.

b) PF₆ has a charge of 1-. The NHC ligand has no charge. The iron must be Fe(I).

c)  Isopropyl groups are larger than ethyl groups.  Steric croding probably forces the NHC ligands a little farther away from the iron with R = iPr compared to with R = Et.

d)  Because the NHC ligands do not donate as strongly with R = iPr compared to when R = Et, the Fe(II) state is relatively less stable with R = iPr, increasing the reduction potential (which becomes more positive / less negative).

e) 

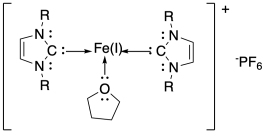
f)  The three-coordinate iron has fewer donors than the four-coordinate iron in the square planar complexes.  The lower electron density in the former case results in Fe(II) becoming relatively destabilized, leading to a more positive reduction potential.

g) Methyls groups are smaller than ethyl groups, so we expect less crowding from the NHC ligand with R = Me.  However, we often see bulky ligands adopt a tetrahedral geometry, because the 109 degree bond angle at the metal keeps the ligands further apart than the 90 degree bond angle in a square planar geometry.  In this case, the bulkier ligands adopt the square planar geometry, which should crowd the ligands more closely together.

h) Keeping all of these ligands in the square plane, but perpendiclar to the plane, allows them to stack, reducing steric crowding.

i)

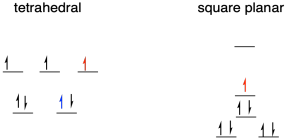
j) This time, it doesn't seem related to the metal-ligand bond lengths or the effective donation of electron density from the ligand to the metal, because then the trend in reduction potentials would be reversed.

If the Fe(II) tetrahedral species is low spin (possible because of the pi-accepting NHC ligand), then the electron donated upon reduction goes into the highest energy level, shown on red in the above picture.  In the square planar species, the electron is donated into a lower level, also shown in red.

If the Fe(II) tetrahedral species is high spin, however, then the electron is donated into the lower level.  If that's the case, it could be the pairing energy that makes this reduction slightly more difficult, as there is no corresponding price to pay in the square planar case.

Problem MB7.1.

a) 0 β            b) 1.73  β        c) 2.83  β        d) 3.87   β       e)  4.89  β       f)  5.92  β

Problem MB7.2.

a) approx. 4 β        b) approx. 4 β         c) approx. 2 β        d) approx. 3 β       

e) approx. 5 β        f)  approx. 0 β     g) approx. 6 β

This site is written and maintained by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with contributions from other authors as noted.  It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. 

This material is based upon work supported by the National Science Foundation under Grant No. 1043566.

Navigation:

Back to Redox Metals in Biology

Back to Reactivity Index

Back to Structure & Reactivity