RO7.  Batteries

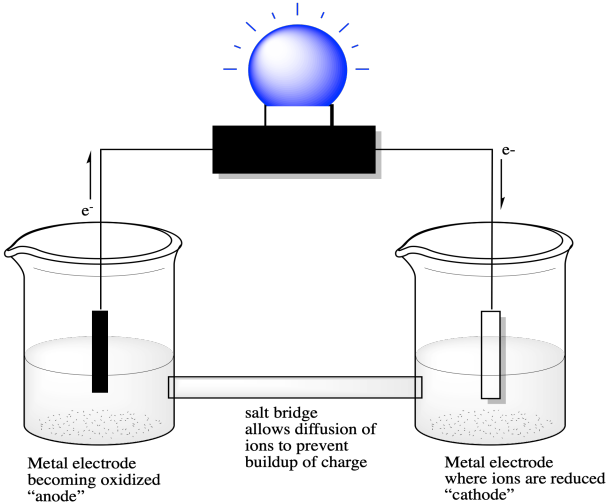
A measurement of a reduction potential involves connection of a circuit between two half-cells.  Electrons produced by an oxidation reaction in one half-cell must flow to the other half-cell, where a reduction reaction takes place.  If that flow of electrons is used to do work, we are using a chemical reaction to produce and harness electricity.  We have a battery.

   We might start by taking a strip of zinc metal and placing it in a beaker that contains some aqueous zinc salts, such as zinc nitrate, Zn(NO₃)₂.  We could also take a strip of  silver metal and place it in a beaker containing silver salts, such as silver nitrate, AgNO₃.  If we connected a copper wire from the silver metal to the zinc metal, the tendency of one metal to donate its electrons to the salts of the other metal would result in electrons running through the copper wire.  We could use that flow of electrons to power a small electronic device, such as a light bulb.

Figure RO7.1. A voltaic cell harnessed to power a light bulb.

   In this case, the reduction potential of the silver ion is more positive than the reduction potential of the zinc ion. 

Zn²⁺   +   2e^-    →    Zn_(s)            E^o = -0.762 V

Ag⁺   +   e^-     →      Ag_(s)            E^o = +0.796 V

   Electrons flow from the zinc metal, through the copper wire, to the silver metal.  At the surface of the silver metal, they are delivered to the silver ions in solution, converting them to silver metal. Since the zinc is being converted to zinc ion, the reaction is the opposite of what we see when we look at the reduction potential.  The potential is the opposite as well.  The reaction involving the silver ion remains the same.

Zn_(s)   →     Zn²⁺   +   2e^-            E^o = +0.762 V

   The potential of this overall reaction, zinc metal gives electrons to silver ion to form zinc ion and silver metal, is just the sum of those two potentials.

Zn_(s)   →     Zn²⁺   +   2e^-            E^o = +0.762 V

Ag⁺   +   e^-     →      Ag_(s)            E^o = +0.796 V

Zn_(s)   + 2 Ag⁺  →     Zn²⁺   +   2 Ag_(s)          E^o = +1.558 V

     In this treatment, we are using Hess' Law to combine those two reactions involving only zinc or only silver (sometimes called half-reactions) in such a way as to arrive at the overall reaction.  Because each zinc atom is giving up two electrons, and each silver ion only needs one electron to become a silver atom, then each zinc atom actually converts two silver ions to silver atoms.  However, there is no need to adjust the potential to account for that fact.  The net potential of the reaction is just telling us about the energetic distance between the donor orbital on zinc and the acceptor orbital on silver; that energy difference does not change depending on the number of atoms involved.

    If we were concerned about how much energy is given off when the zinc reduces the silver ion, then of course we would need to adjust for the number of electrons transfered.  Each time an electron jumps down from the donor orbital on zinc to the acceptor orbital on silver, it gives up more energy.  We can take that into account using Faraday's equation,

ΔG = -nFE^o 

Here, the delta G refers to free energy, n is the number of electrons transfered, F is Faraday's constant (96,485 J/V), and E^o is the reduction potential for the reaction.

Problem RO7.1.

Alkaline batteries are so-called because of the presence of hydroxide ion in the electrolyte.  The following reactions are typically involved:

ZnO_(s) + H₂O_(l) + 2e^-   →  Zn_(s) + 2OH^-                        E^o = - 1.28 V

2 MnO_2(s) + H₂O_(l) + 2e^- → Mn₂O_3(s) + 2OH^-_(aq)    E^o = + 0.15 V

a)  What is the potential produced by this battery?

b)  How much energy is produced by this battery?

Problem RO7.2.

There is a popular grade-school demonstration called "the lemon battery".  A galvanized nail (coated in zinc) and a penny are inserted into a lemon.  Alligator clips are attached and wires coming from the alligator clips are fastened to the leads on an LED.  With a little luck, the LED starts to glow.  Although you can't see it, protons from the citric acid in the lemon are converted to hydrogen gas.

a)  What is the potential for this cell?

b)  What is the energy produced in this reaction?

   There is some jargon that is useful to know when we are talking about batteries.  The parts of the battery that connect to the circuit (the wires and the electrical device powered by the battery) are called the electrodes.  Electrons flow out of one of these electrodes and into the circuit.  That electrode is considered the negative electrode and it is called the anode.  Electrons flow back out of the circuit, after powering the device, and back into the battery through the other electrode.  That electrode is considered the positive electrode and it is called the cathode.

   Sometimes, we describe a battery using cell notation.  Cell notation is a shorthand way of summarizing the chemistry of a battery or other electrochemical cell.  For example:

Zn�|Zn²⁺, SO₄^2-||SO₄^2-, Cu²⁺|Cu�

  This notation describes a battery with a zinc anode and a copper cathode.  The anode is always written at the left end of the notation and the cathode at the right.  Electrons are sent into the circuit from the zinc anode as the zinc is oxidized to zinc ion.  At the cathode, electrons are sent back into the battery so that copper ion is reduced to copper metal.  The single vertical lines that separate items in the notation represent phase boundaries between the solid metal and the aqueous solutions where the salts are found.  The double vertical line represents the separation between these two aqueous solutions, preventing the battery from short-circuiting.  Often, this double line is also read as a salt bridge, which maintains charge balance as zinc ions are produced on one side and copper ions are consumed on the other.  Other wise, the buildup of negative charge on one side and positive charge on the other would quickly stop the battery from working.

Problem RO7.3.

Provide the two half reactions that would occur in each of the following batteries:

a)  A lead acid car battery, in which the lead cathode conducts electricity but is not part of the reduction reaction:

Pb_(s) | PbSO_{4(s )} | H₂SO_4(aq) || H₂SO_4(aq) | PbO_{2 (s)} | PbSO_{4(s )} | Pb _(s)

b)  A nickel-cadmium battery:

Cd_(s)|Cd(OH)_{2 (s)} | OH^-_(aq) || OH^-_(aq) | NiO(OH)_(s) | Ni_(s)

c)  An alkaline flashlight battery (similar but not identical to one described earlier), in which a carbon cathode conducts electricity but is not part of the reduction reaction:

Zn_(s) | Zn(OH)_{2 (s)} | NaOH_(aq) || NaOH _(aq) | MnO_{2 (s)} | MnO₂H _(s) | C _(s)

Note that in some real batteries, the electrolyte is present as a paste.  Rather than being physically separated from each other, the two half reactions are prevented from short-circuiting by the very slow diffusion in this phase.  Often, you will see cell notation in which the components of the paste are not shown separated by vertical lines as done here, because they are actually mixed together.

Problem RO7.4.

The small silver oxide batteries used in watches, calculators and other small electronic devices use a silver (I) oxide cathode and a zinc anode.  The batteries are alkaline, meaning their electrolyte contains NaOH or KOH. 

a)  Use the appropriate reduction potentials to calculate the potential of the cell.

b)  Provide cell notation to describe the cell.

Problem RO7.5.

Proton-coupled electron transfers are thought to be very common in biochemistry. Investigators at CalTech and Washington set out to investigate this phenomenon in an iron porphyrin complex (Miller, Gray & Mayer, J. Phys. Chem. Lett. 2013, 4, 519-523).

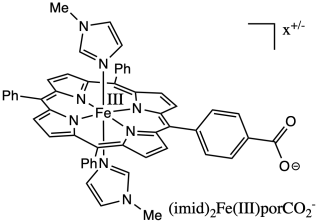
a)  Calculate the overall charge on the complex.

The pKa of (imid)2Fe(III)porCO2H was reported to be 20.2 at room temperature (300 K).

b)  If ΔΔG = -2.303 RT logK and pKa = -log Ka, calculate ΔG for deprotonation. Note that R = 8.314 J K^-1 mol^-1.

The reduction potential of (imid)₂Fe(III)porCO₂H was found to be -0.545 V; the reduction potential of (imid)₂Fe(III)porCO₂^- was -0.575 V.

c) Explain the difference in reduction potentials between the two species.

d)  If ΔG = -n F E^o, calculate ΔG for reduction to Fe(II), as in  (imid)₂Fe(II)porCO₂H. Note that F = 96,485 J V^-1 mol^-1.

e)  Calculate ΔG for reduction to Fe(II), as in  (imid)₂Fe(II)porCO₂^-.

f) The researchers couldn�t measure the pKa of the resulting Fe(II) species. Show how they used Hess� Law to calculate ΔG for deprotonation of (imid)₂Fe(II)porCO₂H.

g)  Explain the difference in deprotonation energies between the two species.

This site was written by Chris P. Schaller, Ph.D., College of Saint Benedict / Saint John's University (retired) with other authors as noted on individual pages.  It is freely available for educational use.

Structure & Reactivity in Organic, Biological and Inorganic Chemistry by Chris Schaller is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. 

Send corrections to cschaller@csbsju.edu

This material is based upon work supported by the National Science Foundation under Grant No. 1043566.

Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Navigation:

Back to Reduction and Oxidation

Back to Reactivity Index

Back to Structure & Reactivity