We have studied macromolecule structure. Now it is time to impart function to these molecules. It is simple to imagine that before these molecules can perform a function, they must interact with specific molecule(s) or ligand(s) in their environment. In fact, binding and subsequent release of a ligand might be the sole function of the macromolecule (example myoglobin binding oxygen).   Binding is the first step necessary for a biological response (with the exception of visual transduction in which photo-induced isomerization of rhodopsin initiates the response).  To understand binding, we must consider the equilbria involved, how binding is affected by ligand and macromolecule concentrations, and how to experimentally analyze and produce binding  curves.

A1.  Reversible Binding of a Ligand to a Macromolecule

These derivations can be made and interpreted using simple principles from General Chemistry, which you reviewed and strengthened in Analytical Chemistry, with some slight differences. Biochemists rarely talk about equilibrium or association constants, but rather their reciprocals - the dissociation constants, Kd.   For the reactions M + L ↔  ML, where M is free macromolecule, L is free ligand, and ML is macromolecule-ligand complex (which is held together by intermolecular forces, not covalent forces), the K_d is given by
[M]eq[L]eq/[ML]eq.

Figure: M is free macromolecule, L is free ligand, and ML is macromolecule-ligand complex

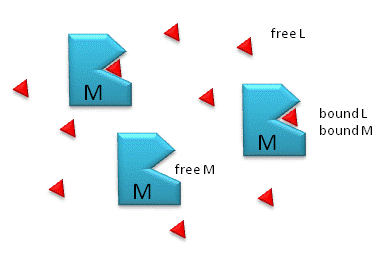
Notice the unit of Kd is molarity, M. The lower the Kd (i.e. the higher the [ML] at any given M and L), the tighter the binding. The higher the Kd, the looser the binding. Kd's for biological molecules are finely tuned to their environments. They vary from about 1 mM (weak interactions) for some enzyme-substrate complex, to pM - fM levels. Examples of very tight, non-covalent interactions include  the avidin (an egg protein)-biotin (a vitamin) and thrombin (enzyme initiating clotting)-hirudin (a leech salivary protein) complexes.

M = macromolecule; L = ligand

For a simple equilibrium M + L  <--> ML

where M = free macromolecule, L = free ligand, and ML = bound M and L (a complex)

3 equations can be written:

Equation 1 - Dissociation constant: K_d = ([M]eq[L]eq)/[ML]eq = ([M][L])/[ML] (units of molarity)

Equation 2 - Mass Balance of M: Mo = M + ML

Equation 3 - Mass Balance of L: Lo = L + ML

We would like to derive equations which give ML as a function of known or measurable values.  The Kd equations shows that ML depends on free M and free L.  From Equations 1-3, two different and equally valid equations can be derived for two different cases.  

• Case 1:  used either when you can readily measure free L or when experimental conditions are such the Lo >> Mo, which is often encountered.  Under these latter conditions, free L = Lo, which you know without measuring it, simply by knowing how much total ligand was added to the system.  
• Case 2 (more general):  used when you don't know free L or haven't measured it, and you just wish to calculate how much ML is present at equilibrium.  These conditions imply that  Lo is not >> Mo.  (If Lo >> Mo, we would know free L = Lo.) 

EXPERIMENTAL CASE 1: USE THIS FORM OF THE EQUATION WHEN L IS MEASURABLE OR WHEN Lo >> Mo (i.e. L= Lo)

Equation 4 - Substitute 2 into 1: K_d = ([M][L])/[ML] = [Mo-ML][L])/[ML]

(ML)Kd = (Mo)L - (ML)L

(ML)Kd + (ML)L = (Mo)L

(ML)(Kd+L) = (Mo)L

Equation 5: ML = MoL/(Kd + L)

This equation is ALWAYS TRUE for the chemical equation written above. L is the free ligand concentration at equilibrium.

Wolfram Mathematica CDF Player - Interactive Graph of ML vs L at different Mo and Kd values (free plugin required)

A downloadable version of the file for use with the free, standalone CDF player (no browser required)

Interactive SageMath Graph: ML vs L at different Mo and Kd values

If Lo >> Mo, then the equations simplifies to:

Equation 6: ML = MoLo/(Kd + L)..

Dividing Equation 5 by Mo gives the fractional saturation of the macromolecule M, where

Equation 7: Y = θ= [ML]/Mo = L/(Kd + L)

where Y can vary from 0 (when L = 0) to 1 (when L >> Kd)

Wolfram Mathematica CDF Player - Interactive Graph of Y vs L at different Kd values (free plugin required)

Graphs of ML vs L (equation 5) and ML vs Lo (equation 6), when Lo >> Mo, and Y vs L (equation 7) are all HYPERBOLAs
 

Equations 5.  ML = MoL/(Kd + L)   (and by analogy 6 and 7) can be understood best by examining three cases:

Case 1: L = 0, ML = 0

Case 2: L = Kd,  ML = MoL/(L + L)= MoL/2L = Mo/2

which indicates that M is half saturated. In fact the operational definition of Kd is the ligand concentration at which the M is half saturated.

Case 3: L >> Kd,  ML = Mo

EXPERIMENTAL CASE 2 (more general): USE THIS FORM OF THE EQUATION  WHEN FREE L IS NOT KNOWN (such as when Lo is not >> Mo) OR YOU WISH TO CALCULATE ML FROM JUST Lo, Mo AND KD

Equation 8 - Substitute 2 AND 3 into 1: K d = ([M][L])/[ML] = [Mo-ML][Lo-ML]/[ML]

(ML)Kd = (Mo - ML)(Lo - ML)

(ML)Kd = (Mo)(Lo) - (ML)(Lo) - (ML)(Mo) + (ML)2 or

Equation 9: (ML)2 - (Lo + Mo +Kd)(ML) + (Mo)(Lo) = 0, which is of the form

ax² + bx + c = 0, where

• a = 1

• b = - (Lo + Mo +Kd)

• c = (Mo)(Lo)

which are all constants, and

x = {-b +/- (b2 - 4ac)^1/2}/2a or

Equation 10: ML = {(Lo+Mo+Kd) - ((Lo+Mo+Kd)2 - 4MoLo)^1/2}/2

Wolfram Mathematica CDF Player - Interactive Graph of ML at various Lo, Mo, and Kd values (free plugin required)

A graph of ML calculated from this formula vs free L (or Lo if  Lo >> Mo) give a  A HYPERBOLA.

Play around with the sliders.  If you set Kd to a very low number and vary Mo, you will see a curve very much like a titration curve with a sharp rise and abrupt plateau that occurs when Mo is approximately equal to Lo. 

Interactive SageMath Graph: ML at various Lo, Mo and Kd values

In the derivations, we came up with two equations for ML:

• one (Equation 5) using mass conservation on M, which gave:    ML = MoL/[Kd +L]
• one (Equation 10) using mass conservation on M and L, which gave ML = quadratic equation as function of Mo, Lo, and Kd:  ML = {-(Lo+Mo+Kd) +/- ((Lo+Mo+Kd)2 - 4MoLo)1/2}/2

Both equations are valid. In the first you must known free L which is often Lo if Mo << Lo. In the second, you don't need to know free M or L at all.  At a given Lo, Mo, and Kd, you can calculate ML, which should be the same ML you get from the first equation if you know free L. 

Equations 5 and 10 are useful in several circumstances.  They can be used to

• calculate the concentration of ML if Kd, Mo, and L (for equation 5) or if Kd, Mo, and Lo (for equation 10) are known.  This is analogous to the use of the Henderson-Hasselbach equation to calculate the protonation state (HA) and hence charge state of an acid at various pH values.  In the former case we are measuring the concentration of bound ligand (ML) and in the later case, the concentration of bound protons (HA). 
• calculate Kd if ML, Mo, and L (for equation 5) or if ML, Mo, and Lo (for equation 10) are known.  Techniques to extract the Kd from binding data will be discussed in the next chapter section.

Navigation

Return to Chapter 5A:  Introduction to Reversible Binding Sections

Return to Biochemistry Online Table of Contents

 Archived version of full Chapter 5A:  Introduction to Reversible Binding