A2.  Interpretation of Binding Analyzes

It is important to get a mathematical understanding of the binding equations and graphs. It is equally important to get an intuitive understanding of their properties. Just as we used the +/- 2 rule in determining at a glance the charge state of an acid, you need to be able to determine the extent of binding (how much of M is bound with L) given their relative concentrations and the Kd. The usual situation is that [Mo] is << [Lo]. What happens to the binding curves for M + L <===> ML if the Kd gets progressively lower?  Intuitively, you should expect that binding will increase, especially as L gets greater. The curves below should help you develop the intuition you need with respect to binding equilibria.

Fig:  ML vs L at Varying Kd's

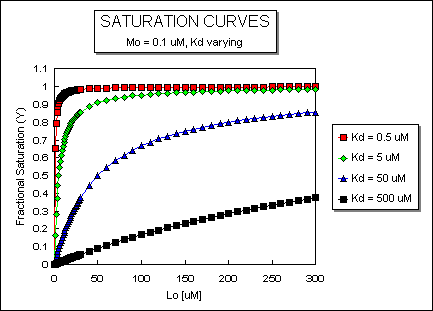
Fig:  ML vs L at Even Lower Kd's

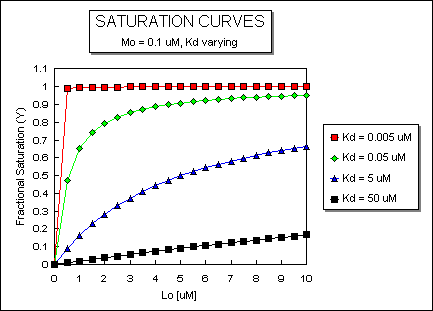
Fig:  ML vs L at a Very Low Kd!

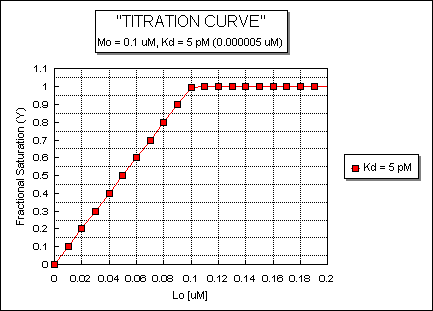
Note that in the last graph, given the same Mo and Lo concentrations, the "titration curves" for a binding equilibrium characterized by even tighter binding (for example, a Kd = 0.5 pM or 0.05 pM) would be indistinguishable from the graph when Kd = 5 pM.  It should be apparent that for all of these Kd values, all of the added ligand is bound until [Lo] > [Mo].  To differentiate these cases, much lower ligand concentrations would be required such that on addition of ligand, all is not bound.    Also note that this curve is NOT hyperbolic, which makes sense since the graph is of Y vs Lo, not Y vs L, and since Lo is not >> Mo.

Wolfram Mathematica CDF Player - Interactive Graph of Y vs L at two different Kd values (free plugin required)

Interactive SageMath Graph: Y vs L at 2 different Kd values

It is quite interesting to compare graphs of Y (fractional saturation) vs L (free) and Y vs Lo (total L) in the special case when Lo is not >> Mo.    Examples are shown below when Mo = 4 μM, Kd = 0.19 μM .  Under the ligand concentration used, it should be apparent the L can't be approximated by Lo.

Figure:   Y vs L and Y vs Lo when Lo is not >> Mo

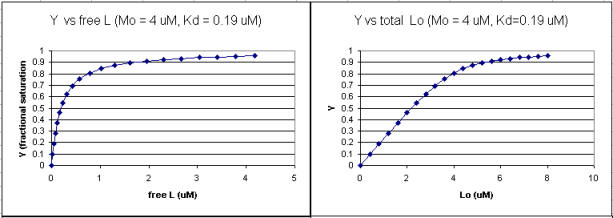
Two points should be evident from these graphs when  L is not approximated by Lo:

• a graph of Y vs Lo is not truly hyperbolic, but it does saturate

• a Kd value (ligand concentration at half-maximal binding) can not be estimated by inspection from the Y vs Lo, but it can be from the Y vs L graph.

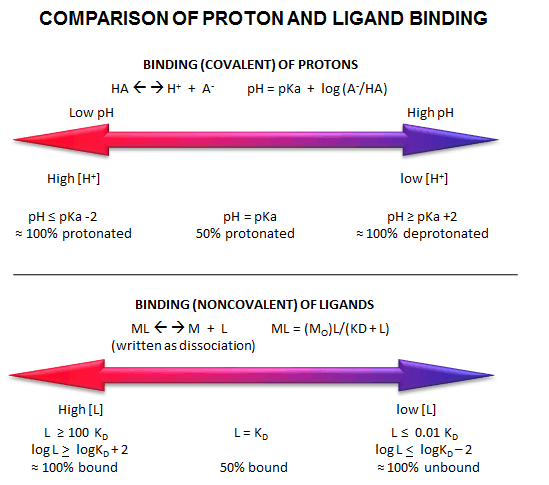
Fig:  Comparison of Covalent Binding of Protons vs Noncovalent Binding of Ligand

Navigation

Return to Chapter 5A:  Introduction to Reversible Binding Sections

Return to Biochemistry Online Table of Contents

 Archived version of full Chapter 5A:  Introduction to Reversible Binding