CHAPTER 5 - BINDING

A: INTRODUCTION TO REVERSIBLE BINDING

BIOCHEMISTRY - DR. JAKUBOWSKI

Last Update: 3/25/16

Learning Goals/Objectives for Chapter 5A: After class and this reading, students will be able to

write equations for the dissociation constant (KD), mass balance of total macromolecule (M0), total ligand (L0), and [ML] as a function of L or Lo ([ML] = [M0][L]/(KD+ [L]) (when Lo >> Mo or when free [L] is known) and Y = fractional saturation = Y = ([ML]/[M0] = [L]/(KD+ [L])
decide which of two given equations for [ML] should be used under conditions when the above conditions for L0 and L are given
based on the equation ([ML] = [M0][L]/(KD+ [L]) draw qualitative graphs for different given L0, L, and Kd values
determine fraction saturation given relatives values of Kd and L, assuming L0 >> M0
compare relative % bound for covalent binding of protons to an acid and noncovalent binding of a ligand to a macromolecule given pka/pH and Kd/L values
describe differences in binding curves for binding of a ligand to a macromolecule and the dimerization of a macromolecule
derive an equation which shows the relationships between the rate constant for binding (kon), dissociation (koff) and the thermodynamic dissociation (Kd) or equilibrium constant (Keq).
describe the structural and mathematic differences between specific and nonspecific binding
given a Kd, estimate t1/2 values for the lifetime of the ML complex.
describe techniques used to determine ML for given L or L0 values, including those that do and do not require separation of ML from M , so that Kd values for a M and L interaction can be determined
List advantages of isothermal titration calorimetry and surface plasmon resonance in determination of binding interaction parameters

A3. Dimerization and Multiple Binding Sites

In the previous examples, we considered the case of a macromolecule M binding a ligand L at a single site, as described in the equation below:

M + L <==> ML

where Kd = [M][L]/[ML]

We saw that the binding curves (ML vs L or Y vs L are hyperbolic, with a Kd = L at half maximal binding.

Dimerization

A special, yet common example of this equilibrium occurs when a macromolecule binds itself to form a dimer, as shown below:

M + M <==> M2 or D

where D is the dimer, and where

Equation 11: Kd = [M][M]/[D] = [M]2/[D]

At first glance you would expect a graph of [D] vs [M] to be hyperbolic, with the Kd again equaling the [M] at half-maximal dimer concentration. This turns out to be true, but a simple derivation is in order since in the previous derivation, it was assumed that Mo was fixed and Lo varied. In the case of dimer formation, Mo, which superficially represents both M and L in the earlier derived expression, are both changing.

One again a mass balance expression for Mo can be written:

Equation 12: [Mo] = [M] + 2[D]

where the coefficient 2 is necessary since their are 2 M in each dimer.

More generally, for the case of formation of trimers (Tri), tetramers (Tetra), and other oligomers,

Equation 13: [Mo] = [M] + 2[D] + 3[Tri] + 4[Tetra] + ....

Rearranging (12) and solving for M gives

Equation 14: [M] = [Mo] -2[D]

Substituting (14) into the Kd expression (1) gives

Kd = (Mo-2D)(Mo-2D)/D where can be rearranged into quadratic form:

Equation 15: 4D² - (4Mo+Kd)D + (Mo)² = 0

which is of the form y = ax2+bx+c. Solving the quadratic equation gives [D] at any given [Mo]. A value Y, similar to fractional saturation, can be calculated, where Y is the fraction of total possible D, which can vary from 0-1.

Equation 16: Y = 2[D]/[Mo].

A graph of Y vs Mo with a dimerization dissociation constant Kd = 25 uM, is shown below.

Figure: Saturation binding curve for dimerization of a macromolecule

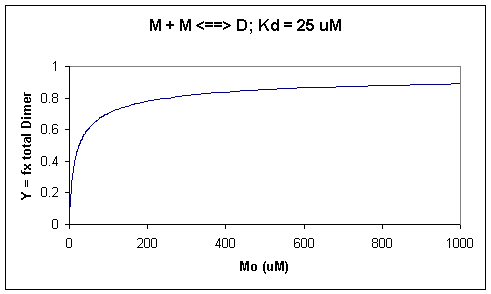
Note that the curve appears hyperbolic with half-maximal dimer formation occurring at a total M concentration Mo = Kd. Also note, however, that even at Mo = 1000 uM, which is 40x Kd, only 90% of the total possible D is formed (Y = 0.90). For the simple M + L <=> ML equilibrium, if Lo = 40x the Kd and Mo << Lo,

Y = L/(Kd+L) = L/[(L/40)+L] = 0.976

The aggregation state of a protein monomer is closely linked with its biological activity. For proteins that can form dimers, some are active in the monomeric state, while others are active as a dimer. High concentrations, such as found under conditions when protein are crystallized for x-ray structure analysis, can drive proteins into the dimeric state, which may lead to the false conclusion that the active protein is a dimer. Determination of the actual physiological concentration of [Mo] and Kd gives investigators knowledge of the Y value which can be correlated with biological activity. For example, interleukin 8, a chemokine which binds certain immune cells, exists as a dimer in x-ray and NMR structural determinations, but as a monomer at physiological concentrations. Hence the monomer, not the dimer, binds its receptors on immune cells. Viral proteases (herpes viral protease, HIV protease) are active in dimeric form, in which the active site is formed at the dimer interface.

Wolfram Mathematica CDF Player - Dimerization of Macromolecule (free plugin required)

SageMathLogo Interactive SageMath Graph: Dimerization of Macrmolecule

Binding of a ligand to two independent sites

Another Special Case: Binding of L to 2 sites with different Kds

Check out the interactive graph to see how the relative sizes of the Kds affect it.

Wolfram Mathematica CDF Player - Binding of L to 2 Sites (free plugin required)

SageMathLogo Interactive SageMath Graph: Fractional Saturation 2 Independent Sites

back Navigation

Return to Chapter 5A: Introduction to Reversible Binding Sections

Return to Biochemistry Online Table of Contents

Archived version of full Chapter 5A: Introduction to Reversible Binding