Biochemistry Online: An Approach Based on Chemical Logic
CHAPTER 5 - BINDING
C: MODEL BINDING SYSTEMS
BIOCHEMISTRY - DR. JAKUBOWSKI
3/29/16
|
Learning Goals/Objectives for Chapter 5C: After class and this reading, students will be able to
|
C10. Macromolecule Oligomer Formation and Symmetry
Many proteins are found in aggregated states and have quaternary structure. Hemoglobin consists of two alpha and two beta monomers (or protomers) which assemble to produce the biologically relevant heterotetrameric protein. As we discussed in Chapter 5A - Reversible Binding I, a given monomer can self aggregate to form homooligomers (dimers, trimers, tetramers, or Mn). The polymers display symmetry with respect to the geometric arrangement of the subunits. Symmetry, as we have just seen, is an important component of the MWC model. Most oligomeric proteins contain protomers that are symmetrically arranged. What mechanism determines whether a monomeric protein forms a homooligomer? Why do they stop at a certain n value? Can proteins be engineered to do so? If mutation can induce oligomer formation, then fewer mutations would be required to produce a symmetric oligomer from subunits since fewer mutations would be required as a single mutation in a single monomer would be represented n times in a single oligomer of n monomers. This fact probably underlies the reason that oligomers display exquisite symmetry. Hence a basic knowledge of symmetry of protein oligomers is necessary.
In the study of small molecules, chemists describe symmetry through the use of mathematical symmetry operations and elements, which find great use in analysis of structure and in molecular spectroscopy. These concepts are usually first encountered in physical and inorganic chemistry classes. A symmetry operation is a movement of an object like a molecule that leads to an identical, superimposable molecule.. Each operation has a symmetry element (point, line, or plane) about which the motion occurs. Some examples are shown below:
Table: Symmetry Elements and Operations
| Element (with Jmol link) | Operation |
| inversion center (i) | projection through center (point) of symmetry of point x,y,z to point -x,-y,-z |
| proper rotation axis (Cn) | rotation around a Cn axis by 360o/n where C denotes Cyclic |
| horizontal (σh) and vertical (σv) symmetry plane | reflection across a horizontal or vertical plane |
| improper rotation axis (Sn) | rotation around a Sn axis by 360o/n followed by reflection in plane perpendicular to the axis. |
Luckily for students trying to apply these rules to protein oligomers, biomolecules made up of chiral monomers (such as the L-amino acids of proteins) can not be converted to identical structures using inversion or reflection since the chirality of monomer would change - for proteins this would entail and L to D amino acid change. That excludes all but proper rotation axes (Cn) from the list above.
A point group is a collection of symmetry operations that define the symmetry about a point. The 4 types of symmetries around a point are those described above: rotational symmetry, inversion symmetry, mirror symmetry, and improper rotation. The types of point groups around a point include:
-
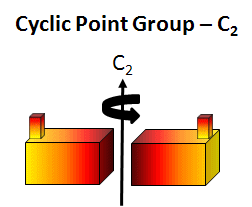
cyclic (Cn) - contain one single Cn rotation axis. A biological example is the tobacco mosaic virus double disk (34 monomers, C17). In this point group note that the n in Cn is equal to the number of monomers and the angle of rotation is 360o/n.
Figure: C2 Symmetry
-
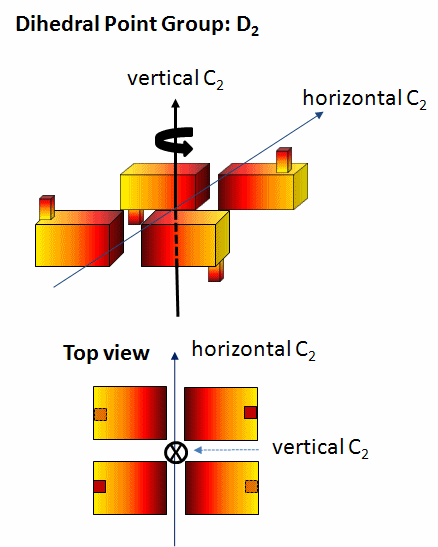
dihedral (Dn) - These have mutually perpendicular rotation axes. Specifically they contain at least 1 C2 axis perpendicular to a Cn axis (Canter and Schimmel. Biophysical Chemistry - Part 1). The minimal number of subunits is n. Most protein oligomers fall into this category. The packing (or asymmetric) unit does not have to be a single monomer but could be a heteodimer.
-
A D2 point group has 1 C2 axis and 2 perpendicular C2 axes, and 4 monomers (like Hb). These proteins can dissociate into two dimers (such as two α/β dimers for Hb). Note that a different arrangment of 4 monomers could produce a oligomer with C4 symmetry instead of D2.
-
A D4 point group has 1 C4 axis and 4 C2 axes, along with 2n=8 subunits. An example of a D4 point group is ribulose bisphosphate carboxylase/oxygenase (RuBisCO) which has 8 subunits (where a subunit, or more technically the assymetric subunit, is a dimer of a small and large molecular weight protein). This point group could arise from quaternary structure of two C4 tetramers or four C2 dimers.
-
Figure: D2 Symmetry
-
cubic - contain four C3 axes connecting opposite corners of a cube (so the lines are effectively diagonals) arranged as the four body diagonals (lines connecting opposite corners) of a cube. The tetrahedron (4 sides), cube (6), octahedron (8), and icosohedron (20), perfect Platonic solids (in which all faces, edges and angles are congruent) all have related 3 C3 axes (diagonals connecting opposite corners for cubes, diagonals from a vertex to the opposite face for tetrahedrons, line connecting two opposite faces for octahedron, etc ) so they all can be considered to be part of the cubic point group.
Cubes have a total of 13 symmetry axes comprising 3 types (three C4 axes passing through the centers of opposite faces, four C3 axes passing through opposite vertices, and six C2 axes passing through the the centers of opposite edges). On octahedron can be aligned with a cube and be shown to have the same symmetry axes.
-
Flash movie: Cube (red) and Octrahedron (blue) with 13 symmetry axes.
Tetrahedrons have a total of 7 symmetry axes comprising two types (four C3 axes of the cube and three C2 axes which are the same as the C4 axes of the cube. First note the relationship between a cube and an inscribed tetrahedron.
-
Flash movie: Tetrahedron with 7 symmetry axes.
A dodecahedron with 12 regular pentagon faces (green) and an icosohedron with 20 equilateral triangle sides (red) can be aligned with each other (as can cubes and octahedrons) and have 31 symmetry axes, as shown below. Note also the relations between a cube inside a dodecahedron and a octahedron inside of a dodecahedron that makes sharing of symmetry axes between these pairs more obvious.
-
Flash movie: dodecahedron and icosohedron with 31 symmetry axes.
vrml files for movies from http://www.georgehart.com/virtual-polyhedra/symmetry_axes.html
Examples of protein complexes with these point groups are:
-
aspartate-ß-decarboxylase, tetrahedral, 12 asymmetric units
-
dihydrolipoyl transsuccinylase, octahedral, 24 asymmetric subunits
-
many spherical viruses, icosahedral, 60 asymmetric units
![]() Jmol: Updated
Symmetry in Protein Oligomers (beta version with lots of work left to do)
Jmol14 (Java) |
JSMol (HTML5)
Jmol: Updated
Symmetry in Protein Oligomers (beta version with lots of work left to do)
Jmol14 (Java) |
JSMol (HTML5)
Proteins, especially those involved in cytoskeletal filaments, can form fibers which contain helical symmetry which differs from those described above since the monomers at the ends of helical fibers, although they have the same tertiary structures as those in the middle of the helical fibers, do not contact the same number of monomers as monomers internal in the oligomer and hence have different microenvironments.
A recent article by Grueninger et al. addresses the question of whether the process of oligomerization can be programmed into the genome. Can simple amino acid substitutions lead to oligomerization? Remember that oligomerization can be beneficial (formation of cytoskeleton filaments) or detrimental (formation of fibers in sickle cell anemia and mad cow disease). Oligomers with long half-lives (for example cytoskeletal filament such as actin and tubulin) and short half-lives (for example proteins causes transient activities are regulated by oligomer formation) are both necessary.
It has long been noted that if a protein chain forms oligomers, then a single amino acid change in the chain would be found n times in an oligomer of n chains. Mutations could either promote chain contact and oligomer formation or dissociation into monomeric or other asymmetric subunit composition if the mutation were in a region involved in subunit association (a contact region). Experimental work in this field of study is hampered by the fact that mutants made by site-specific mutagenesis to prefer the monomeric state often fail to fold (due to hydrophobic exposure and aggregation. Studies have shown that most contact areas between monomers or other asymmetric units are hydrophobic in nature and the contact regions must be complementary in shape. Obviously mutations that replace hydrophobic side chains involved in subunit contact with polar, polar charged, or bulkier hydrophobic side chains would inhibit oligomer formation.
Grueninger et al were able to successfully engineer dimer formation and oligomer formation as well. First consider the simplest case of a mutation in a monomer that can produce a dimer with C2 symmetry. This is illustrated below which also shows how a mutation that produces a weak interaction in a monomer could also produce a long helical aggregate (which can't be crystallized) without symmetry (as described above). A mutation at 2 could promote either oligomer helix formation or dimerization.
Figure: Mutations causing Dimer with C2 symmetry or Infinite Helix

(adapted from Grueninger et al. Science, 319, 206-209 (2008)
It should be noted that mutation could lead to dimer or oligomer formation by producing a more global conformational change in the monomer (not indicated in the example above) which leads to aggregate formation, as we have seen previously in the formation of dimers and aggregates of proteins associated with neurodegenerative diseases (like mad cow disease).
Grueninger produces mutants of two different proteins that showed dimer formation as analyzed by gel filtration chromatography (but did not crystallize so no 3D structures were determined). In addition the group modified urocanase, a C2 dimer, at 3 side chains to form a tetramer with D2 symmetry. Also, they modified L-rhamnulose-1-phosphae, a C4 tetramer, at a single position to form an octamer with D4 symmetry. The latter two were analyzed through x-ray crystallography. Their work suggests ways that complex symmetric protein structures arose in nature from simple mutation and evolutionary selection.
Navigation
Return to Chapter 5C: Model Binding Sections
Return to Biochemistry Online Table of Contents
Archived version of full Chapter 5C: Model Binding Systems

Biochemistry Online by Henry Jakubowski is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.