CHAPTER 5 - BINDING

C:  MODEL BINDING SYSTEMS

BIOCHEMISTRY - DR. JAKUBOWSKI

3/29/16

C4.  Mathematical Analysis of Cooperative Binding - MWC Symmetry Model

In the model MWC (Monod, Wyman, and Changeux) model, in the absence of ligand (oxygen), Hb exists in two distinct conformations, the T state (equivalent to the crystal structure of deoxyHb) and the R state (equivalent to the crystal structure of oxyHb without the oxygen). In the absence of dioxygen, the T state (T0) is greatly favored over the unliganded R state  (R0) at equilibrium. An equilibrium constant (more equivalent to a dissociation constant) can be defined as L = T0/ R0.  (Note:  L is not the ligand concentration.)  In addition, let us assume that Hb can not exist with some of the monomers in a tetramer in the T state while others in the same tetramer are in the R state. Hence this model is often called the symmetry model. Finally lets assume that each oxygen can bind to either the T or R state with the dissociation constants KT and KR respectively. These constants do not depend on the number of oxygens already bound to the tetramer. Hence KR = [R0][O2]/[R1] = [R1][O2]/[R2] = ... etc., where the subscript on R refers to the number of oxygens bound to that form of R.

Figure:   LINKED EQUIIBRIA IN THE MWC MODEL

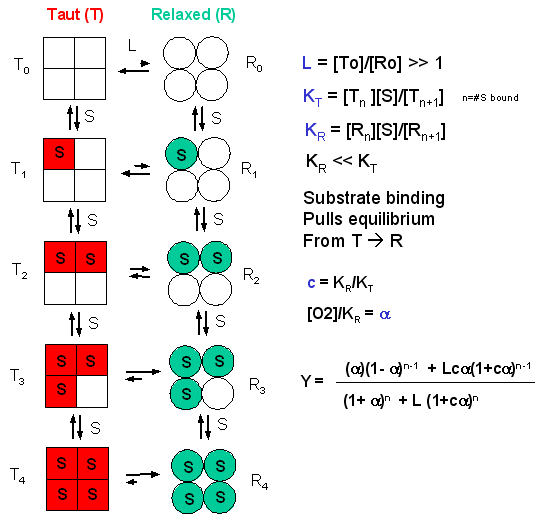
Now define two new parameters:
α = [pO2]/KR which is really a normalized ligand concentration describing how many times the KR the ligand concentration is.

c = KR/KT.

If oxygen binds preferentially to the R form of Hb, c would be a small fractional number. In the limiting case, when oxygen didn't bind to the T form, KT would be infinite, and c would equal 0.

Using these definitions and equations, the following equation showing Y, fractional saturation vs α can be derived, with n, the number of binding sites per molecule, = 4 for Hb.

Y = [α (1+α)n-1 + Lcα(1+cα)n-1]/[(1+α)n +L(1+cα)n]

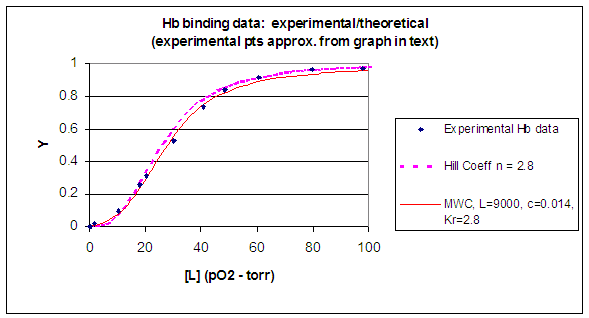
 Figure:  Y Vs alpha with varying L and c - MWC MODEL

When L is set at 9000 and c = 0.014, the Y vs α curve fits the experimental oxygen binding data well. The graph below shows the best experimental dioxygen binding data that I could find (obtained from a graph, not from a table), and the best fit Y vs L using a Hill coefficient of n=2.8 (fitting equation 3 above), and the best fit of Y vs L using the MWC model, with L=9000, c=0.014, and Kr = 2.8 torr. 

Figure:  Hb binding curves:  Experimental, vs Theoretical Hill and MWC Equations

Wolfram Mathematica CDF Player - MWC Model: download free CDF player and play this file.

Interactive SageMath Graph: MWC Model

• Interactive Hb:O2 Plots
• Interactive Mb, Hb plots

Another way to think about the MWC Model

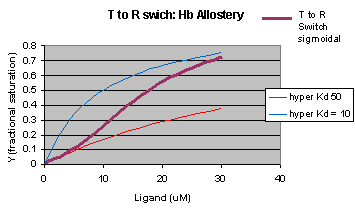
The MWC model assumes that oxygen binds to either the T or R form of Hb in a noncooperative fashion. That is KT and KR are constant, independent of the number of oxygens bound to that form.  If that is so, what is the basis of the cooperative oxygen binding curves?  The answer can be seen below.  The red curve might reflect the binding of a ligand to the T form of a macromolecule, with Kd = 50 uM, for example.  Notice that the binding curve is hyperbolic.  Likewise, the blue curve might reflect the binding of a ligand to the R form of the macromolecule with Kd = 10 uM.  If the T and R form are linked through the T <==> R equilibrium, this equilibrium will be shifted to the tighter binding R form with increasing ligand concentration, assuming that the ligand binds preferentially to the R form.  This shifts the actual binding curve from that resembling the T form at low ligand (red) to that of the R form as ligand increases (blue), imparting sigmoidal characteristics to the actual binding curve (purple).

Figure: Cooperativity as transition between two hyperbolic binding curves with different Kd's

Navigation

Return to Chapter 5C:  Model Binding Sections

Return to Biochemistry Online Table of Contents

 Archived version of full Chapter 5C:  Model Binding Systems