MOLECULAR MECHANICS AND DYNAMICS

04/13/16

B.  Energy (E), Force (F) and Motion

To make the energy equations for the individual components more understandable, it is useful to consider the relationship between force and energy.  You have studied two general force equations in general chemistry and introductory physics.  One is Coulomb’s Law, which describes the electrostatic force of attraction, FC, between two charges, q1 and q2, separated by a distance r.

The other is Hooke’s Law, which describes the restorative force on a mass connected to a spring on stretching or compression of the spring.

where x is the displacement of the spring from an equilibrium (at rest) position. 

Our first interest is to understand how these equations might lead us to equations which describe the potential energy of a two charge system or of a compressed or stretched spring.  We can best understand this by studying the simple example of a ball placed at various locations on a hill.  If placed on a flat surface at the top and bottom of the hill, there is no net force on the ball (Fnet = 0), so it will not move.  If placed at various locations on the downslope, it will experience a net downward force, shown in a qualitative fashion in the figure below. 

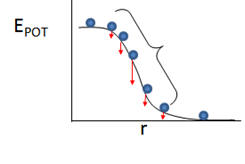
Astute observers will note that the magnitude of the force vector is proportional to the slope.  From this simplistic approach we come to the following equation relating F to E:

The minus sign is required since the force is downward but the energy increases upward.

This simplified approach can be extended into three dimensions, to give the following equation where F is the negative gradient of the potential energy:

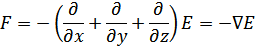
Applying the 1D equation to Hooke’s Law gives

This gives a parabolic graph of E vs displacement.

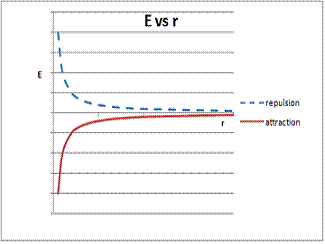
The same approach can be applied to Coulombs Law.  Notice that the result equation for E results in increasingly negative values as r get smaller only when q1 and q2 have opposite charges. 

A graph of E vs r for both attractive and repulsive interactions is shown below. 

Animations of molecular motions in molecular mechanics (accessed 6/3/16)

A 3D energy landscape for the folding of a complicated protein molecule can be found in this link.

In this example, N is the native state at the global energy minimum, U is an unfolded state of a protein, and I is an intermediate state (a local energy minimum).  The black line represents a mechanically-induced unfolding pathway while the red is the trajectory for the folding pathway.  Both have a common intermediate.  Now lets consider molecular mechanics and dynamics in more detail.

Navigation

Return to Molecular Mechanics and Dynamics Contents

Return to Biochemistry Online Table of Contents

Archived version:  Molecular Mechanics and Dynamics