MOLECULAR MECHANICS AND DYNAMICS

04/13/16

E.  Non-Bonded Interaction Energy

The non-bonded energy is calculated for all possible pairs of nonbonded atoms, i and j:

Enonbonding = Σi Σj [ -Bij/rij⁶ +A ij/rij¹² ] + Σi Σj (qi qj) / rij

The first term represents van der Waals interactions while the second terms represents Coloumbic electrostatic interactions.

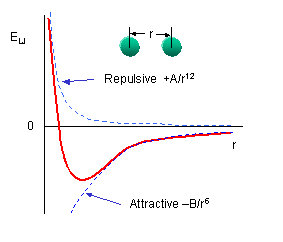
You should remember that van der Waals interactions are short range and occur among all atoms. The 6-12 energy equation based on the Lennard-Jones' potential, shows a negative (attractive) term proportional to -1/r⁶ and a repulsive term proportional to +1/r¹² :

I

The A and B parameters control the depth and position (interatomic distance) of the potential energy well for a given pair of non-bonded interacting atoms (e.g. C:C, O:C, etc.). In effect, A determined the degree of stickiness of the van der Waals attraction, and B determines the degree of hardness of the atoms (e.g. marshmallow-like, billiard ball-like, etc.).

The B parameter is related to the "stickiness" of the interactions and is related to the polarization of the atoms.  B can be obtained from atomic polarizability measurements, or it can be calculated quantum mechanically. The A parameter is empirically derived to fit nonbonded contacts between atoms in crystal structures. 

Wolfram Mathematica CDF Player - Interactive Graph of 6-12 Lennard Jones Potential (free plugin required)

Interactive SageMath Graph: Interactive Graph of 6-12 Lennard Jones Potential

Lennard-Jones Interactive Applet

Couloumb's Law is used to calculate the electrostatic interactions based on appropriate dielectric constants (for buried or water accessible ion-ion pairs).

Enonbonding (electrostatic) =  Σi Σj (qi qj) / rij

A higher dielectric constant reflect more shielding by polar solvents of charge pairs. Partial charges on atoms are calculated using ab initio or semiempirical quantum mechanics.   (usually MOPAC or AMPAC).  The equation for the electrostatic potential is:

Navigation

Return to Molecular Mechanics and Dynamics Contents

Return to Biochemistry Online Table of Contents

Archived version:  Molecular Mechanics and Dynamics