CHAPTER 9 - SIGNAL TRANSDUCTION

E:  Metabolic Control Analysis and Systems Biology  

BIOCHEMISTRY - DR. JAKUBOWSKI

04/16/16

E1. Introduction to Metabolic Control Analysis

Enzyme kinetics may seem difficult given the complicated mathematical derivations, the number of chemical species involved (an enzyme and all its substrates and products), the number of steps in the mechanism, and the large number of rate, kinetic, and dissociation constants. An example of such a “complicated” reaction explored earlier is shown below: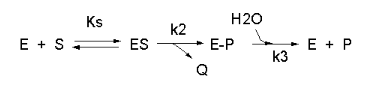

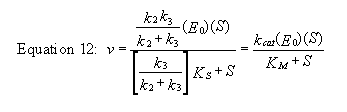
But single enzymes rarely act in isolation. They are components of complex pathways which have a multitude of steps, many of which are regulated. To fully understand a reaction, it is important to study the concentrations of all species in the entire pathway as a function of time. Imagine deriving the equations and determining all the relevant concentrations and constants of a pathway such as glycolysis!

To study enzyme kinetics in the lab, you have to spend much time in developing assays to measure how the concentration of species changes as a function of time to be able to measure the initial velocities of an enzyme-catalyzed reaction. However, in networks of connected metabolic reactions, the concentration of some species in the system may not change. How can this happen? Two simple examples might help explain how.

Example 1: There is zero input or output from a given reaction. This would occur in a closed system for a reversible reaction at equilibrium.

For a reversible reaction of reactant R going to product P with forward and reverse first order rate constants, the following equation can be written at equilibrium:

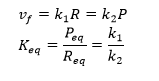
At equilibrium, R and P don’t change.

Example 2:  Consider the reaction as part of a pathway of reactions (like an open system). Now imagine a nonzero input to form reactant R and a nonzero output that consumes product P. If the input and output rates are the same, the concentrations of R and P would not change with time. That is the rate of formation of a reactant R for a given reaction is equal to the rate at which the product P of the give reaction is used. This would lead to a steady state but not equilibrium concentration of the species.

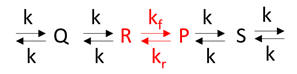
Understanding a pure enzyme in vitro and in vivo requires different approaches. Biochemists like to isolate and purify to homogeneity an enzyme found in some tissue and study its mechanism of action. In doing thermodynamic measurements to measure equilibrium constants (K_eq) or dissociation constants (K_D), from which ΔG⁰ can be calculated, a protein concentration is usually held constant as the binding ligand concentration is varied (independent variable). A dependent variable signal (often spectroscopic) is measured. Measurements are made when equilibrium is reached.

For enzyme kinetic measurements in vitro, the enzyme concentration is usually held constant while substrate and modifiers are varied (independent variables) to determine how velocity (dependent variable) changes. The velocity is determined by the substrate concentration. When inhibition is studied, the substrate is varied while the inhibitor is held constant at several different fixed concentrations.

 In vivo, the substrate concentration and even the enzyme concentration are determined by the velocity. Again compare this to in vitro kinetics when concentrations determine the velocity
For sets of reactions in pathways, it is better to use the term flux, J. In the steady state, the in and out fluxes for a given reaction are identical. Flux J is used to describe the rate of the system whereas rate or velocity v to used describe the rate of an individual enzyme in a system.

Computer programs can find steady states concentrations by finding the roots of the ordinary differential equations (ODE) when set to zero (v_f = v_r). To model a process at very low concentrations, programs can also use probabilistic or stochastic simulations to model probability distributions for species and their change with time for a finite number of particles. In such simulations, concentrations (mM) are placed with number of particles. ODEs don’t work well to describe these conditions since changes in concentrations are not continuous.

Now back to our earlier rhetorical question of deriving the equations and determining all the relevant concentrations and constants of a pathway such as glycolysis! It actually has been done by Teusink et al for glycolysis in yeast. In fact, many such complicated metabolic and signal transduction pathways have been mathematically modeled in the hopes of better understanding cellular and organismal responses. Quantitatively modeling and predicting input, outputs, and concentrations of all species in complex pathways is the basis of systems biology.

Navigation

Return to Chapter 9E:  Metabolic Control Analysis and Systems Biology Sections

Return to Biochemistry Online Table of Contents