CHAPTER 9 - SIGNAL TRANSDUCTION

E:  Metabolic Control Analysis and Systems Biology  

BIOCHEMISTRY - DR. JAKUBOWSKI

04/16/16

E3. Metabolic Control Analysis and Simple Enzyme Inhibition

Biochemists model complex enzyme-catalyzed reactions in the presence and absence of modifiers (either activators or inhibitors) to develop mechanisms for the reactions. The following kinetic parameters are experimentally determined by fitting initial velocity (vo) vs substrate concentration ([S]) through nonlinear fitting algorithms.

• K_m – the Michaelis Constant, the concentration of substrate at half-maximal velocity;
• V_m – the velocity at saturating substrate concentration;
• k_cat - the turnover number for conversion of bound reactant to product;
• K_ix – inhibition dissociation constants.

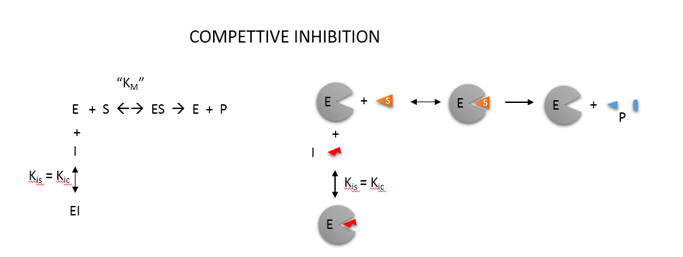
An example of competitive inhibition illustrates a common type of analysis for such reactions.

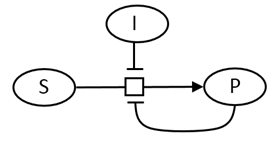
A modern pictorial depiction of a simple irreversible, enzyme-catalyzed reaction of substrate S going to product P with inhibition by the product and by an added inhibitor is shown below:

Consider the simple enzyme-catalyzed reaction for a reversible conversion of substrate S to product P that has 3 reversible steps.

If the forward (f) and reverse (r) chemical reaction steps (reactions 2 and -2) were irreversible and written separately, simple Michaelis-Menten equations could be written for each

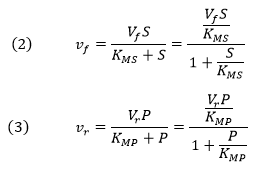
For the actual reversible reactions for step 2, the net forward rate cannot be found by simple subtraction of the two equations above as the differential equations describing the simple forward and reverse rates don’t account for the reverse steps

A simple derivation (assuming rapid equilibrium for both forward and reverse steps) can be made for the net forward reaction. Again consider the following enzyme catalyzed reaction:

You may remember that for the isolated E + S <----> ES and for E + P <----> EP reactions, the simple dissociation constants, K_S and K_P are given by

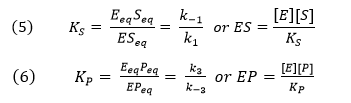
The rapid equilibrium assumption states that the rate of dissociation of ES and EP, which are both physical steps, are much faster than the rate of the chemical conversion steps for each complex. Hence k-1 >> k2 and k3 >> k-2, so the relative amounts of ES and EP can be determined from the dissociation constants as shown above.

Mass conservation of enzyme gives

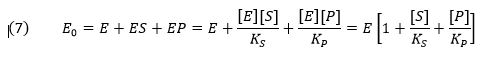
From this we can get the fractional amount of both ES and EP

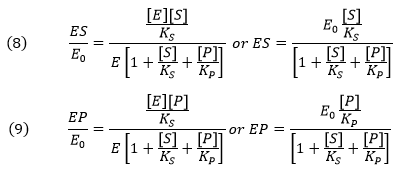
Now we can derive the rate equation for the net forward reaction for the rapid equilibrium case:

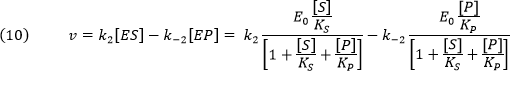
Knowing that k₂E₀ and k_-2E₀ represent the maximal velocities, V_f and V_r, respectively, the equation becomes:

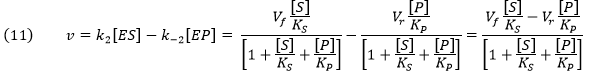
An equation of similar form can be derived from the steady state assumption. This equation is clearly different from the earlier equation (4) derived by intuitively assuming a simple subtraction of the irreversible forward and reverse rates which we have now shown to be invalid by comparison.

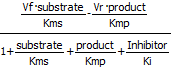
Programs like COPASI have many built in equations for velocities of many enzyme-catalyzed reactions that have similar forms. Two are shown below:

Reversible Michaelis-Menten: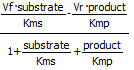

Competitive Inhibition Reversible:

Navigation

Return to Chapter 9E:  Metabolic Control Analysis and Systems Biology Sections

Return to Biochemistry Online Table of Contents