CHAPTER 9 - SIGNAL TRANSDUCTION

E:  Metabolic Control Analysis and Systems Biology  

BIOCHEMISTRY - DR. JAKUBOWSKI

04/16/16

E5. Concentration Control and Elasticity Coefficients

The Concentration control coefficient (C^S_Ei), a global property of the system, gives the relative fractional change in metabolite concentration S_j (dS_j/S_j), where S_j is the concentration of any metabolite in the system and as such is a system variable, with fractional change in concentration or activity of enzyme E_i (du_i/u_i). Similar equations as above apply.

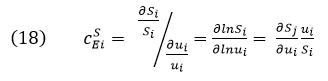
It can be shown that the sum of all of the individual C^S_Ei = 0 (another summation theorem), not 1 as in the case of flux control coefficients. This again would make sense in the steady state. Flux coefficients usually vary from 0 to 1, but concentration coefficients can vary from negative to positive and small to large.

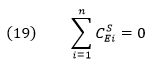
The concentration control coefficients can have large values as seen from a simple example. For a given enzyme, at low [S], for example when [S] << Km,

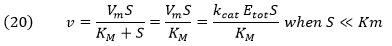
If the enzyme had only 0.1x of its normal activity (due to a mutation for example), then to maintain constant flux, the [S] would have to increase 10 fold.

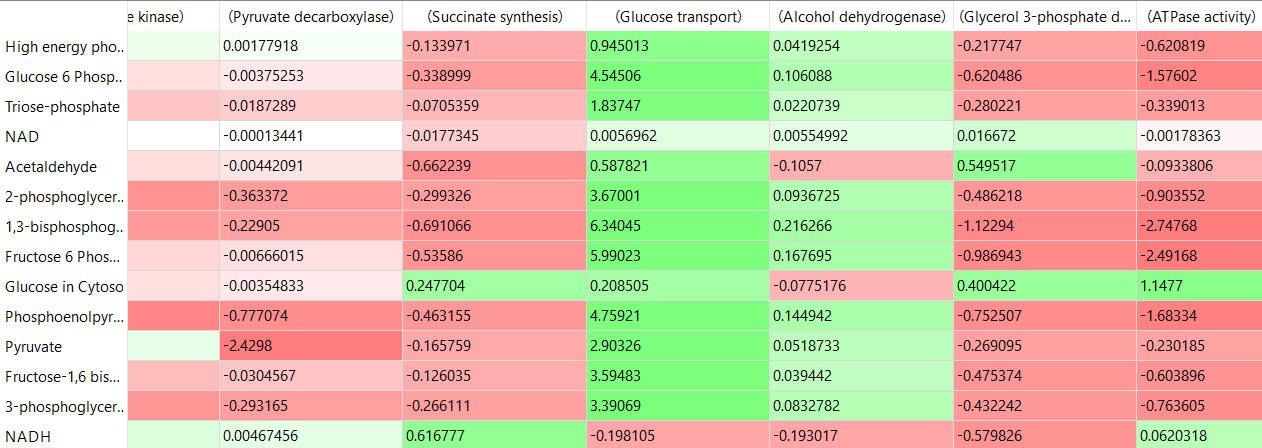
The tables below shows the C^S_Ei values for incremental changes in substrate (1%).  

table, part 2:

table, part 3

The Elasticity Coefficient, in contrast to the flux and concentration control coefficients, which are properties of the system, is a local property and can be measured using isolated enzyme and substrate. It makes sense that some kinetic property of the isolated enzyme would affect its propensity to affect system flux.

The elasticity coefficient gives a measure of how much a substrate S (or other substance) can change the reaction rate (v) of an isolated enzyme. (Note we use v and not flux J, which describes a system property.) Hence

Hence the elasticity coefficient can be determined using basic enzyme kinetics of the isolated enzyme. Note that the coefficient at each S concentration is the slope of the v vs S curve multiplied by the S/v at that tangent point. The elasticity coefficient must be evaluated at the same concentration of enzyme and substrate as found in vivo in the steady state. Velocity (v), not flux, is used. In the above case, S is substrate, but it could be product or modifier. There is a different elasticity coefficient for each parameter. There is no summation theory for elasticities. Values can be positive for species that increase the velocity or negative for those that decrease it. Hence there can be multiple elasticities.

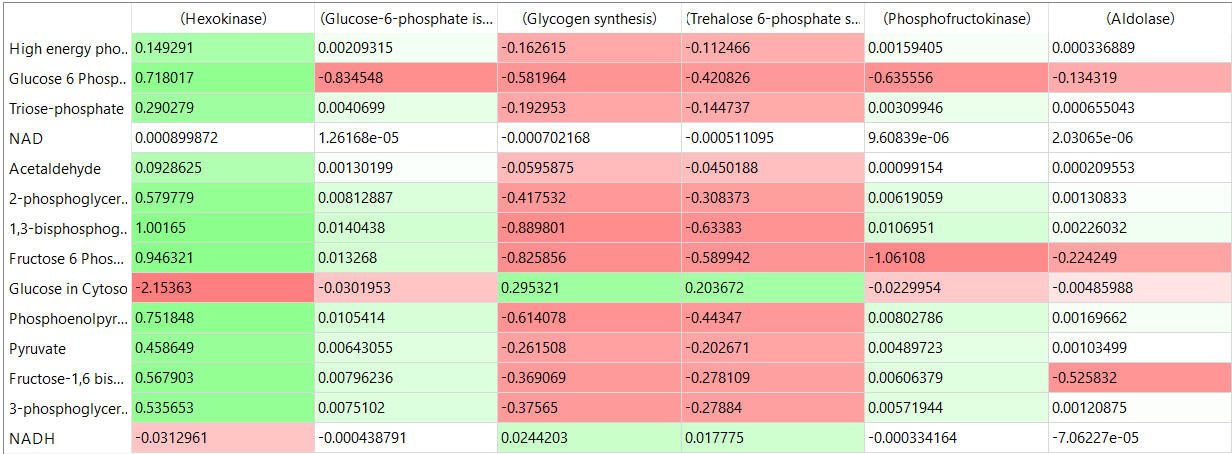
The tables below show the elasticity coefficients (relative or scaled) for yeast glycolysis determined using COPASI.

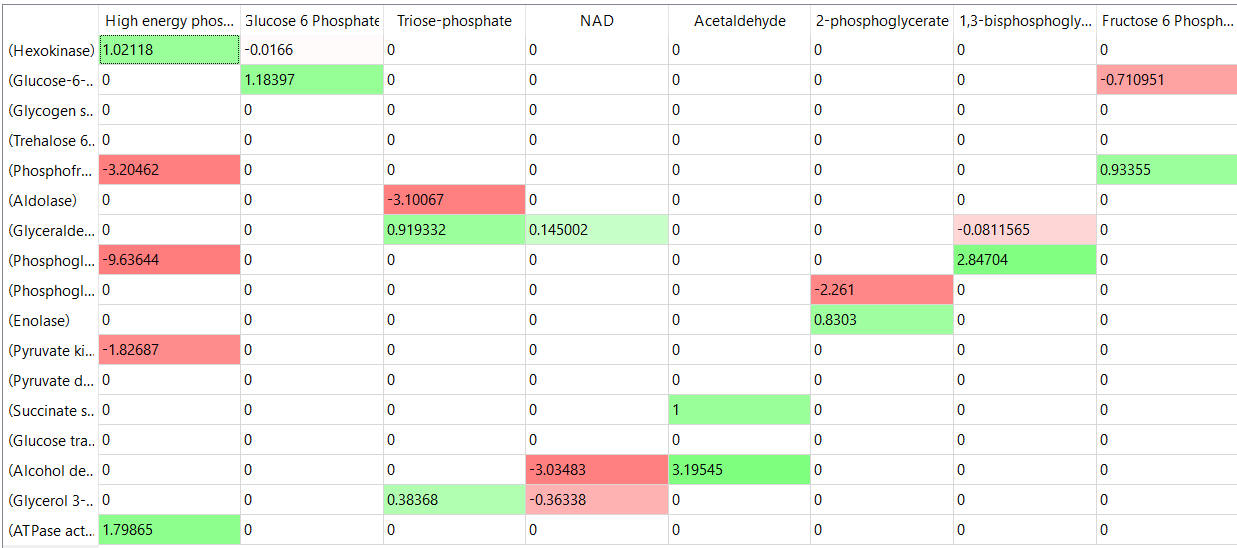
table, part 2

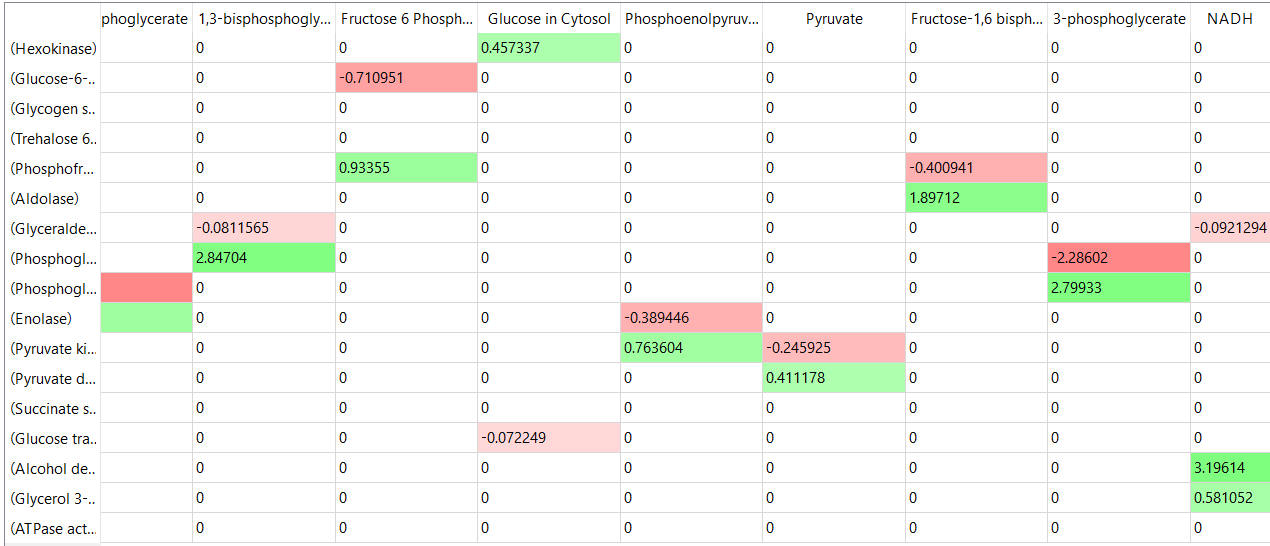
Thinks to note:

• the columns show substrates not enzymes;
• green cells (with positive elasticities) are generally for substrates for their target enzymes (for example, glucose-6-phosphate for phosphoglucomutase);

Other "generic" sensitivities can be determined as well.  For example, minor (Incremental) changes in Km, Vm, or Kix for specific enzymes could affect fluxes in a pathway.  

A link between system control coefficients and local coefficients:

You would think that there should be some relationship between a system variable such as the flux control coefficient and a local variable such as the elasticity coefficient? There is and it is expressed by the Connectivity Theorem (below). If a substrate S is acted upon by many different enzymes (i …… n), which is very likely especially for branch points in metabolic pathways, then it can be shown that

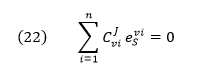
Navigation

Return to Chapter 9E:  Metabolic Control Analysis and Systems Biology Sections

Return to Biochemistry Online Table of Contents