CHAPTER 6 - TRANSPORT AND KINETICS 

 
B:  Kinetics of Simple and Enzyme-Catalyzed Reactions

BIOCHEMISTRY - DR. JAKUBOWSKI

4/10/16

B3.   Rapid Equilibrium Enzyme-Catalyzed Reactions

We have previously derived equations for the reversible binding of a ligand to a macromolecule. Next we derived equations for the receptor-mediated facilitated transport of a molecule through a semipermeable membrane. This latter case extended the former case by the addition of a physical transport step. Now, in what hopefully will seem like d�j� vu, we will derive almost identical equations for the chemical transformation of a ligand, commonly referred to as a substrate, by an enzyme. Two scenarios will be studied.

1. Rapid Equilibrium Assumption - enzyme E (macromolecule) and substrate S (ligand) concentrations can be determined using the dissociation constant since E, S, and ES are in rapid equilibrium, as we previously used in our derivation of the equations for facilitated transport.   Sorry about the switch from A to S in designation of substrate. Biochemists use S to represent the substrate (ligand) but also use A, B, and P and Q to represent reactant and products in the case of multi-substrate and multi-product reactions.
2. Steady State Assumption (more general) -  enzyme and substrate concentrations are not those determined using the dissociation constant.

Enzyme kinetics experiments, as we will see in the next several chapters, must be used to determine the detailed mechanism of the catalyzed reaction.  Using kinetics analyzes you can determine the order of binding/dissociation of substrates and products, the rate constants for individual steps, and clues as the to methods used by the enzyme in catalysis.

Consider the following reaction mechanism for the enzyme-catalyzed conversion of substrate S into product P. (We will assume that the catalyzed rate is much greater than the noncatalyzed rate.)

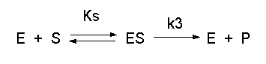
As we did for the derivation of the equations for the facilitated transport reactions under rapid equilibrium conditions, this derivation is based on the assumption that the relative concentrations of S, E, and ES can be determined by the dissociation constant, Ks, for the interactions and the concentrations of each species during the early part of the reaction (i.e. under initial rate conditions). Assume also the S >> Eo.  Remember that under these conditions, S does not change much with time. Is this a valid assumption?  Examine the mechanism shown above.  S binds to E with a second order rate constant k1.  ES has two fates. It can dissociate with a first order rate constant k2 to S + E, or it can be converted to product with a first order rate constant of k3 to give P + E. If we assume that k2 >> k3 (i.e. that the complex falls apart much more quickly than S is converted to P), then the relative ratios of S, E, and ES can be described by Ks. Alternatively, you can think about it this way. If S binds to E, most of S will dissociate, and a small amount will be converted to P. If it does, then E is now free, and will quickly bind S and reequilibrate since the most likely fate of bound S is to dissociate, not be converted to P (since k3 << k2). This make sense also, if you consider that the physical step characterized by k2 is likely to be quicker than the chemical step, characterized by k3. Hence the following assumptions have been used:

• S >> Eo
• Po = 0
• k3 is rate limiting (i.e. the slow step)

 We would like to derive equations which show the velocity v as a function of the initial substrate concentration, So , (assuming that P is negligible over the time course of measuring the initial velocity). Also assume that the v catalyzed >> vnoncatalyzed. In contrast to the first-order reaction of S to P in the absence of E, v is not proportional to So but rather to Sbound. as we described in class with facilitated diffusion (flux proportional to AR, not free A). Therefore,

v α ES, or

Equation 1)    v = const [ES] = k3 [ES]

where v is the  velocity.   How can we calculate ES when we know S (which is equal to So) and Etot (which is Eo)? Let us assume that S is much greater than E, as is the likely biological case. We can calculate ES using the following equations and the same procedure we used for the derivation of the binding equation, which gives the equation below:

ES = (EoS)/(Ks + S)   (analogous to ML = (MoL)/(Kd + L) 

DERIVATION

Equation 5)    v = const [ES] = k3 [ES] = k3 EoS/(Ks + S) = VmS/(Ks + S).

This is the world famous Henri-Michaelis-Menten Equation

Just as in the case with noncatalyzed first order decay, it is easiest to measure the initial velocity of the reaction when [S] does not change much with time and the velocity is constant (i.e the slope of the dP/dt curve is constant).   A plot of [P] vs t (called a progress curve) is made for each different substrate concentration studied.   From these curves, the initial rates at each [S] is determined.  Alternatively, one set reaction time is determined for all the different substrates concentrations that gives a linear rise in [P] with time.  At the time, the reaction can be stopped (quenched) with a reagent that does not cause any change in S or P.  Initial rates can be easily calculated for each [S] from a single data point in this case.  i

• a plot of v vs S is hyperbolic
• v = 0 when S = 0
• v is a linear function of S when S<<Ks.
• v = Vmax (or Vm) when S is much greater than Ks
• S = Ks when v = Vmax/2.

These are the same conditions we detailed for our understanding of the binding equation

ML = (MoL)/(Kd + L)

The interactive Mathematics graph below allows you to change the relative value of Vm and Ks (which in the graph is given the more general name of Km).  Note that when Km is not << S, the graph does not reach saturation and does not look hyperbolic.  It should be apparent from the graph that only if S >> Km (or when S is approximately 100x greater than Km) will saturation be achieved.

Wolfram Mathematica CDF Player - Michaelis-Menten Equation (free plugin required)

Interactive SageMath Graph: Michaelis-Menten Equation

Very often these graphs are transformed into double reciprocal or Lineweaver-Burk plots as shown below.  These plots can be used to estimate Vm from the 1/v intercept (1/Vm) and Km from the 1/S axis (-1/Km).  These values should be used as "seed" values for a nonlinear fit to the hyperbola that models the actual v vs D curve.

Interactive SageMath Graph: Lineweaver Burk Plot

• History and Picture of Maude Menten

As we saw in the graph of A or P vs t for a noncatalyzed, first order reaction, the velocity of the reaction, given as the slope of those curves, is always changing.  Which velocity should we use in Equation 5?  The answer invariably is the initial velocity measured in the early part of the reaction when little substrate is depleted.  Hence v vs S curves for enzyme catalyzed reactions invariably are really v0 vs [S].

Navigation

Return to B:  Kinetics of Simple and Enzyme-Catalyzed Reactions Sections

Return to Biochemistry Online Table of Contents

Archived version of full Chapter 5B:  Kinetics of Simple and Enzyme-Catalyzed Reactions