CHAPTER 6 - TRANSPORT AND KINETICS 

 
B:  Kinetics of Simple and Enzyme-Catalyzed Reactions

BIOCHEMISTRY - DR. JAKUBOWSKI

4/10/16

B6.  More Complicated Enzyme-catalyzed Reactions

Not all reactions can be characterized so simply as a simple substrate interacting with an enzyme to form an ES complex, which then turns over to form product. Sometimes, intermediates form. For example, a substrate S might interact with E to form a complex, which then is cleaved to products P and Q. Q is released from the enzyme, but P might stay covalently attached. This happens often in the hydrolytic cleavage of a peptide bond by a protease, when an activated nucleophile like Ser reacts with the sessile peptide bond in a nucleophilic substitution reaction, releasing the amine end of the former peptide bond as the leaving group, while the carboxy end of the peptide bond remains bonded to the Ser as an Ser-acyl intermediate. Water then enters and cleaves the acyl intermediate, freeing the carboxyl end of the original peptide bond. This is shown in the written reaction below:

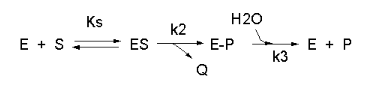
To simplify the derivation of the kinetic equation, let's assume that E, S, and ES are in rapid equilibrium defined by the dissociation constant, Ks. Assume Q has a visible absorbance, so it is easy to monitor.  Assume from the steady state assumption that:

d[E-P]/dt = k2[ES] - k3[E-P] = 0  (assuming k3 is a pseudo first order rate constant and [H2O] doesn't change.

The velocity depends on which step is rate limiting.  If k3<<k2, then the k3 step is rate-limiting.   Then

  v = k3[E-P]

  If k2<<k3, then the k2 step is rate-limiting.  Then

  v = k2[ES]

For a homework assignment, you derived the following kinetic equation for this reaction, assuming  v = k2[ES].

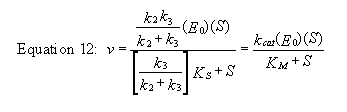
You can verify that you get the same equation if you assume that v = k3[E-P].  (Also, kcat will be defined below.)

This equation looks quite complicated, especially if you substitute for Ks, k-1/k1. All the kinetic constants can be expressed as functions of the individual rate constants. However this equation can be simplified by realizing the following:

• When S >> [Ks(k3)/(k2+k3)], v = [(k2k3)/(k2 + k3)]Eo = Vm
• [Ks(k3)/(k2+k3)] = constant = Km

Substituting these into equation 7 gives:

Equation 13)   v = Vm(S)/(Km+ S)

This again is the general form of the Michaelis-Menten equation

Note in the first bulleted item above that for this reaction, Vm = [(k2k3)/(k2 + k3)]Eo

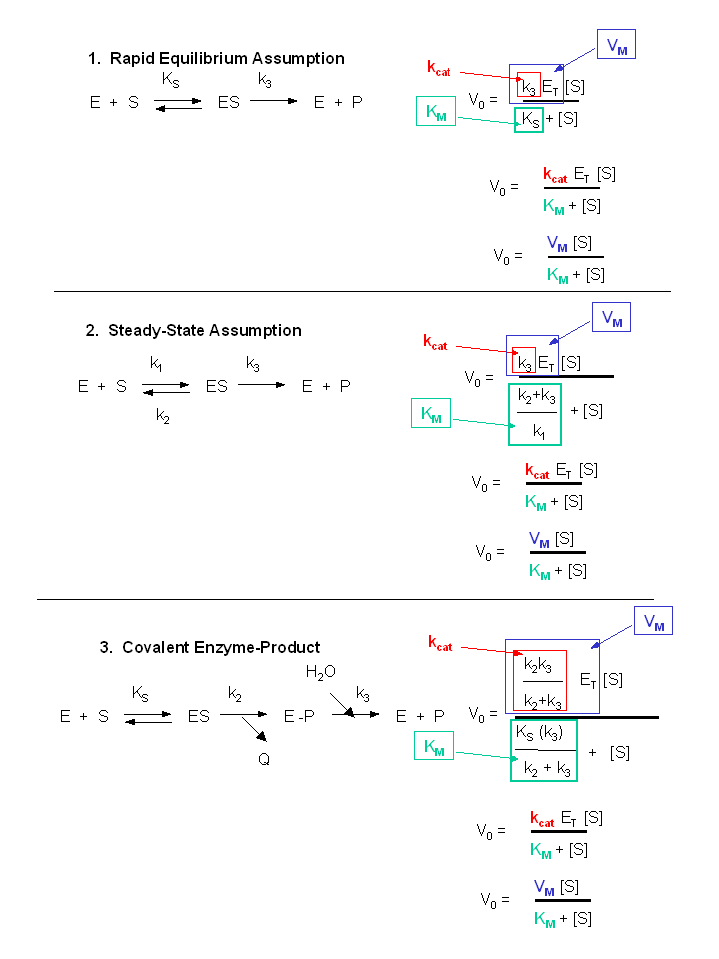
This is more complicated than our earlier definition of Vm = k3Eo. They are similar in that the term Eo is multiplied by a constant which is itself a function of rate constant(s). The rate constants are generally lumped together into a generic constant called kcat. For the simple reaction kcat = k3 but for the more complicated reaction with a covalent intermdiate which we just deived, kcat = (k2k3)/(k2 + k3). For all reactions,

Equation 14)   Vm = kcatEo.

Figure:  Summary of vo vs S equations - Meanings of Km, kcat and Vm.

Navigation

Return to B:  Kinetics of Simple and Enzyme-Catalyzed Reactions Sections

Return to Biochemistry Online Table of Contents

Archived version of full Chapter 5B:  Kinetics of Simple and Enzyme-Catalyzed Reactions