Biochemistry Online: An Approach Based on Chemical Logic

CHAPTER 6 - TRANSPORT AND KINETICS

C: ENZYME INHIBITION

BIOCHEMISTRY - DR. JAKUBOWSKI

06/12/2014

Learning Goals/Objectives for Chapter 6C: After class and this reading, students will be able to

differentiate among competitive, uncompetitive, and mixed inhibition of enzymes by reversible, noncovalent inhibitors by writing coupled chemical equilibria equations and drawing cartoons showing molecular interactions among, E, S, and I;
using LeChatelier's principle and coupled chemical equilibria equations, draw double reciprocal (Lineweaver-Burk plots) and semilog plots for enzyme catalyzed reactions in the presence of different fixed concentrations of inhibitors and activators of enzyme
define KIS and KII for competitive, uncompetitive, and mixed inhibition from coupled chemical equilibria and double reciprocal plots;
differentiate between apparent and actual dissociations constants constants of an inhibitor and enzyme from double reciprocal plots and equations initial rate mathematical equations;
define agonist, partial agonist, antagonist, and mixed (noncompetitive antagonists) from analogy to enzymes and their inhibitors;
describe different ways that pH changes could affect the activity of an enzyme and suggest how each could affect Km and kcat.

C3. Uncompetitive Inhibition

Reversible uncompetitive inhibition occurs when I binds only to ES and not free E. One can hypothesize that on binding S, a conformational change in E occurs which presents a binding site for I. Inhibition occurs since ESI can not form product. It is a dead end complex which has only one fate, to return to ES. This is illustrated in the chemical equations and molecular cartoon below.

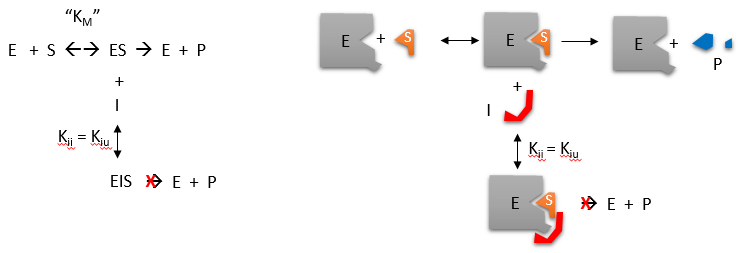
uncompinhib

Let us assume for ease of equation derivation that I binds reversibly to ES with a dissociation constant K_ii. The second "i" in the subscript "ii" indicates that the intercept of the 1/v vs 1/S Lineweaver-Burk plot changes while the slope stays constant. Kii is also named K_iu, where the subscript "u" stands for the uncompetitive inhibition constant.

A look at the top mechanism shows that in the presence of I, as S increases to infinity, not all of E is converted to ES. That is, there is a finite amount of ESI, even at infinite S. Now remember that Vm = kcatEo if and only if all E is in the form ES . Under these conditions, the apparent Vm, Vmapp is less than the real Vm without inhibitor. In addition, the apparent Km, Kmapp, will change. We can use LaChatelier's principle to understand this. If I binds to ES alone, and not E, it will shift the equilibrium of E + S <==> ES to the right , which would have the affect of decreasing the Kmapp (i.e. it would appear that the affinity of E and S has increased.). The double reciprocal plot (Lineweaver Burk plot) offers a great way to visualize the inhibition. In the presence of I, both Vm and Km decrease. Therefore, -1/Km, the x-intercept on the plot, will get more negative, and 1/Vm will get more positive. It turns out that they change to the same extent. Therefore the plots will consist of a series of parallel lines, which is the hallmark of uncompetitive inhibition.

uncompinhib2

An equation, shown in the diagram above, can be derived which shows the effect of the uncompetitive inhibitor on the velocity of the reaction. The only change is that the S term in the denominator is multiplied by the factor 1+I/Kii. We would like to rearrange this equation to show how Km and Vm are affected by the inhibitor, not S, which obviously isn't. Rearranging the equation as shown above shows that Kmapp = Km/(1+I/Kii) and Vmapp = Vm/(1+I/Kii). This shows that the apparent Km and Vm do decrease as we predicted. Kii is the inhibitor dissociation constant in which the inhibitor affects the intercept of the double reciprocal plot. Note that if I is zero, Km and Vm are unchanged.