CHAPTER 6 - TRANSPORT AND KINETICS

C: ENZYME INHIBITION

BIOCHEMISTRY - DR. JAKUBOWSKI

06/12/2014

C4. Noncompetitive and Mixed Inhibition

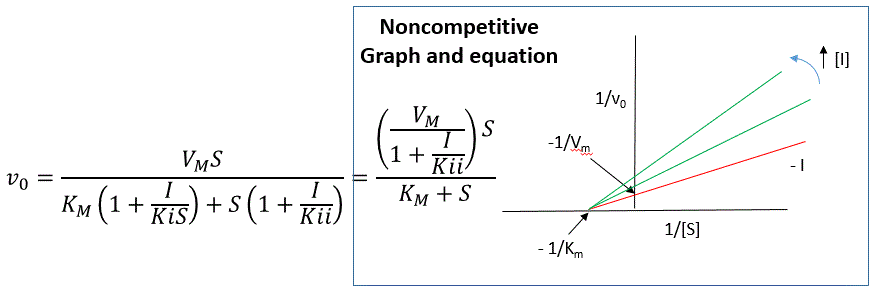
Reversible noncompetitive inhibition occurs when I binds to both E and ES. We will look at only the special case in which the dissociation constants of I for E and ES are the same. This is called noncompetiive inhibition. It is quite rare as it would be difficult to imagine a large inhibitor which inhibits the turnover of bound substrate having no effect on binding of S to E.  However covalent interaction of protons with both E and ES can lead to noncompetitive inhibition.   In the more general case, the Kd's are different, and the inhibition is called mixed. Since inhibition occurs, we will hypothesize that ESI can not form product. It is a dead end complex which has only one fate, to return to ES or EI. This is illustrated in the chemical equations and in the molecular cartoon below.

Let us assume for ease of equation derivation that I binds reversibly to E with a dissociation constant of Kis (as we denoted for competitive inhibition) and to ES with a dissociation constant Kii (as we noted for uncompetitive inhibition). Assume for noncompetitive inhibition that Kis = Kii. A look at the top mechanism shows that in the presence of I, as S increases to infinity, not all of E is converted to ES. That is, there is a finite amount of ESI, even at infinite S. Now remember that Vm = kcatEo if and only if all E is in the form ES . Under these conditions, the apparent Vm, Vmapp is less than the real Vm without inhibitor. In contrast, the  apparent Km, Kmapp, will not change since I binds to both E and ES with the same affinity, and hence will not perturb that equilibrium, as deduced from LaChatelier's principle. The double reciprocal plot (Lineweaver Burk plot) offers a great way to visualize the inhibition. In the presence of I, just Vm will decrease. Therefore, -1/Km, the x-intercept will stay the same, and 1/Vm will get more positive. Therefore the plots will consists of a series of lines intersecting on the x axis, which is the hallmark of noncompetitive inhibition. You should be able to figure out how the plots would appear if Kis is different from Kii (mixed inhibition).
An equation, shown in the diagram above can be derived which shows the effect of the noncompetitive inhibitor on the velocity of the reaction. In the denominator, Km is multiplied by 1+I/Kis, and S by 1+I/Kii. We would like to rearrange this equation to show how Km and Vm are affected by the inhibitor, not S, which obviously isn't. Rearranging the equation as shown above shows that Kmapp = Km(1+I/Kis)/(1+I/Kii) = Km when Kis=Kii, and Vmapp = Vm/(1+I/Kii).  This shows that the Km is unchanged and Vm decreases as we predicted. The plot shows a series of lines intersecting on the x axis. Both the slope and the y intercept are changed, which are reflected in the names of the two dissociation constants, Kis and Kii. Note that if I is zero, Kmapp = Km and Vmapp = Vm.  Sometimes the Kis and Kii inhibition dissociations constants are referred to as Kc and Ku (competitive and uncompetitive inhibition dissociation constants.

Mixed (and non-)competitive inhibition (as shown by mechanism above) differ from competitive and uncompetiive inhibition in that the inhibitor binding is not simply a dead end reaction in which the inhibitor can only dissociate in a single reverse step.  In the above equilibrium, S can dissociate from ESI to form EI so the system may not be at equilibrium. With dead end steps, no flux of reactants occurs through the dead end complex so the equilibrium for the dead end step is not perturbed. 

Other mechanisms can commonly give mixed inhibition.  For example, the product released in a ping pong mechanism (discussed in the next chapter) can give mixed inhibition.

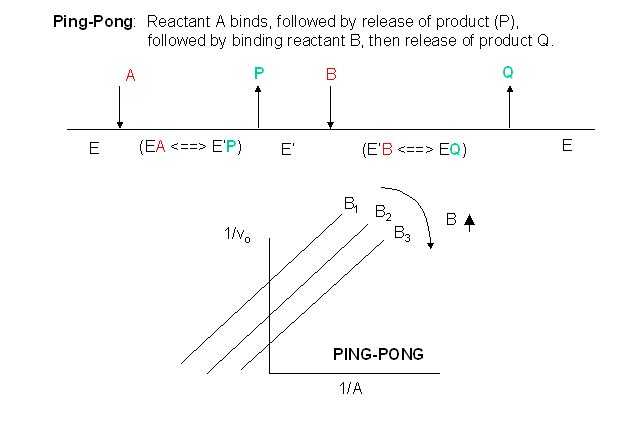
If P, acting as a product inhibitor, can bind to two different forms of the enzyme (E' and also E), it will act as an mixed inhibitor.

Java Applet:  Noncompetitive Inhibition

4/26/13Wolfram Mathematica CDF Player - Mixed Inhibition v vs S curves; Kis and Kii called Kc and Ku (start sliders at high values) (free plugin required)

Interactive SageMath MIxed Inhibition

4/26/13Wolfram Mathematica CDF Player - Lineweaver-Burk plots for Mixed Inhibition v vs S curves (start sliders at high values) (free plugin required). Note where the inhibited and inhibited curves intersect at different values of Kis and Kii (in the graph termed Kc and Ku).  When Kis = Kii, the inhibition is noncompetitive.

Interactive SageMath Mixed Inhibition (Red graph + Inhibitor, Blue graph - Inhibitor, Green Axes

If you can apply LeChatilier's principle, you should be able to draw the Lineweaver-Burk plots for any scenario of inhibition or even the opposite case, enzyme activation!

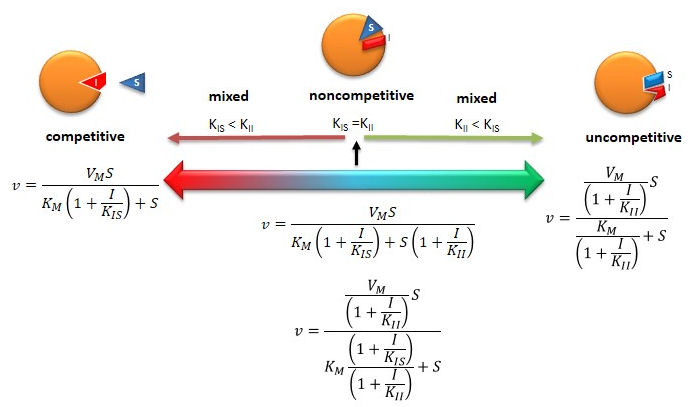
Figure:  Summary of Reversible Enzyme Inhibition

Navigation

Return to Chapter 6C:  Enzyme Inhibition Sections

Return to Biochemistry Online Table of Contents

Archived version of full Chapter 6C:  Enzyme Inhibition