CHAPTER 6 - TRANSPORT AND KINETICS

C: ENZYME INHIBITION

BIOCHEMISTRY - DR. JAKUBOWSKI

06/12/2014

C5.  Enzyme Inhibition in Vivo

The whole pharmaceutical industrial is devoted to finding drug molecules that affect biological processes.  Usually this means the development of small molecule inhibitors of target proteins, although recent work has expanded to development of inhibitory RNA molecules that affect DNA transcription and mRNA translation.  Using combinatorial synthetic techniques and computational modeling, it has gotten easier to develop small molecule inhibitors (especially competitive ones) that inhibit proteins in vitro using purified enzymes, substrates, and inhibitors in lab testing.  Assuming that the inhibitor could pass through the membrane and accumulate to a sufficient enough concentration, would it have the same inhibitory properties in the cell as in the test tube?  The answer turns out to be maybe.   Remember that a cell is tightly packed with a multitude of other small molecules and macromolecules.  In addition, the enzyme targeted for inhibition is most likely in part of a pathway of enzymes that feeds reactant into the enzyme and removes the product.  Hence the flux of substrate and product is controlled by the entire pathway and not just the single target enzyme although the product concentration of the target  enzyme  is determined by kinetic parameters for the enzyme and available substrate concentration. .

The conditions under which the enzymes are studied (in vitro) and operate (in vivo) are very different. 

• In vitro (in the lab), the enzyme is held at a constant concentration while the substrate is varied (i.e the substrate concentration is the independent variable).  The velocity is determined by the substrate concentration.  When inhibition is studied, the substrate is varied while the inhibitor is held constant at several different fixed concentrations. 

• In vivo (in the cell), the velocity might be held at a relatively fixed level with the substrate determined by the velocity.  To avoid a bottleneck in flux, substrate can't build up at the enzyme, so the enzyme processes it in a steady state fashion to produce product as determined by the Michael-Menten equation.

What happens when an inhibitor is added in vivo?  Let's assume that the enzyme is running at v = Vm/2.  We saw before for in vitro inhibition that it is sometimes difficult to differentiate competitive and uncompetiive inhibition (as evidenced from real, not hypothetical perfect double reciprocal plots).  How might in vivo inhibition plots look at constant velocity (for example v=Vm/2) when both I and S can vary and in which S for an enzyme in the middle of a pathway is determined by v?

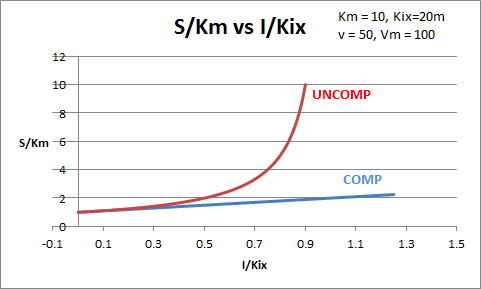
The equations and graph below shows the ratio of S/Km vs I/Kix for inhibition at constant v, a condition encountered when an enzyme in a metabolic pathways is subject to flux controls imposed by the entire pathway.  The x axis reflects the relative amount of inhibitor compared to its inhibition constant.    Likewise the y axis reflects the relative amount of substrate compared to its Km.  The graph for in vivo competitive inhibition is linear, but it "blows up" for uncompetitive inhibition.

Figure:  Competitive and Uncompetitive Inhibition in vivo

Competitive Inhibition at Contant v		Uncompetitive Inhibition at Contant v

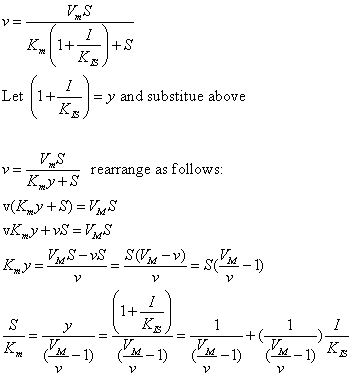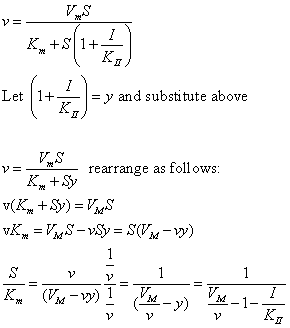These graphs and associated equations are dramatically different from the very similar forms of inhibition equations and curves for in vitro inhibition at varying S and different fixed values of inhibitor.  Consider the uncompetitive graph and equation. In the absence of inhibitor, if S=Km, then Vm/v = 2 and, of course, the calculated value from the equation above of S/Km = 1. If I is allowed to increase to a value of Kii, again at constant v=Vm/2, then the right hand side goes to infinity. 

In a linked series of reaction, if the middle reaction is inhibited, the substrate for that enzyme builds, whether the inhibition is competitive or uncompetitive. With competitive inhibition, the substrate concentration can be raised to meet the requirements of the enzyme.  But as the above figure shows, this can't happen for uncompetitive inhibition since as more substrate accumulates, the reaction reaches a point where the steady state is lost.

Obviously, this limiting case can't be realistically reached but it does suggest that uncompetitive inhibitors would be more effective in vivo in controlling a metabolic pathway than competitive inhibitors.  Cornish-Bowden argues that purely uncompetitive inhibitors are rare in nature because of the degree of inhibition they can hypothetical produce (1986).  Likewise he suggests that medicinal chemists should synthesize uncompetitive inhibitors if their goal is to maximally inhibit a metabolic pathway under the kind of flux control described above.  Although it is more difficult to synthesis a purely uncompetitive inhibitor (as it can't be modeled after the structure of a natural ligand that bind to the active site and are competitive inhibitors, he notes synthesizing mixed (and noncompetitive) inhibitors whose Kii values are of reasonable size compared to their Kis values, would be one approach to try.

Navigation

Return to Chapter 6C:  Enzyme Inhibition Sections

Return to Biochemistry Online Table of Contents

Archived version of full Chapter 6C:  Enzyme Inhibition