Biochemistry Online: An Approach Based on Chemical Logic

CHAPTER 2 - PROTEIN STRUCTURE
F: THERMODYNAMICS AND IMFs IN PROTEIN STABILITY
BIOCHEMISTRY - DR. JAKUBOWSKI
Last Update: 3/2/16
|
Learning Goals/Objectives for Chapter 2F: After class and this reading, students will be able to ...
|
"You could not step twice into the same river" - Heraclitus of Ephesus (c.535 BC - 475 BC)
F1. Introduction to Protein Stability
This material is not easy, and is perhaps the most intellectually challenging of the entire book. Most of this review comes from an article by Ken Dill, Biochemistry, 29, 7133-7155 (1990). A more recent reanalysis that comes to a significantly different conclusion with respect to the role of H bonds in protein folding and stability, written by Pace, Biochemistry. 40, pg 310 (2001), is discussed at the end.
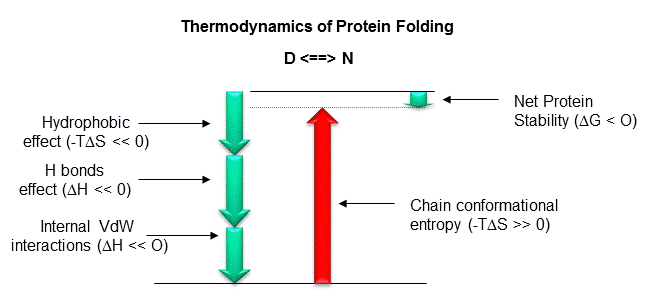
To summarize, it now appears that both the hydrophobic effect and H bonds appear to drive protein folding and promote protein stability. Extrapolating from the results of studies of the transfer of small model H bond donors/acceptors and hydrophobic molecules from water to nonpolar solvents, it would appears that H bond interactions (as well as ion ..ion interactions) do not drive protein folding per se. Rather, the biggest contributors to stabilization of the native state are the hydrophobic effect and the van der Waals interactions among the tightly packed buried atoms of the protein. However, from recent studies (Pace) of mutant proteins made through site-specific mutagenesis, it appears that H bonds contribute significantly to protein folding and stability, and may make a greater contribution to stability of the native state than the hydrophobic effect. The main factor which opposes folding is chain conformational entropy. These positive and negative factors sum up to a small negative DG favoring protein folding, implying marginal stability of the native protein at normal temperatures.
What types of intermolecular forces might act within a protein and between proteins and solvent molecules that would cause a protein to fold spontaneously to a unique 3D structure? These forces can be long range (ion-ion, ion dipole, or dipole-dipole) or short range (van der Waals repulsive and attractive forces). The interactions can be local (between adjacent amino acids in the linear sequence) or nonlocal (between sequences separated in the linear sequence but brought close together in 3D space). Clues as to what stabilizes the tertiary structure of a native protein can be gained by subjecting proteins to agents that unfold or denature a protein. Such agents include extremes of pH, high concentrations of some salt solutions or organic solvents, and temperature extremes. Such experiments show that native proteins are only marginally stable (about 0.4 kJ/mol amino acid - or around - 10 kcal/mol for a protein of molecular weight of 10,000 - about 100 amino acids). We will consider the different types of intermolecular forces (ion-ion, H bonds, van der Waals, and the hydrophobic effect) individually and ask if each is a significant driving force for protein folding.
Figure: Diagram showing relative contributions to the DG for protein folding.
Most of this chapter will deal with H bonding and the hydrophobic effect. A theme of any biochemistry course is that if you can understand the interactions among small molecules, you can apply that knowledge to the understanding of larger molecules like proteins. To understand if H bonds within proteins, often buried in the more hydrophobic interior of the protein, drive protein folding, we will first examine the thermodynamics of H bond formation of a small molecule, N-methylacetamide, in water and in a nonpolar solvent. To understand if the hydrophobic effect, mediated by burying of nonpolar side chains within the more nonpolar center of the protein, drives protein folding, we will examine the thermodynamics of benzene solubility in water. Most recent studies involve the creation of specific mutants at amino acid position that might reveal the contributions of H bonding and the hydrophobic effect to folding and protein stability.
F2. Ion - Ion Interactions
These could be investigated by altering pH or ionic strength. Why is that?
a. General Charge Interactions - Proteins denature at extremes of pH. At these extremes, proteins have a maximal positive or negative charge, as evident in graphs which show denaturation temperature vs pH for proteins.
Figure: Denaturation temperature vs pH for proteins
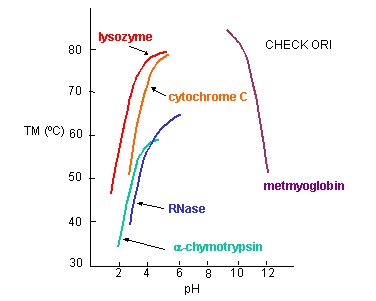
Under extremes of pH (but not so great as to catalyze peptide bond cleavage, electrostatic repulsions would cause the protein to denature. The folded, compact state has an increasing charge density at pH extremes, which could be alleviated by unfolding to a less dense state. But what about specific charge pair interactions? In contrast to the general charge interactions, these might actually stabilize a protein. Are they the predominant factor that determines stability?
b. Specific Charge Interactions (charge pairs) - If ion pairs are the source of protein stability, you would expect that high salt could disrupt them, and lead to denaturation. Although some salts do denature proteins, other stabilize them. Other evidence argues against this idea. Ion pairs are not conserved in evolution. In addition, the number of ion pairs in proteins is small (approx. 5/150 residues, with one of those buried). Also, the stability of a protein shows little dependence on pH or salt concentration (at low concentrations) near the isoelectric point, the pH at which proteins have a net zero charge.
The overall charge state affects not only the stability of a protein but also its solubility. Proteins are most insoluble at their isoelectric point since at that pH (where they have a net 0 charge) the proteins experience the least electrostatic repulsion and are most likely to aggregate and precipitate. Low salt concentration also promotes insolubility. Mutagenesis studies show that solubility can be increased by replacing nonpolar groups on the surface with polar ones. Pace (2009) cites studies on RNase Sa which has a maximally exposed Thr 76. If it is replaced with Asp, the solubility increased to 43 mg/ml but if it is replaced with Trp, it decreased to 3.6 mg/ml. His, Asn, Thr and Gln have a negative effect on solubility near the pI compared to Ala, a surprising result. Similar results were obtained compared to Ala when Arg and Lys were used. Smaller side chains, Asp and Ser, at position 76 increased the solubility over Ala.
F3. Hydrogen Bonding
Linus Pauling first suggested that H bonds (between water and the protein and within the protein itself) would play a dominant role in protein folding and stability. It would seem to make sense since amino acids are dipolar and secondary structure is common. Remember, however, the H bonds would be found not only in the native state but also in the denatured state. Do they contribute differently to the stability of the D vs N states? Many experimental and theoretical studies have been performed investigating helix <===> (random) coil transitions in small peptides. Remember all the intrachain H bonds in the helix? Are they collectively more stable than H bonds between water and the peptide in a (random) coil?
In thinking about conformational studies involving small peptides, it is useful to apply Le Chatelier's Principle to the equilibrium below:
random coil <==> helix
Anything perturbant (small molecules, solvent, etc) that would preferentially interact with the helical form would push the equilibrium to the helical form.
Early models assumed that intrachain H bonds were energetically (enthalpically) more favorable than H bonds between peptide and water. But to form a hydrogen bond requires an entropy payback since a helix is much more ordered (lower entropy) than a random coil (higher entropy). At low temperature, enthalpy predominates and helix formation in solution is favored. At high temperature, the helix is disfavored entropically. Imagine the increased vibrational and rotational states permitted to the atoms at higher temperatures. (Remember the trans to gauche conformational changes in the acyl chains of double chain amphiphiles as the temperature increased, leading to a transition from a gel to liquid crystalline phase in bilayer vesicles.) Theoretical studies on helix-coil transitions predict the following:
- as the chain length increases, the helix gets more stable;
- increasing the charge on the molecule destabilizes the helix, since the coil, compared to the more compact helix, has a lower charge density;
- solvents that protonate the carbonyl oxygen (like formic acid) destabilizes the helix; and
- solvents that form strong H bonds compete with the peptide and destabilize the helix. In contrast, solvents such as CHCl3 and dimethylformamide (a nonprotic solvent), stabilize the helix. Likewise 2-chloroethanol and trifluoroethanol, which form none or weaker H bonds to the peptide than does water, stabilizes the helix. (In the case of trifluoroethanol, molecular dynamics simulations have shown that TFE preferentially inteacts with (solvates) the peptide, which inhibits H bonds from the peptide backbone to water, stabilizing the intrahelical H bonds.
These helix-coil studies suggest that H bonds are important in stabilizing a protein.
But do they really? Why should these H bonds differ from those in water? It's difficult to figure out whether they are since there are so many possible H bonds (between protein and water, water and water, and protein and protein), and their strength depends on their orientation and the dielectric constant of the medium in which they are located.
If intrachain H bonds in a protein are not that much different in energy than intermolecular H bonds between the protein and water, and given that proteins are marginally stable at physiological temperatures, then it follows that the folded state must contain about as many intramolecular hydrogen bonds within the protein as possible intermolecular H bonds between the protein and water, otherwise the protein would unfold.
To resolve this issue, and determine the relative strength of H bonds between the varying possible donors and acceptors, many studies have been conducted to compare the energy of H bonds between small molecules in water with the energy of H bonds between the same small molecules but in a nonpolar solvent. The rationale goes like this. If the interior of a protein is more nonpolar than water (lower dielectric constant than water), then intrastrand H bonds in a protein might be modeled by looking at the H bonds between small molecules in nonpolar solvents and asking the question, is the free energy change for the following process < 0:
Dw + Aw <=======> (DA)n, DGo, K
where D is a hydrogen bond donor (like NH) and A is a hydrogen bond acceptor, (like C=O), w is water (i.e. donor and acceptor are in water), and n is a nonpolar solvent, and DGo and K are the standard free energy change and the equilibrium constant, respectively, for the formation of a H-bond in a nonpolar solvent from a donor and acceptor in water. This reaction simulates H-bond contributions to protein folding, where a buried H-bond is mimicked by a H-bond in a nonpolar solvent. The reaction written above is really a thought experiment, since it would be hard to set up the necessary conditions to make the measurement. However, we can calculate the DGo for this reaction since it is a state function and it really doesn't matter how one accomplishes this process.
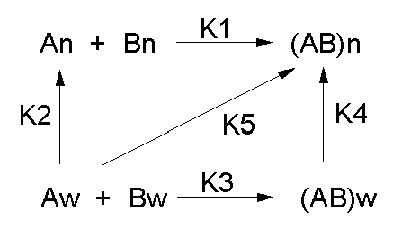
Let's consider a specific example: the formation of H bonds between two molecules of N-methylacetamide (NMA) in water and in a nonpolar solvent. The reaction scheme shown below describes a set of reactions (a thermodynamic cycle) involving the formation of H-bonded dimers of NMA . A and B are both molecules of NMA, in either water (w) or a nonpolar solvent (n).
N-methylacetamide is a good mimic for the H bond donors and acceptors of the peptide bond of a polypeptide chain.
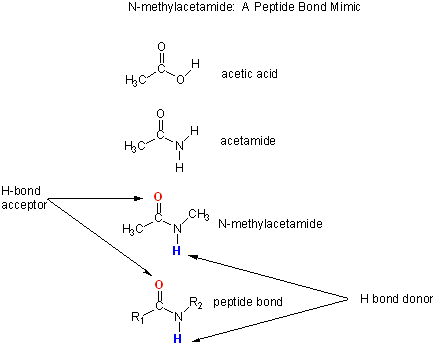
In the reaction scheme shown above,
K1 is the equilibrium constant for the dimerization of NMA in a nonpolar medium. This can be readily determined, and is >1, implying that DGo < 0. (Remember, DGo = -RTlnKeq) For the dimerization of NMA in CCl4, DGo1 = -2.4 kcal/mol.
K2 is the equilibrium constant (think of it as a partition coefficient) for the transfer of two NMA molecules from water to a nonpolar solvent (again easily measurable). For NMA transferring from water to CCl4, DGo2 = + 6.12 kcal/mol.
K3 is the equilibrium constant for the dimerization of NMA in water. This can be readily determined, and is <1, implying that DGo > 0. For the dimerization of NMA in water, DGo3 = +3.1 kcal/mol.
K4 is the equilibrium constant (think of it as a partition coefficient) for the transfer of a hydrogen-bonded dimer of NMA from water to a nonpolar solvent. You try to think of a way to measure that! I can't. This is where thermodynamic cycles comes in so nicely. You don't have to measure it. You can calculate it from K1-3 since DGo is a state function!
DGo2 + DGo1 = DGo3 + DGo4 OR -RTlnK2 + -RTlnK1 = -RTlnK3 + -RTlnK4
lnK2 + lnK1 = lnK3 + lnK4 = ln(K2K1 )= ln(K3K4) or (K2K1 )= (K3K4)
For NMA transferring from water to CCl4, D Go4 = + 0.62 kcal/mol.
(Note: Biochemists like to talk about thermodynamic cycles which may seem new to you. However, believe it or not, you have seen them before - in General Chemistry - in the form of Hess's Law!)
From K1-4and the corresponding DGo
values, we can now calculate DGo5
for the formation of H-bonded NMA dimers in a
nonpolar solvent from two molecules of NMA(aq). This reaction, which
we hope simulates formation of buried intrachain H bonds in proteins on
protein folding, is:,
Dw + Aw <=======> (DA)n, for which DGo5=
+3.72 (i.e. disfavored).
If this model is a good mimic for studying H bond formation on protein folding, it suggests that the formation of buried H bonds during protein folding does not drive protein folding.
However, if the transfer of D and A (from a large protein) from water to the nonpolar medium (modeled by K2) is driven by other forces (such as the hydrophobic effect), the positive value of K1 will strongly favored buried H bond formation. So, if this happens in proteins, it is clear why so many intrachain H bonds occur, since K1 is so favored. H bonds may not assist the collapse of a protein, but would favor internal organization within a compact protein. That is, H bonds don't drive protein folding per se, but form so that the folded protein would not be destabilized by too many unsatisfied H bonds.
There are potential problems with this simple model. The interior of a protein is not homogeneous (i.e. the effective dielectric within the protein will vary). H bond strength is also very sensitive to geometry. Also, there are many H bonds within a protein, so slight errors in the estimation of H bond strength would lead to large errors in determination of protein stability.
Another argument against H bonds being the determining factor in protein folding and stability comes from solvent denaturation studies. If intrachain H bonds are so important, then should not solvents that can H bond to the backbone denature the protein? Shouldn't water (55 M) act as a denaturant? It doesn't, however. Dioxane (5 member heterocyclic ring with O) which has only a H bond acceptor wouldn't be expected to denature proteins, but it does. H bonds also increase in nonpolar solvents. Peptides which have random structures in water can be induced to form helices when placed in alcohol solutions (trifluorethanol, for example), which are more nonpolar than water, as explained above in the helix-coil studies. If H bonds are the dominate factor in protein stability, the alcohols would stabilize proteins. At low concentrations of alcohol, proteins are destabilized.
Hence, based on small molecule studies and the study of protein in various cosolvents, it is unlikely that H bonds are the big stabilizers of protein structure. Only 11% of all C=O's and 12% of all NH's in protein have no H bonds (determined by analysis of X ray crystallographic structures). Of all H bonds to C=O, 43% are to water, 11% to side chains, and 46% to main chain NH's. Of all H bonds to NH, 21% are to water, 11% to side chains, and 68% to the main chain C=O. We will see later, however, than an opposite conclusion is reached from studies using site-specific mutagenesis.
F4. Hydrophobic Interactions: Introduction
We have studied the role of the hydrophobic effect (involving the favorable entropic release of caged water molecules about solvent-exposed hydrophobic groups) in driving micelle and bilayer formation. Does this also drive protein folding? To explore this questions, we will study the thermodynamics of small nonpolar molecules, especially benzene, with water and ask whether the thermodynamic parameter associated with benzene solubility are similar to those associated with protein stability. If this analogy holds, anything that will promote benzene solubility will lead to increased hydrophobic amino acid side chain exposure to water and hence protein denaturation. What is the evidence to support this?
a. crystal structures: These structures show that most nonpolar side chains are buried inside a protein, which is tightly packed and which excludes water. Studies show that as the surface area of amino acid side chains increase, the free energy of transfer of amino acids from water to ethanol becomes more negative.
Figure: Transfer of amino acids from water
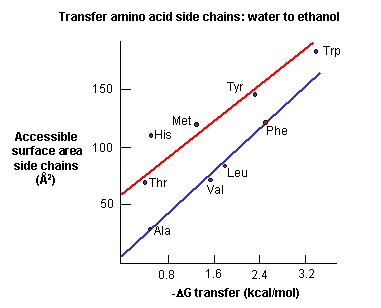
(Review free energies of transfer of hydrophobic groups in Chapter 1E: Lipids in Water - Thermodynamics )
b. low temperature denaturation of proteins - It has been observed that proteins can denature at low temperatures (less than 0oC), suggesting that nonpolar residues become more "soluble" in water at low temperatures (i.e. they move from the more hydrophobic interior of a protein to the more polar outside). Compare the solubility of nonpolar gases like CO2 or N2, which are more soluble at low temperature. As you heat solutions of nonpolar gases in water, the gases become less soluble as evidenced by bubble formation (i.e. phase separation of dissolved gases as they become more insoluble). If protein behavior is governed by this same behavior (greater solubility of nonpolar groups at low temperatures), it would suggest that proteins might denature at low temperatures (leading to increased exposure to water of the nonpolar side chains). This phenomena has been observed.
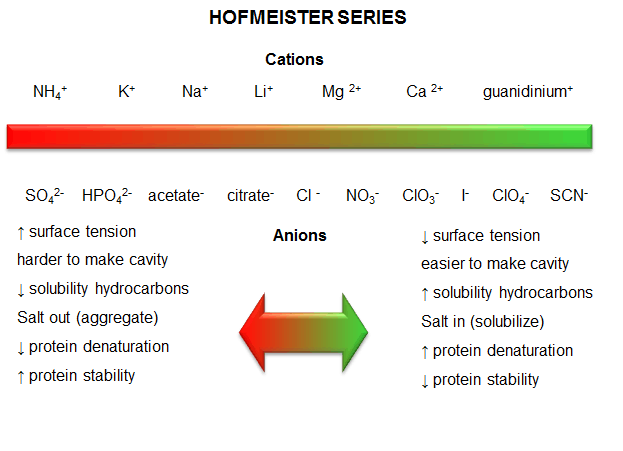
c. protein stability affected by different salt species - Over 100 years ago, Hofmeister determined the effectiveness of different cations and anions of salts to precipitate blood serum proteins in the 0.01 - 1 M concentration ranges. The series is shown below:
Cations: NH4+ > K+ > Na+ > Li+ > Mg2+ > Ca2+ > guanidinium
Anions: SO42- > HPO42- > acetate > citrate > Cl- > NO3- > ClO3- > I- > ClO4- > SCN-
- A salt from pairs of the first ions in these series (for example, (NH4)2SO4), when added to aqueous solutions of proteins, precipitate the native form of the protein. We must account for the fact that it precipitates the protein, and that the protein is precipitated in the native, not denatured state. More on why it precipitates proteins in a moment. The first ion in each series increases the surface tension of water (making it harder to make a cavity in the water to fit the nonpolar molecule). This decreases the solubility of nonpolar molecules. These "salt-out" nonpolar molecules, promoting not dissolution in water but aggregation followed by a phase separation. By analogy, they will stabilize the native state since the buried hydrophobic side chains would have a decreased propensity to move out into the aqueous environment.
- The last ions of the series have less affect on surface tension, and hence increase the solubility of nonpolar molecules ("salt-in"). By analogy, they will destabilize the native state since the buried hydrophobic side chains would have an increased propensity to move out into the aqueous environment.
- Hofmeister Series
Figure: Hofmeister Series
The solubility of benzene in aqueous salt solutions of this series increases from left to right, just as native protein stability decreases from left to right (i.e. the protein's nonpolar core residues become more "soluble" in water, leading to its denaturation).
d. conservation of hydrophobic core residues - These residues are highly conserved and correlated with structure.
e. Urea denatures proteins - Another additive, urea, at high concentrations is often used to denature proteins. People used to think that urea competed with the intrachain H bonds and hence unraveled the protein. The arguments above with H bonds disputes this contention since water should then denature protein. How does urea denature proteins? It has been shown that the free energy of transfer of the nonpolar amino acids into 8M urea is increasing negative as the side chains become bigger and more nonpolar.
Figure: Free energy of transfer of the nonpolar amino acids into 8 M urea
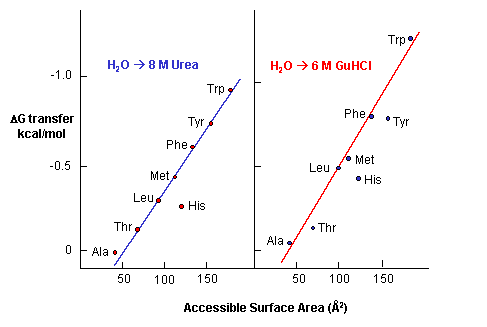
This is also true for denaturation by guanidine hydrochloride. Urea also increases the solubility of nonpolar molecules in a manner proportional to their surface area.
F5. Additives and Their Interactions with Protein Surfaces
Additives to proteins that increase the stability of the folded state of the protein also tend to decrease their solubilities. These additives are excluded from the preferential water hydration sphere around the protein (negative binding of these agents). Denaturants in contrast tend to increase protein solubility and interact preferentially with the protein surface. In their presence, proteins respond by increasing their surface area by denaturation. For stabilizers, proteins try to minimize their surface area by staying "native" and aggregating to form a precipitate, both of which minimizes the surface area from which the stabilizing agent is excluded.
The main effect of dissolved ions on water structure has been thought to involve changes in H bonds (either enhancers/structure maker or inhibitors/structure breakers) which correlate with salting-in or salting-out effects of various ions. Many techniques have been used to study these interactions:
- viscosity: inferential information on structure
- diffraction (x-rays/neutrons): gives information on coordination number of solvation shell (static information)
- NMR: information on average relaxation of bulk and hydration sphere water around ions (dynamic information)
- molecular dynamics simulations: which gives insight into short but not long range interactions between ions and water.
Recent studies have provided conflicting support for the notion of structure makers/breakers. Omta et al. 2003 have used femtosecond mid-infrared pump-probe spectroscopy to study actual H-bonds between water molecules in salt solutions (Mg(ClO4)2, NaClO4, and Na2SO4). In pump-probe spectroscopy, a sample is excited with a short pulse (pump) and after a short time lag, with another pulse (probe), which interacts with the excited state. The linear-polarized infrared pulses (pump) were used to excite OH groups in solution, followed by a probe pulse which was polarized 45 degrees compared to the pump pulse. Only those excited OH groups that had rotated in the time interval between the pump and probe would be excited by the probe. Using this technique, the time frame for reorientation of the OH groups, which is related to the "stiffness" of the H bonds, can be determined. The salts had no effect on the rotational motion of bulk water outside of the the first hydration shell, which suggests that salts have no effects on the H bond networks in bulk water. Mg2+ ions are considered structure making, as the ions greatly increases the viscosity of water, brought about supposedly by increased H bonds among water molecules. This study does not support this model. Increased viscosity of Mg solutions must be attributed to those ions directly interacting with water molecules. The solution can be modeled as bulk water with small rigid spheres of ion + first hydration sphere. Clearly, much more experimental and theoretical work must be performed to gain structure insight into the role of salts on water structure. Until then, we will continue to try to understand the effects of different salt on water structure in descriptive term and with use of thermodynamic quantities.
Studies have shown that urea binds preferentially to the protein surface, and hence tends to increase the protein's surface area and hydrophobic exposure, and denature proteins. However, note in the figure below, that glycerol, a bigger polar but uncharged molecule, stabilizes the native state. This pair of uncharged additives have correspondingly similar effects on protein stability as do the charged guanidine HCl/ammonium sulfate pair.
Figure: How reagents might interact with the surface of the protein.
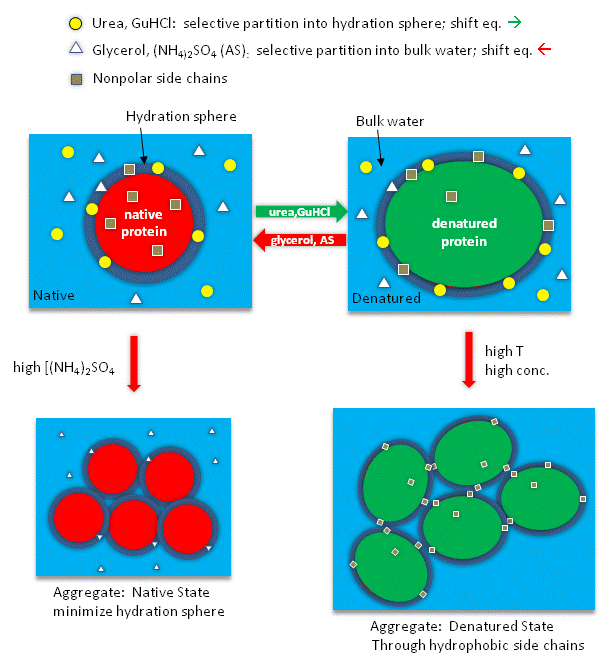
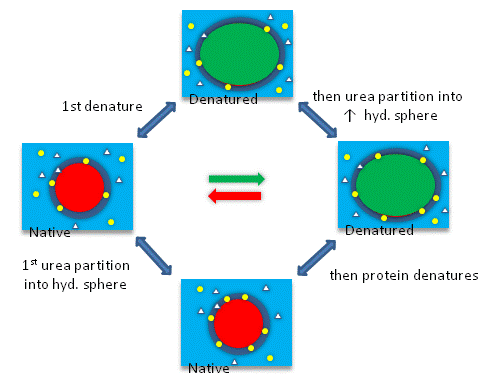
The next figures show such a thermodynamic cycle for urea denaturation of proteins
Figure: Thermodynamic cycle for urea denaturation of proteins
A graphical understanding of the type of sufrace changes that result from protein denaturation is given below.
Figure: Water Accessible Surface Area in Protein Unfolding
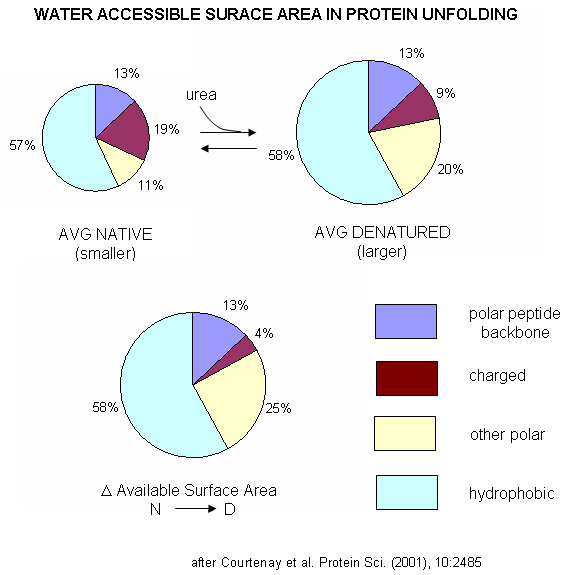
We will be discussing equilibria and how they may be shifted throughout this text.
A more detailed explanation of surface effects
and additives Courtenay, Capp, and Record (2001) used vapor phase osmometry to determine solution osmolality (Osm) and in turn preferential interaction coefficients (DGm3), from which KP values could be determined, using the formulas below, where a3 is the activity of component 3 - solute - in solution. (1 is solvent, 2 is protein, 3 is solute.) For example m1 = molality of bulk water = 55.5 mol/kg and b1 is the biopolymer hydration per square angstrom.. DGo obs = -RTlnKobs -(1/RT) DGo obs = lnKobs -(1/RT)( MDGo obs/Mlna3)T,P = MlnKobs/Mlna3) = DGm3 = (Mm3 /Mm2)T,P,m3 and DGm3 = (m3bulk(KP -1) b1 ASA)/m1 Using BSA as a protein solute, they
tested three destabilizers of native proteins: urea, guanidinium
HCl, and guanidinium thiocyanate. Graphs of osmolaity vs
destabilizer concentration (m3) showed almost linear increases in
both the presence and absence of BSA, but with lines that crossed
for the guanidium salts (lower osmolality in presence of BSA), which
indicated strong protein:solute interaction. Next, they determined, using vapor phase osmometry, the preferential interaction coefficients (from which KP values could be calculated) for BSA in the presence of increasing molal concentration (m3) of destabilizers. The values were always positive and increased with m3. KP values for the native protein were calculated to be 1.00 for KCl (control), 1.10 for urea, 1.30 for GuHCl, and 2.0 for GuSCN. For urea, previous calculations by the group showed the KP for urea and denatured proteins was the same as for native protein (1.10). Since it preferentially prefers to partition into the hydration sphere, and there is more hydration sphere in the larger denatured protein, urea drives protein unfolding. Using the guanidinium pair, they could resolve the KP values into that for the cation (GuH+) and the anion. For BSA, KP for GuH+ = 1.60 and 2.4 for thiocyanate. Similar calculations could be made of KP for the denatured state of BSA. The values for GuHCl and GuH+ were 1.16 (compared to 1.30 for the native protein) and 1.32 (compared to 1.60 for the native protein). Why does urea preferentially partition equally into the hydration spheres of native and denatured proteins, but GuHCl and GuH+ partitioned more into the native state? (Note however, that Kp for both N and D states were positive, leading to protein denaturation as with urea since the surface area and amount of hydration sphere greatly increases in the denatured state. ) Urea appears to partition selectively into the region near the peptide backbone and not charged or nonpolar surfaces. Theoretical and experimental work show that they are a constant percentage (13%) of the surface of a protein, whether in the native or denatured state, is composed of the peptide backbone. This make intuitive sense since the backbone extends over the entire length of the protein. However, the % of the surface with charged side chains decreases in the denatured state since then number of charged and polar side chains are a small fraction of the entire polypeptide backbone. The lower distribution of GuHCl and GuH+ into the hydration shell of denatured BSA can be accounted for by different distributions of surface polar and charged groups in the native and denatured state as shown in the figure below. For example, the percentage of charged groups on the surface of native vs denatured BSA is 29% vs 4%. It appears that GuHCl partitions into the hydration sphere near the peptide backbone and charged side chains. Urea appears to partition selectively into the region near the peptide backbone and not charged or nonpolar surfaces. This work gives a possible theoretical underpinning to the qualitative effects summarized in the Hofmeister series.
|
F6. The Hydrophobic Effect and Change in Heat Capacity
Our understanding of hydrophobic interactions has changed dramatically in the last several years. This is not reflected in most textbooks. The hydrophobic effect mean different things to different people. Some refer to the transfer of nonpolar solutes/solvents to aqueous solution. Some refer to the same phenomena only if the effects have a unique temperature dependency. Other refer to the ordering of water around nonpolar residues. The most recent explanation centers around the unique temperature dependencies of the transfer reactions. Before we can understand it, here is an interesting bit of data. If you dissolve one mole of methane in hexane, the volume of 1 L of hexane changes 60 ml, but if done in water, the water volume changes 37 ml, indicating that water molecules pack more efficiently around nonpolar molecules then in its absence.
Let's now consider the thermodynamic aspects of the hydrophobic effect, as we did for micelle and bilayer formation. In a brief summary, we found the the free energy of transfer of an amphiphile from aqueous solution into a micelle, for example, was disfavored enthalpically (unexpectedly) but favored entropically (also unexpectedly until we included solvent in our model). These experiments were done at one temperature and gave us our first initial understanding of the hydrophobic effect. We will expand on this view by looking at the enthalpic and entropic contribution to the transfer of benzene into water as a function of temperature. This will lead us to a more modern view of the hydrophobic effect.
THERMODYNAMICS OF MIXING TWO SUBSTANCES
If you mix two substances A and B that aren't very soluble in each other, two opposing forces are relevant.
- The tendency to mix is driven by an increase in entropy.
- The mixing is usually opposed by enthalpy.
The later makes "intuitive" sense since you might expect that van der Waal forces between A-B might be less than those of A-A and B-B (i.e. the old adage "like dissolves like"). If AA and BB self interactions are stronger, A would not dissolve in B and vice/versa. You would also expect no significant changes in entropy and enthalpy as a function of temperature in this ideal mixing. See the graph below.
The most modern understanding of the hydrophobic interactions shows that we have mixing of A and B, but with a unique temperature dependency for the value of the change in entropy and enthalpies. At room temperature, if one corrects the entropy changes for effects due just to mixing, the "excess" entropy is what principally opposes taking a nonpolar molecule into water. Enthalpy changes are small. We have modeled this effecting using structured water around the nonpolar residues. Remember our discussions of micelle and liposome formation? We will further our understanding of the hydrophobic effect by studying benzene solubility in water.
TRANSFER OF BENZENE TO WATER AS A FUNCTION OF TEMPERATURE: A MODEL SYSTEM
Before we discus entropy and enthalpy changes accompanying protein folding/unfolding, let's try to learn about the thermodynamic aspects governing benzene solubility in water. What happens to benzene solubility in water and the corresponding thermodynamic parameters as you raise the temperature? The graph below shows the change in G, H and -TS for taking benzene from pure benzene to water. This is real data.
Figure: change in G, H and -TS for taking benzene from pure benzene to water.

Notice the temperature dependency of these thermodynamic variables. As temperature increases, -TDS becomes more negative and hence drives benzene into water. (Remember D G = D H - TDS.) This seems to contradict our understanding of entropy effects in micelle and bilayer formation that we learned earlier when the DS > 0. Those studies on micelle and bilayer formation were done at one temperature. What about the structuring of water around the nonpolar group (decreasing the number of available microstates) hindering the process? Rationalize it this way. As the temperature is raised, available positional and thermal entropy of water increase significantly. It would seem logical that to then put a nonpolar residue into this system of water would become easier than putting it into more structure water (characterized by fewer microstates and lower positional and thermal entropy) at a lower temperature! (Remember from our review of thermodynamics that If the Tsurr is high, a given heat transfer to or from the surroundings will have a smaller effect on the ΔSsurr; conversely, if the Tsurr is low, the effect on ΔSsurr will be greater. Atkins, in his recent General Chemistry, uses the analogy of the effect of a sneeze in library compared to in a crowded street; The new American Chemistry General Chemistry text uses the analogy of giving $5 to a friend with $1000 compared to one who has just $10.)
But look at the other temperature anomaly. It becomes increasingly difficult from an enthalpic point of view to put benzene in water. We saw with micelle experiments that putting a hydrophobe into a micelle was disfavored enthalpically (and hence favored enthalpically to put it into water). At a high temperature, -TDS becomes zero, and their is no entropic barrier to putting benzene into water. The barrier is completely enthalpic. This is why a more nuanced definition of the hydrophobic effect has emerged.
If you sum DH and -TDS at each temperature, you get the curve shown for the total DG to take benzene from pure benzene to water. Notice that it is always positive, so it is always disfavored. The DG function is curved. It increases at low temperatures, and decreases at very high temperatures, implying that there will be a temperature at which there is a minimum solubility of benzene in water (a maximum in the positive DG). The minimum solubility of benzene (the max. positive DG) occurs when dG/dT = 0. Now remember from physical chemistry that
dG = VdP - SdT, so that dG/dT = V dP/dT - S = -S.
Therefore, dG/dT = 0 occurs when S = 0, and the maximum aversion is driven by enthalpy. This is at variance with the view that water ordering is the principal feature of the aversion of nonpolar residues for water.
Derivation for dG=VdP-SdT (for just PV work)

Let's review some more thermodynamics that the physical chemists in the crowd should remember. Even General Chemistry students should to a degree (a pun). (Molar) heat capacity, Cp, is defined as the heat required to raise the temperature of a mole of a substance 1oC. It has units of kJ (or kcal)/o mol. Look at the slope of the enthalpy curve as a function of temperature. It has units of kJ/o mol or of heat capacity and is given by:
Cp = dH/dT.
(Earlier, we studied Cp vs T curves for the phases transitions of water and for the gel/liquid crystalline phase transitions of phospholipid vesicles
Figure: Phase transitions of water

Figure: gel/liquid crystalline phase transitions of phospholipid vesicles
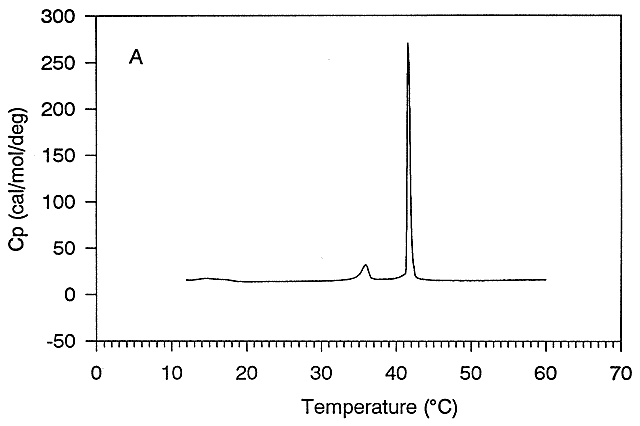
Figure: Thermal Denaturation of a protein using differential scanning calorimetry

Here is yet another equation for heat capacity that you derived in physical chemistry:
Cp = dH/dT= TdS/dT.
The last equality stems from Maxwell's relationships which Physical Chemistry students should remember. By analogy,
DCp = d(DH)/dT = Td(DS)/dT
which is POSITIVE in the benzene graphs above. THIS POSITIVE DCp OBSERVED WHEN A HYDROPHOBIC GROUP IS TRANSFERRED TO WATER IS THE SIGNATURE FOR OUR NEW DEFINITION OF THE HYDROPHOBIC EFFECT!
A positive DCp occurs when DH and DS are dependent on temperature, which is observed when a hydrophobe is transfer from a more nonpolar environment to water. Likewise, a negative DCp is observed when hydrophobes in water are transferred to a more nonpolar environment. Look at the graph showing the heat capacity of proteins vs temperature obtained using differential scanning calorimetry, as we previously studied with lipids.
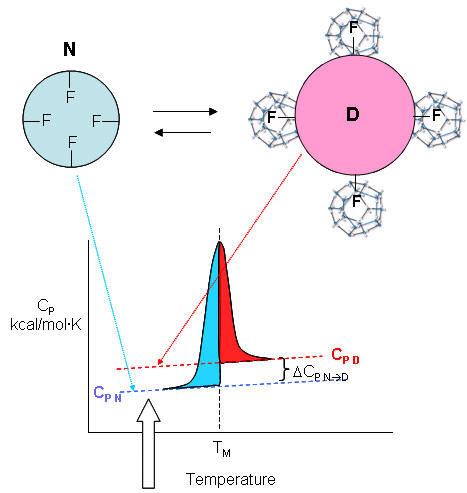
Figure: heat capacity of proteins vs temperature
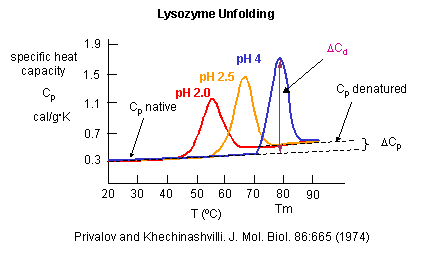
As the protein is heated, it reaches a temperature at which a large amount of heat is suddenly absorbed, as the protein unfolds. The area under the curve represents the heat absorbed on denaturation. The temperature at the midpoint is the Tm of the protein. (Why would the Tm be dependent on the pH of the solution?) Notice that there are two DCp's evident. One I will call DCd is associated with the actual denaturation process and is analogous to the change in heat capacity observed in phase changes, such as solid to liquid water. The other is D Cp which is the difference in heat capacity between the denaturated and native state. As was the case for the transfer of benzene to water, the DCp for protein denaturation is also positive, suggesting that in protein denaturation, hydrophobes are transferred from the interior of the protein to water.
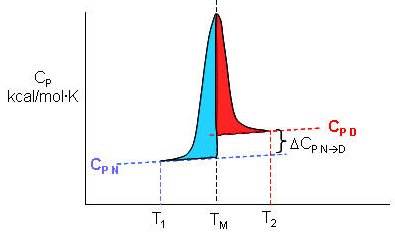
Figure: Determination of DH for Protein Denaturation by Differential Scanning Calorimetry
The following equations can be derived to help calculate the calorimetric enthalpy changes (DHcal = DHd) of denaturation from differential scanning calorimetry.
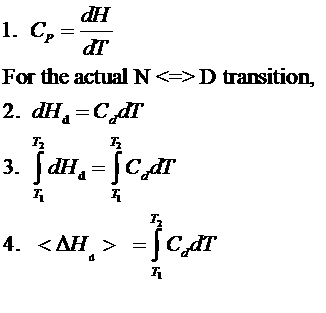
where <DHd> is the average enthalpy change that occurs on denaturation which is represented by the blue and red shaded areas in the curve above (between T1 and T2). Compare this to the van't Hoff enthalpy discussed in Laboratory Determination of DGo for Protein Folding/Unfolding.
For the calorimetric determination of DCd and DHd, the values are temperature dependent, and no assumption about the temperature independence need be made, as in the case of the DHvhoft .
What is the molecular basis for this large heat capacity change of transfer for benzene. One can show that the Cp is also proportional to the surface area of the nonpolar solute. At room temperature, water molecules surrounding the nonpolar residue are low in energy (lots of H bonds) and low in entropy (thermal and positional , fewer available microstates). As the temperature is raised, water populates higher energy states (fewer H bonds) and higher entropy (thermal and positional , more available microstates. The increase in temperature causes "melting" of surrounding water structure in so far as energy and entropy are concerned. The two different energetic states of water provide an energy storage mechanism.
Consider a slightly different explanation. Water molecules form an "iceberg"-like cage of water around nonpolar molecules, which is often called a clathrate. The water is fully H-bonded (to itself, not to the nonpolar molecule) in a fashion analogous to ice but the geometry of the H bonds is nonideal. This structuring of water decreases its entropy. With increasing temperature, the structured water "melts" which produces the large heat capacity of a solution of a nonpolar molecule in water, just as the actual melting of ice showed a large heat capacity. This large heat capacity is the signature thermodynamic features of the solution of a nonpolar molecule in water.
Heat capacity also had special significance in that
Cp = dH/dT = TdS/dT = -t2d2G/dT2
| A molecular interpretation of the "hydrophobic effect" It's still hard to get a good molecular interpretation of the meaning of DCp. The diagram below helps to directly relate the two. The smaller, more compact native state, with buried Phe (F) side chains denatures to the more open D state with exposed F side chains. Since these are nonpolar, we can envision a "clathrate" or cage of ordered water around them. I've extrapolated the heat capacity curves for both the native and denatured state into region where T < Tm (even though there is very little denatured state in that region). Now the "caged" water around the exposed F in the D state is low energy due to the "ice-like" H bond network. More heat would be absorbed (as the temperature is increased) to break up that cage compared to the same amount of heat applied to the N state. Hence, Cp D > Cp N. Is there a more quantitative description of the ordered water than a cage? Sharp et al investigated the "structure" of the caged water around nonpolar and polar molecules in a theoretical analysis supported by molecular dynamics (Monte Carlo) simulations. The average bond angles and lengths of water-water H bonds in the first hydration sphere around a nonpolar molecule like benzene decreased , but increased for polar ones such as potassium ions. The average changes noted arose from two types of H bonds compared to bulk water, those that were shorter and more linear, and those that were longer and more bent. They stated that "nonpolar groups do not so much increase the ordering of water as decrease the disordering".
A recent review by Silverstein suggests that an immobile clathrate cage is not a good representation for water surrounding a hydrophobe. Although we like to envision molecular models that allows us to "explain" experimental thermodynamic findings, such models themselves should be subjected to rigorous experimentation. An alternative explanation hinges on water's small size (compared to other solvents), its tight packing and high density. Consider the density of water compared to more nonpolar liquid solvents as seen the table below. Table: Density of common solvents
Let's consider the density of water surrounding an exposed nonpolar. If we envision the surrounding water as a clathrate, we might assume it is "ice" like. So what are the physical properties of ice and water than might give us insight into the water surrounding a nonpolar molecule? Ice, of course, has a lower density than liquid water. This can't be simply explained by the number of H bonds since experimental evidence shows that ice has an average of 4 H bonds per water molecule compared with liquid water, with an average of 2.4. Experimental data also shows that to accommodate water molecules into a rigid network of interacting waters with tetrahedral symmetry, the H-O-H bond angle increases to 106 from 104.5. Liquid water molecules, with fewer packing constraints, can self organize to maximize packing and hence macroscopic density. Studies suggests that ten water molecules solvate a buried methyl group and infrared studies show that four of these have significant barriers to rotational diffusion, suggest they are effectively immobilized and hence "ice-like". Silverstein suggests then that the water surrounding a nonpolar group on solution should be consider in a dynamic sense with some immobilized (as in ice) and the remaining more fluid-like. |
F7. Hydrophobic Effect and Protein Denaturation
The graph above shows a maximum in benzene insolubility. As the temperature is decreased from that maximum, benzene becomes more soluble in water. Alternatively, as temperature rises to that temperature of maximal insolubility, the solubility of benzene decreases (just like nonpolar gases become increasingly insoluble with increasing temperature). If you extrapolate the DG curve in this range of decreasing temperature past the range shown on the graph, it would cross the X axis and become <0, implying benzene would be favored to dissolve in water. Does the low temperature behavior of benzene/water interactions (becoming more soluble as the temperature is decreased from the maximum temperature for its insolubility) extend to and predict protein behavior at low temperature? (The following figures shows the analogy between benzene solubility in water and protein denaturation.
Figure: Analogy between benzene solubility in water and protein denaturation

In the figure, F stands for a Phe side chains, which can be buried, sequestered from water as it would be in the native state of the protein, and exposed to water, as it might be in the denatured state.) The answer is yes, at low temperature. The analogy to benzene being more soluble at low temperature is the hydrophobic side chains in a protein becoming more likely to flip into water, denaturing the protein. The low temperature behavior would predict low temperature protein denaturation. This phenomena has been observed. Note that it doesn't require a change to a state when the nonpolar side chains prefer to be in water. Just a change in that direction might be enough to tip the balance and lead to denaturation of the marginally stable protein. Please note that we are attempting to extrapolate the thermodynamic parameters associated with benzene solubility in water to the denaturation of a protein, NOT TO THE SOLUBILITY OF A PROTEIN IN WATER!
What about high temperature? Proteins denature as the temperature increases to the range that the DG curve for benzene reaches a peak. If the hydrophobic residues behave like benzene they would like to stay buried and not flip out into water as the temperature rises to the maximum in the DG curve. Hence this predicts that the protein should become more stable. What then explains the denaturation of proteins at high temperature? Another factor must account for it. What is it?
Remember the trans to gauche conformational changes in fatty acid residues in liposomes? As the temperature is increased, more conformations become available and occupied. Consider a protein. At low temperature, their is only one native state and to pick a number, maybe 100 accessible denatured states. At high temperature, there is still only one native state, but possibly 1000 accessible denatured states. More accurately, think of the protein existing in an ensemble of conformations. As the temperature increases, more denatured states can be populated, compared to at lower temperatures, leading to an entropic driving force favoring unfolding. Which way would the chain conformational entropy drive the protein at high temperature? Clearly, it would be driven to the most number of states - to the denatured state. Hence a modern definition of the hydrophobic effect can explain low temperature denaturation, but not high temperature denaturation.
Remember when we discussed the thermodynamics of transfer of aliphatic alcohols from water to the pure alcohol? We decided that DGo was < 0 (favorable), and that DHo > 0 (disfavorable) and DSo > 0 (favorable). Also remember that these figures were derived at one temperature. We were somewhat surprised that DHo > 0 since this implies that from an enthalpic point of view, the alcohol-water interactions, or the water-water interactions surrounding the hydrocarbon chain are more favorable than the alcohol-alcohol interactions or bulk water-water interactions. The freeing of structured water surrounding the aliphatic chain when the alcohol is transferred to the pure alcohol is the driving force for the reaction. What happens at different temperatures? I hope it makes intuitive sense that the entropy effects will change with temperature, as described above. Likewise it makes sense that the enthalpy would change. Hence DH and DS for the transfer of amphiphiles into water will be a function of temperature - i.e. the reaction proceeds with a DCp.
Web Links:
Online Literature:
K. A. Dill and J. L. MacCallum, The protein folding problem, 50 years on, Science 338, 1042-1046 (2012). (PDF) (Full Text Online) (podcast)
Southall, N.T., K.A. Dill, and A.D.J. Haymet. A View of the Hydrophobic Effect. Journal of Physical Chemistry B 106: 521-533 (2002). (PDF)
Summary of studies from small molecules (N-methyacetamide and benzene)It is clear that proteins are not all that stable, and many contributions of varying magnitudes must sum to give the proteins marginal stability under physiological conditions. Hydrophobic interaction, defined in the new sense, must play a major role in stability. Also, since proteins are so highly packed compared to a lose denatured state, London Forces must also play a significant part. (Remember dispersion forces are short range and become most significant under conditions of closest packing.) Opposing folding is the chain conformational entropy just described. Since proteins are so marginally stable, even one unpaired buried ionic side chain, or 1-2 unpaired buried H bond donors and acceptors in the protein may be enough to "unravel" the native structure, leading to the denatured state.
F8. Mutagenesis and Protein Stability
In the last decade, the contributions to the overall stability of a protein from the hydrophobic effect and H bonds has been studied using site specific mutagenesis. In this technique, the DNA coding sequence for a given amino acid in a gene can be altered so that the new mutant protein differs from the normal protein (often called the wild type protein) by one amino acid. To probe the hydrophobic effect, for example, a buried hydrophobic amino acid like Ile could be changed to Gly which is much smaller, and offers less hydrophobic contribution to the stability of the native state. The result of this mutation might leave a "hole" in the protein (not unlike the vacant holes in crystal structures of salts). This "hole" might be diminished in size by subtle rearrangement of the protein structure in the vicinity. Certain amino acids would not be used as replacements in such studies. For instance, an Ile would not be replaced with a positively charge Arg which would clearly destabilize the protein. The extent of destabilization in mutant proteins can be determined by calculating the DGo for the native to denatured transition using urea as the denaturing agent.
Previously, the following statistics were presented concerning the distribution of amino acids in the tertiary structure of a protein. New values are shown below in red, based on much more crystallographic data, as summarized in Pace's article.
- The side chain location varies with polarity. Nonpolar side chains, such as Val, Leu, Ile, Met, and Phe, are nearly always (83%) in the interior of the protein.
- Charged polar side chains are almost invariably on the surface of the protein. (54% - Asp, Glu, His, Arg, Lys are buried away from water, a bit startling!)
- Uncharged polar groups such as Ser, Thr, Asn, Gln, Tyr, and Trp are usually on the surface, but frequently in the interior. If they are inside, they are almost always H bonded (63% buried - Asn, Gln, Ser, Thr, Tyr, again startling) .
- Globular proteins are quite compact, with water excluded. The packing density (Vvdw/Vtot) is about 0.75, which is like the NaCl crystal and equals the closest packing density of 0.74. This compares to organic liquids, whose density is about 0.6-0.7.
Two articles by Pace suggests that Dills "influential review (from which much of the above derives) that concluded that hydrophobicity is the dominant force in protein folding" should be rethought. Using site specific mutagenesis to change Asn (which can H bond through its side chain) to Ala (which can't) in a variety of proteins, he has shown that approximately 80 cal/mol/A3 of stability is gained if a side chain (in this case Asn) can form buried H bonds to buried amide links of the protein backbone. Similar studies of mutants in which Leu is replaced with Ala, and Ile with Val, suggests that only 50 cal/mol/A3 is gained from burying a hydrophobic -CH2- methylene group. Extending these results to protein folding suggest that proteins stability is determined more by the formation of buried H bonds than by the hydrophobic effect.
The investigators measured DGo for the N <=> D transition (presumably by varying the urea concentration and extrapolating the DGo for unfolding to 0 M urea (see: Lab Determination of DGo of Unfolding). For the reaction as written, DGounfolding > 0 at room temperature and 0 M urea. The mutant protein, since they are destabilized, would have a less positive value for DGounfolding (They would also have a less negative value for folding since they are less stable). The difference in DGounfolding between the wild type and mutant (DDG) is expressed as:
DDG = DGounfolding wild-type - DGounfolding mutant > 0
DDG > 0 since DGounfolding wild-type > DGounfolding mutant. The more positive the DDG, the more the mutant is destabilized in comparison to the wild type. The data for a series of mutants is shown below.
Analysis of Mutants: H Bonds in Protein Folding
| mutation | DVol side chain (A3) | % buried | DDG (kcal/mol) (destabilized) |
DDG (cal/mol/A) (destabilized) |
| Asn to Ala | 37.4 | 95 | 2.9 | 78 |
| Leu to Ala | 74.5 | 99 | 3.6 | 48 |
| Ile to Val | 25.8 | 100 | 1.3 | 50 |
What leads to protein stabilization/destabilization when Asn is changed to Ala?
One possible contributor to stability is the side chain conformational entropy. Since in the mutant the Ala would find itself in a larger "hole" and have greater freedom for motion, it would have more conformational entropy that would stabilize the mutant over the wild type. Hence this effect can NOT explain the observed destabilization of the Asn to Ala mutant.
In the proteins he studied, only one of eight Asn to Ala mutation involved an Asn in a helix, so the average change could not be attributable to differences in helix propensities for the two amino acids.
In the mutants, assuming no rearrangement of the remaining side chains, there is an "unnecessary" and unoccupied 37.4 A3 cavity. To create this cavity is thermodynamically unfavorable (about 22 cal/mol/A3 obtained from values for hydrophobic mutations). If the same penalty were applied here, the Asn to Ala mutant would be destabilized by 0.8 kcal/mol (22 x 37.4), This is significantly less that the observed destabilization (2.9 kcal/mol), so this effect also could not account for the destabilization of the Asn to Ala mutants.
If there were compensatory changes to minimize the cavity size, this would only help to stabilize the protein and hence can not account for the observed destabilization.
Possible Explanation of Destabilization of Asn to Ala Mutants
| possible reasons | explanation | effect on mutant | support observed destab. of mutant? |
| residue conformational entropy | Ala in bigger hole: more freedom motion; favored entropically |
stabilize mutant | NO |
|
free energy change |
energy penalty to make an unoccupied cavity approx. 0. 8 kcal/mol
|
destabilize |
yes but of insufficient size compared to the observed effect (2.9 kcal/mol |
| free energy change protein conformational changes |
rearrange protein to fill cavity | stabilize mutant | NO |
Hence these alternative sources to explain the destabilization of the mutant can't account for the data and we're left with the explanation that the stability of the native protein over the mutant is accounted for by burying the H bond donor and acceptors of the amide group and associated changes in van der Waals interactions.
Pace argues that burying the amide group of Asn is similar to burying the peptide bond of the main chain. There sizes are very comparable. Free amide groups can form four H bonds, but peptide (amide) groups can only form three. Even if the value of 78 for the DDG (cal/mol/A) is adjusted for this, the new value of 62 is still larger than that for burying a methylene group. Analysis of 108 folded proteins has shown that hydrophobic groups contribute 118,200 A3 of buried volume, compared to 92,000 A3 for peptide groups. Multiplying these figures by 78 and 49 (from the above table) suggests that overall, burying peptide groups contributes more to protein stability than burying hydrophobic groups.
Would electrostatic interactions of the buried peptide group with the surrounding environment destabilize a protein? Pace argues that this would be more than compensated for by favorable van der Waal's interactions (short range) at the buried site. This can be illustrate by comparing the DG transfer of an amide from water to the vapor (11.2 kcal/mol)) compared from water to cyclohexane (7.6 kcal/mol). Transfer to the vapor is more unfavored (due to the desolvation required when it moves to the gas phase) than to cyclohexane, even though a cavity must be created in the cyclohexane (a process which would be unfavored entropically). Transfer to octanol is even more favored (1.4 kcal/mol) but all these values are still positive (disfavored). Similar experiments with transfer of a methylene group (-CH2-) are negative, given the hydrophobic effect and the close packing van der Waal's interactions possible. These suggest that van der Waals interactions formed on burying an amide in any solvent are stabilizing. Now consider the packing density of atoms for various substances:
Packing Densities
| substance | packing density |
| water | 0.36 |
| cyclohexane | 0.44 |
| closest packed spheres | 0.71 |
| protein interiors | 0.75 |
From this table it should be apparent that van der Waals interactions (short range) will be more stabilizing in the interior of the protein compared to the same groups in bulk water (or in the denatured state). Carbonyl groups are more polarizable than methylene groups, which should contribute to van der Waals interactions.
One other addition. It has been noted that Gly peptides are not very soluble in water. The backbone, even with the polar peptide bonds appears to be solvophobic. If the backbone of any polymer can't interact well with the solvent - i.e. the solvent is "poor" - then the backbone interacts with itself, which drives collapse. If the backbone interacts well with a "good" solvent, it won't collapse as readily.
F9. Protein Stability and Molecular Orbitals
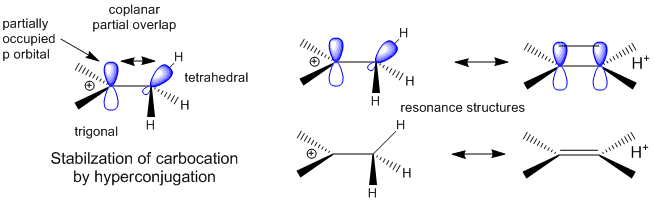
A more complete description of the energetics underlying protein structure and stability would involve quantum mechanical effects. These have not been studied in detail since quantum mechnanical calculations are difficult to perform on large molecules. Recent work has led an understanding of a new source of stability of proteins based on overlap of proximal molecular orbitals that stabilizes a protein through electron delocalization. Two common examples of electron delocalization that increase stability are resonance and hyperconjugation. Resonance involves delocalization of electrons through overlap of adjacent atomic p orbitals to form low energy molecular bonding orbitals. You may remember hyperconjugation being used to explain the relative stability of tertiary carbocations compared to secondary or primary ones. The typical explanation involves electron donation and pushing from the adjacent methyl groups which effectively decreases the charge on the carbocation. A more correct explanation involves overlap of molecular orbitals, specifically of a C-H s orbital from one of the C-H bonds of the methyl group with the partially filled p orbital on the carbon atom containing the charge as seen in the figure below.
Figure: Stabilization of Carbocations by Hyperconjugation
It should also not be surprising that orbital overlap accounts for hydrogen bonds interactions (in contrast to the more simplistic explanation of the attractions between the partial charges on hydrogen bond donors and acceptors). Bartlett et al (2010) have recently described two types of orbital overlaps involving electron delocalization that stabilize protein structures. Molecular orbital description show that two lone pairs on the oxygen (hydrogen bond donor) in amide bonds are different. One pair, ns (Figure a below) is in a nonbonding orbital with 60% s character, while the other, np (figure b below), has approximately 100% p character. Figure c below shows that a hydrogen bond between the carbonyl oxygen of the ith amino acid and the amide H of the ith+4 amino acid can be described in quantum mechanical terms as the overlap (i.e. delocalization) of the ns nonbonding orbital on oxygen and the s* antibonding N-H orbital. What about the np electrons on the carbonyl O? They found evidence for a new kind of stabilizing influence in proteins as the np orbital overlaps with the an antibonding p* orbital on the ith+1 carbonyl group (figure d below) when the two amino acids are proximal as parts of secondary structures, including alpha and 310 helices as well as in twisted b sheets.
Figure: Orbital involvement in H-bonds and n to pi* interactions in alpha helices

(a) s-rich lone pair of an amide oxygen. (b) p-rich lone pair of an amide oxygen. (c) ns to σ*: hydrogen bond in an a-helix. (d) np to p*: n to p* interaction in an a-helix. Reprinted by permission from Macmillan Publishers Ltd: Nature Chemical Biology. Bartlett, G. et al. n to pi* interactions in protein. 6, pg 615 (2010)
To test which phi-psi angles would allow close enough approach for np to p* interactions, the investigators performed quantum mechanical computations on possible conformations of AcAla4NHMe for which np to p* were possible (see figure A below). These calculations showed these interaction were possible for values of d ≤ 3.2 � and 99� ≤ θ ≤ 119� (figure a below). Distances less than 3.2 angstroms, van der Waals surfaces of the C and O on adjacent carbonyls overlap, suggesting that the interaction is quantum mechanical and not classically mediated. Next they calculated d and q values for on high resolution x-ray structures of known proteins. Red shading in the Ramachandran plot in figure c below phi/psi regions in actual proteins that meet the required geometry for np to p* overlap. Hence these geometry are abundant in proteins, especially in secondary structures described above.
Figure: Ramachandran plots of n to pi* interactions.
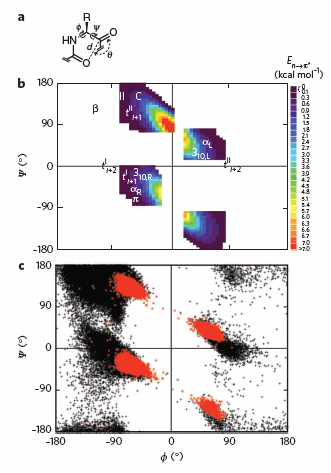
(a) Definitions of dihedral angles φ (C′i�1�Ni�Cα i�C′i) and ψ (Ni�Cαi�C′i�Ni+1), distance (d) and planar angle θ. Criteria for an n to p* interaction in the crystallographic analyses: d ≤ 3.2 �; 99� ≤ θ ≤ 119�. (b) Computational data showing the energy. Reprinted by permission from Macmillan Publishers Ltd: Nature Chemical Biology. Bartlett, G. et al. n to pi* interactions in protein. 6, pg 615 (2010)
F10. Protein Stability in Thermophilic Organisms
What kinds of modifications are made to the sequence of a protein as the temperature that the organism thrives increases? A recent study by Szilagyi and Zavodszky (Structure, 8, pg 493, 2000) studied 93 structures of 25 proteins, 29 from organisms that live at elevated temperatures (thermophiles, >50oC for optimal growth ) and 64 at nominal temperatures (mesophiles). Here are their results:
- the number of H-bonds and secondary structure elements do not correlate with temperature, but the number of salt bridges do.
- in hyperthermophiiles (>80oC for optimal growth organisms) that thrive at very high temperatures (100oC), few internal cavities were found.
- in those that thrive at intermediate high temperatures (45-80oC) the surface had more polar residues.
- generally there was an increase in weaker ion pairs (increased distance between the charged side chains) in the hot group, but increases in strong and weak ion-ion bonds in the very hot group.
Kashefi and Lovley recently reported the identification of a bacteria obtained from a hydrothermal vent in the northeastern Pacific ocean. In a laboratory setting, the strain grew in water at a temperature of 121oC under high pressure. These are the same conditions used in autoclaves to produce sterile samples. Cell doubling took place under these conditions in 24 hours. The authors suggest that this strain would be useful to determine molecules and their properties necessary for such high temperature growth.
Using a computational program called Rossetta Design (PNAS, 97, 10383 (2003)), Korkegian et al determined mutations in buried side chains of the homodimer cytosine deaminase. Buried residues are presumably are important in the stability of a protein and are targets for mutagenesis experiments that would increase the melting temperature (Tm) of the protein. In the program, a target sequence was "threaded" onto the sequence of the template protein (the wild type protein) and changes made to side chains in the random sequence. Energies were calculated and those changes resulting in lower energies were saved. Target residues (88) within 4 angstroms of the active site and the dimer interface were fixed to those in the wild-type template in order to minimize alterations in the catalytic activity of the enzyme, cytosine deaminase, that they chose to study. Remember, the goal of the study was not to increase the catalytic activity of the enzyme, but rather increase its themostability. The rest (65) were changed and energies calculated. 49% of the amino acids subjected to random change produced no change in amino acid compared to the template (wild-type) side chain. 16 changes on the surface were ignored. Two sets of changes were observed, one involving amino acids packed between an alpha helix and beta strands, and the other set between two alpha-helices. These later mutants, when prepared in the lab using recombinant DNA technology, were soluble at high protein concentrations, and could be studied. Three different mutants (A23L, I140L, V108I) were made which increased the TM by about 2 degrees. However, a triple mutation had TM values 10 degrees higher than the wild-type protein and a 30-fold longer T1/2 at 50 degrees C. When the triple mutant was introduced into bacteria, the bacteria grew better at higher temperatures. Crystal structures of both the wild-type and triple mutants shown essentially an identical fold, with about 70 A2 of additional surface area buried in the mutant protein.
Beeby et al. analyzed sequence and structural data from P. aerophilum (archea) and Thermus thermpilus (thermophilic bacteria) and found that disulfide bonds stabilized proteins from these species. Cytoplasmic protein from eukaryotes don't have disulfides due to the presence of reducing agents (such as glutathione) in the cell. In those thermophiles with disulfides in proteins, a novel protein, protein disulfide oxidoreductase, was found, which catalyzes the formation of sulfide bonds. Finally, Berezovsky and Shakhnovich have also analyzed proteins from hyperthermophilic archea and bacteria and compared them to analogous proteins from mesophilic bacteria. They found two types of stabilizations of hyperthermophilic proteins, depending on the evolutionary history of the organism. Proteins from cells that originally evolved in high temperature conditions (archea) were very compact (maximizing van der Waals interactions, had a high number of contacts per residue, and a high percentage of hydrophobic residues), but did not use specific structural stabilizing interactions (like electrostatic in salt bridges). In contrast, proteins from cells the originally evolved under mesophilic conditions, but later adapted to hyperthermophilic conditions had proteins that evolved specific sequences features that stabilized electrostatic interactions (more charged residues, salt bridges, .
F11. General Links and References
- Bartlett, G. et al. n to pi* interactions in protein. Nature Chemical Biology. 6, pg 615 (2010).
- Pace, C. et al. Protein Ionizable Groups: pK values and Their Contribution to Protein Stability and Solubility. J. Biol Chem. 284, 13285 (2009)
- Silverstein, T. Hydrophobic Effect: J. Chem Ed. 85. 917-918 (2008)
- Sharp, K. & Madan, B. Hydrophobic Effect, Water Structure, and Heat Capacity Changes. J. Phys.Chem. 101, 4343 (1997)
- Berezovsky, I & Shakhnovich, E. Physics and Evolution of Thermophilic Adaptation. PNAS 102, 12742 (2005)
- Beeby et al. The genomics of disulfide bonding and protein stabilization in themophiles. PLoS Biology. 3, 1549 (2005)
- Courtenay, E. et al. Thermodynamics of interactions of urea and guanidinium salts with protein surfaces: relationship between solute effects on protein processes and charges in water-accessible surface area. Protein Science. 10, 2485 (2001)
- Korkrgian, A. et al. Computational Thermostabilzation of an Enzyme. Science. 308, pg 857 (2005)
- Kashefi, K. and Lovley, D. Extending the Upper Temperature Limit for Life. Science. 301, pg 934 (2003).
- Omta et al. Negligible Effect of Ions on the Hydrogen-bond structure in liquid water. Science, g 347, 320 (2003)
- Dixit et al. Molecular degregation observed in a concentrated alcohol-water solution. Nature. 416, pg 829 (2002)
- Pace, C.N. Polar Group Burial Contributes More to Protein Stability than Nonpolar Group Burial. Biochemistry. 40, pg 310 (2001)
- Water at the Nanoscale (How water enters a hydrophobic nanotube - a molecular dynamics simulation) . Nature. 294414, pg 156, 188 (2001)
- Shortle & Ackerman. Persistence of Native-Like Topology in a Denatured Protein in 8 M Urea. Science. 293. pg 487 (2001)
- Brooks et al. Taking a Walk on a Landscape (about protein foldiing) Science, 293, pg 612 (2001)
- Chemistry Beyond the Molecule (supramolecular chemistry). Nature. 412, pg 397 (2001)
- Fernandez-Lopez et al. Rings of Destruction. (Cyclic peptides as drugs). Nature. 412 pg 392, 452 (2001)
- Scatena et al. Water at Hydrophobic Surfaces: Weak Hydrogren Bonding and Strong Orientation Effects. Science. 292. pg 908 (2001)
- Maritan et al. Best Packing in Proteins and DNA. Nature, 406, pg 251, 287 (2000)
- Oh et al. Folding-Driven synthesis of oligomers. Nature. 414, pg 889 (2001)
- Molecules at the Edge (solvent interactions at interfaces) Nature. 410, pg 645 (2001)
- Oesterhelt et al. Unraveling a membrane protein (denaturing a protein with atomic force microscopy). Science. 288, pg 63, 143 (2000)
- Sohl et al. Unfolded conformations of a-lytic protease are more stable that its native state. (has large kinetic barrier to unfolding). Nature. 395, pg 817 (1998)
- Pascher et al. Protein folding triggered by electron transfer. Science. 271, pg 1558 (1996)
- Koide et al. Design of a single-layer b-sheet without a hydrophobic core. Nature. 403, pg 456 (2000)
- Nelson et al. Solvophobically driven folding of nonbiological oligomers. Science. 277, pg 1793 (1997)
- Pace,C. N. et al. Forces contributing to the conformational stability of proteins. FASEB Jouranl. 10, 7583 (1996)
Navigation
Return to Biochemistry Online Table of Contents
Archived version of full Chapter 2F: Thermodynamics and IMFs of Protein Stability

Biochemistry Online by Henry Jakubowski is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.